Temas
Uma vez que já conhecemos a definição de vetor, vamos estudar algumas das operações básicas que podem ser realizadas com vetores.

Soma de vetores
Se temos dois vetores  e
e  ,então a soma de
,então a soma de  e
e  é:
é:

Em outras palavras, o vetor soma de  e
e  é o vetor que resulta da soma dos componentes correspondentes desses vetores: o primeiro componente de
é o vetor que resulta da soma dos componentes correspondentes desses vetores: o primeiro componente de  é somado ao primeiro componente de
é somado ao primeiro componente de  , e o segundo componente de
, e o segundo componente de  é somado ao segundo componente de
é somado ao segundo componente de  .
.
Interpretação geométrica da soma
Vamos observar a seguinte figura que mostra a soma dos vetores y
y  :
:
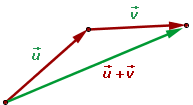
Se  e
e  ão dois vetores livres, então, para somá-los geometricamente, primeiro escolhe-se um representante de
ão dois vetores livres, então, para somá-los geometricamente, primeiro escolhe-se um representante de  cujo ponto inicial coincide com o ponto final de
cujo ponto inicial coincide com o ponto final de  . Logo,
. Logo,  é o vetor cujo ponto inicial é o de
é o vetor cujo ponto inicial é o de  e cujo ponto final é o de
e cujo ponto final é o de  .
.
Também podemos escolher um representante de  e modo que seu ponto inicial seja o ponto final de
e modo que seu ponto inicial seja o ponto final de  . A soma
. A soma  ] terá o mesmo valor, mas, neste caso, será obtida unindo-se o ponto inicial de
] terá o mesmo valor, mas, neste caso, será obtida unindo-se o ponto inicial de  ao ponto final de
ao ponto final de  .
.
Regra do paralelogramo
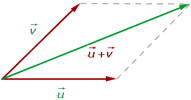
O que discutimos anteriormente como a soma geométrica dos vetores é conhecido como a regra do paralelogramo. Em particular, se quisermos somar dois vetores livres com a mesma origem, devemos traçar retas paralelas a esses vetores. Assim, obtemos um paralelogramo cuja diagonal - partindo da origem comum - representa a soma dos vetores.
Observa a figura abaixo que exemplifica a regra do paralelogramo.
Subtração de vetores
A subtração de dois vetores  e
e  é simplesmente a soma de
é simplesmente a soma de  com
com  (isto é, o oposto de
(isto é, o oposto de  ).
).
Dessa forma, considerando os componentes de  e
e  , assim, a subtração é dada por:
, assim, a subtração é dada por:

Geometricamente, a subtração de  e
e  é obtida do mesmo modo que a soma, com a única diferença de que somamos o oposto de
é obtida do mesmo modo que a soma, com a única diferença de que somamos o oposto de  . Observe a figura a seguir que mostra a
. Observe a figura a seguir que mostra a  e pode-se notar que no extremo de
e pode-se notar que no extremo de  é colocado a origem de
é colocado a origem de  .
.
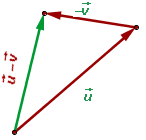
Observe que a subtração  graficamente é o vetor que une o ponto final de
graficamente é o vetor que une o ponto final de  ao ponto final de
ao ponto final de  .
.
Produto de vetor por escalar
A multiplicação de um vetor  por um número real
por um número real  é escrito
é escrito  ou
ou  . Esse número
. Esse número  é chamado de escalar. O produto de um vetor por um escalar é outro vetor que satisfaz as seguintes propriedades:
é chamado de escalar. O produto de um vetor por um escalar é outro vetor que satisfaz as seguintes propriedades:
 tem a mesma direção que
tem a mesma direção que  .
.- Se
 é positivo, então
é positivo, então  tem o mesmo sentido que
tem o mesmo sentido que  .
. - Se
 é negativo, então
é negativo, então  tem sentido contrário ao de
tem sentido contrário ao de  .
. - O módulo de
 é
é 
Observemos la siguiente figura que representa la multiplicación de  por 3.
por 3.

Em termos de componentes, se  ,, então o produto por escalar é dado por:
,, então o produto por escalar é dado por:

Exemplos de exercícios con vetores
Sejam os vetores  e
e  . Então:
. Então:
1 A soma é:

2 A subtração é:

3 O oposto de  é:
é:

4 O produto do vetor  por 3 é:
por 3 é:

Resumir com IA:












