Temas
Adição e subtração de frações
Com denominadores iguais
Somam-se ou subtraem-se os numeradores e mantém-se o denominador.
Com denominadores diferentes
Primeiramente, reduzimos os denominadores a um denominador comum e somamos ou subtraímos os numeradores das frações equivalentes obtidas.
Determina-se o denominador comum, que será o mínimo múltiplo comum (MMC) dos denominadores.
Esse denominador comum é dividido por cada um dos denominadores e o quociente obtido é multiplicado pelo numerador correspondente.
Somam-se ou subtraem-se os numeradores das frações equivalentes obtidas.
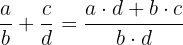
O MMC de 
. Uma forma simples de encontrá-lo é a seguinte:
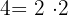
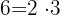
Assim, percebemos que, para ter o mesmo denominador, precisamos multiplicar a primeira fração por 
, e a segunda por 
, o que nos dá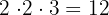 
.
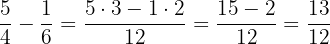
Multiplicação de frações
A multiplicação de duas frações resulta em outra fração, cujo numerador é o produto dos numeradores e o denominador é o produto dos denominadores.
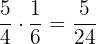
Divisão de frações
A divisão de duas frações resulta em outra fração, cujo numerador é o produto dos extremos e o denominador é o produto dos meios.
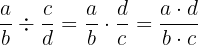
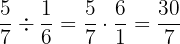
Operações combinadas e ordem de prioridade
1. Transformar os números mistos e decimais em frações.
2. Calcular potências e raízes.
3. Efetuar as operações dentro de parênteses, colchetes e chaves.
4. Realizar multiplicações e divisões.
5. Realizar adições e subtrações.
Exemplos de exercícios e problemas com frações
1. 
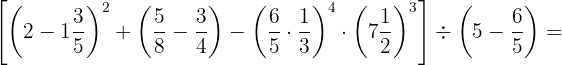
Primeiro fazemos as operações com os produtos e números mistos dentro dos parênteses.
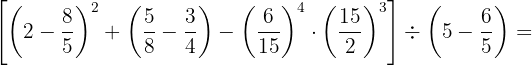
Depois, resolvemos o primeiro parêntese, eliminamos o segundo, simplificamos no terceiro e calculamos o último.
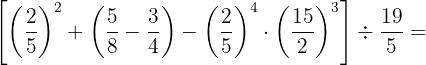
Calculamos o produto e simplificamos.
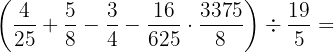
Como temos números grandes na adição do primeiro parêntese, resolvemos essa parte primeiro.
Dessa forma, temos:
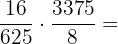
Antes de somar, simplificamos:
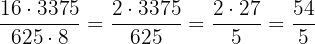
Realizamos as operações do parêntese:
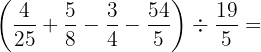
Vamos descobrir o MMC de 
:
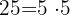
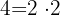
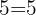
Percebemos que o MMC é 
.
Multiplicamos a primeira fração por 
, a segunda por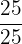 
, a terceira por 
e a quarta por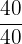 
, obtendo:
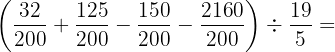
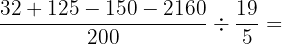
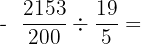
Efetuamos as operações e simplificamos o resultado:
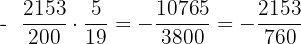
2. Uma caixa contém 
bombons. Eva comeu 
dos bombons e Ana 
.
a Quantos bombons Eva e Ana comeram?
Eva comeu 
bombons e Ana 
.
b Que fração dos bombons elas comeram juntas?
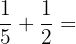
O MMC é 
.
Multiplicamos a primeira fração por 
e a segunda por 
, obtendo:
3. Um pai divide R$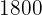 
entre seus filhos. Ao mais velho, dá 
dessa quantia, ao do meio 
e ao mais novo, o restante. Quanto recebeu cada um? Que fração do total recebeu o terceiro?
Mais velho:
O mais velho recebeu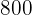 
reais.
Do meio:
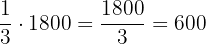
O do meio recebeu 
reais.
Mais novo: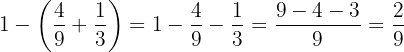
Recebeu 
dos 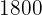reais.
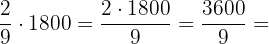
O mais novo recebeu 
reais.
4. Uma família consumiu, em um dia de verão:
Duas garrafas de um litro e meio de água.
garrafas de de litro de suco.
limonadas de 
de litro.
Quantos litros de líquido foram consumidos? Expresse o resultado como número misto.
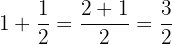
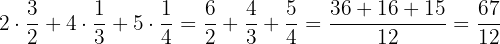
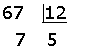
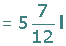
Resumir com IA:
Gostou desse artigo? Deixe uma nota!
Loading...
