Temas
Um radical é uma expressão de  , em que
, em que  e
e  . Além disso, se
. Além disso, se  é par, então
é par, então  não pode ser negativo
não pode ser negativo  .
.
Por exemplo, sabemos que  é par. Portanto,
é par. Portanto, 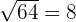 ; enquanto que
; enquanto que  .
.
Do mesmo modo, como  é ímpar, então
é ímpar, então  e
e 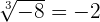 . Isto é, a raiz cúbica está definida para qualquer número real.
. Isto é, a raiz cúbica está definida para qualquer número real.
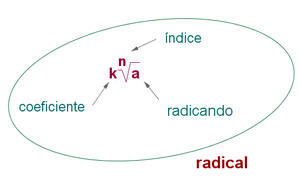
As partes que compõem um radical são: coeficiente, índice e radicando

Potências e radicais
Podemos expressar um radical em forma de potência:
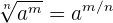
Exemplo: Escreva em forma de potência 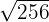
Passe o radicando para potência

Transformamos o índice do radical  em denominador e o expoente do radicando
em denominador e o expoente do radicando 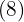 em numerador. Em seguida efetuamos as operações:
em numerador. Em seguida efetuamos as operações:
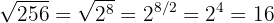
Radicais equivalentes
Utilizando a notação de expoente fracionário e a propriedade das frações, que nos diz que se multiplicamos numerador e denominador por um mesmo número a fração será equivalente, então:
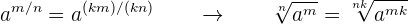
Se multiplicamos ou dividimos o índice e o expoente ou os expoentes do radicando por um mesmo número natural, obteremos outro radical equivalente.
Exemplo: Um radical equivalente de  é
é 
Multiplicamos o índice e o expoente do radicando por um inteiro positivo, por exemplo 
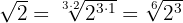
Simplificação de radicais
Se existe um número natural que possa ser dividido pelo índice e o expoente (ou os expoentes) do radicando, obteremos um radical simplificado.
Exemplo: Simplifique,
1 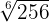
2 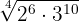
1 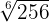 Passe para potência
Passe para potência 

Para simplificar o radical dividimos por  tanto o índice
tanto o índice  como o expoente do radicando
como o expoente do radicando 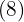
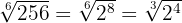
2 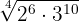
Para simplificar o radical dividimos por  tanto o índice
tanto o índice  como os expoentes do radicando
como os expoentes do radicando 
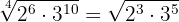
Redução ao índice comum
Para reduzir ao índice comum dois ou mais radicais:
- Encontramos o mínimo múltiplo comum dos índices, que será o índice comum
- Dividimos o índice comum por cada um dos índices e cada resultado obtido vamos multiplicar pelos seus expoentes correspondentes
Exemplo: Passe para índice comum os radicais: 
Em primeiro lugar, encontramos o MMC dos índices: 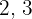 e
e 
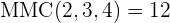
Dividimos o índice comum  por cada um dos índices
por cada um dos índices 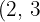 e
e 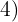 e cada resultado obtido vamos multiplicar pelos seus expoentes correspondentes
e cada resultado obtido vamos multiplicar pelos seus expoentes correspondentes

Operamos com as potências

Extração de fatores em um radical
Para extrair fatores de um radical decompomos o radicando em fatores. Se:
Um expoente do radicando é menor que o índice
Deixamos o fator correspondente no radicando.
Exemplo: Verifique se é possível extrair os fatores de:
1
2 
1 já que
já que 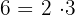 e os expoentes dos fatores é 1, do qual é menor que o índice 2; então
e os expoentes dos fatores é 1, do qual é menor que o índice 2; então
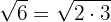
2 
Já que 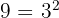 e o expoente 2 é menor que o índice 3; então
e o expoente 2 é menor que o índice 3; então

Um expoente do radicando é igual ao índice
O fator correspondente sai do radicando.
Exemplo: Extraia os fatores de:
1 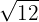
2 
1 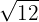 Decompomos
Decompomos  em fatores, como o
em fatores, como o  está elevado a mesma potência que o índice, podemos extrair o
está elevado a mesma potência que o índice, podemos extrair o  do radicando; assim obtemos
do radicando; assim obtemos

2 
Decompomos  em fatores, como o
em fatores, como o  está elevado à mesma potência que o índice, podemos extrair o
está elevado à mesma potência que o índice, podemos extrair o  do radicando; assim obtemos
do radicando; assim obtemos
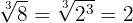
Um expoente do radicando é maior que o índice
Dividimos o expoente pelo índice. O quociente obtido é o expoente do fator fora do radicando e o resto é o expoente do fator dentro do radicando
Exemplo: Extraia os fatores de:
1 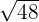
2 
3 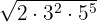
4 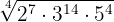
1 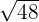 O expoente do 2 é maior que o índice, portanto, dividimos o expoente
O expoente do 2 é maior que o índice, portanto, dividimos o expoente  entre o índice
entre o índice 
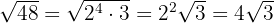
O quociente obtido  é o expoente do fator fora do radicando e o resto
é o expoente do fator fora do radicando e o resto 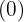 é o expoente do fator dentro do radicando.
é o expoente do fator dentro do radicando.
Como o fator  é igual a 1, não é necessário colocá-lo no radicando já que ele não varia se for multiplicado por outro fator
é igual a 1, não é necessário colocá-lo no radicando já que ele não varia se for multiplicado por outro fator
De maneira geral, se o resultado de dividir o expoente de um fator pelo índice for zero como resto, não colocaremos esse fator no radicando
2 
Decompomos em fatores: 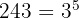
O expoente é maior que o índice, portanto, dividimos o expoente  entre o índice
entre o índice 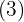 .
.
O quociente obtido  é o expoente do fator fora do radicando e o resto
é o expoente do fator fora do radicando e o resto  é o expoente dentro do radicando
é o expoente dentro do radicando

3 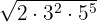
Há expoentes no radicando maiores que o índice, portanto, dividimos os expoentes 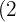 e
e 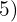 pelo índice
pelo índice  .
.
Cada um dos quocientes  e
e  obtidos será o expoente do fator correspondente fora do radicando e cada um dos restos obtidos
obtidos será o expoente do fator correspondente fora do radicando e cada um dos restos obtidos  e
e  serão os expoentes dos fatores correspondentes dentro do radicando
serão os expoentes dos fatores correspondentes dentro do radicando

4 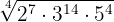
Os expoentes do radicando são maiores que o índice, portanto, dividimos os expoentes  e
e 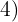 pelo índice
pelo índice  .
.
Cada um dos quocientes 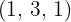 obtidos será o expoente do fator correspondente fora do radicando e cada um dos restos obtidos
obtidos será o expoente do fator correspondente fora do radicando e cada um dos restos obtidos 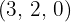 serão os expoentes dos fatores correspondentes dentro do radicando
serão os expoentes dos fatores correspondentes dentro do radicando

Introdução de fatores em um radical
Para introduzir fatores em um radical elevamos os fatores ao índice do radical.
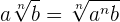
Exemplo: Introduzir os fatores no radical:
1 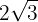
2 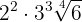
1 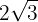 Como o índice é
Como o índice é  , o fator fora do radical
, o fator fora do radical  é elevado ao quadrado, em seguida realizamos as operações
é elevado ao quadrado, em seguida realizamos as operações
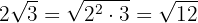
2 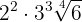
Tanto o  como o
como o  são introduzidos elevados à quarta potência, isto é,
são introduzidos elevados à quarta potência, isto é,
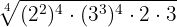
Retiramos os parêntesis multiplicando os expoentes, em seguida multiplicamos as potências com a mesma base

Operações com radicais
Para os radicais temos as operações de soma, subtração, multiplicação, divisão e outras que veremos a seguir:
Soma e subtração de radicais
Somente podemos somar (ou subtrair) dois radicais quando sãoradicais semelhantes, isto é, se são radicais com o mesmo índice e radicando igual.
Para somar radicais com o mesmo índice e radicando iguais, somamos os coeficientes dos radicais.

Exemplo: Faça as somas:
1 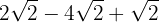
2 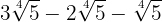
3 
4 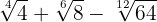
5 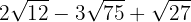
6 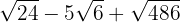
7 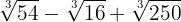
8 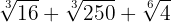
1 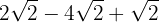 Somamos e subtraímos (dependendo dos sinais) os coeficientes dos radicais, assim
Somamos e subtraímos (dependendo dos sinais) os coeficientes dos radicais, assim
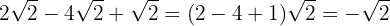
2 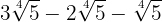
Somamos os coeficientes dos radicais
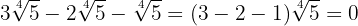
3 
Decompomos os radicandos em fatores:

De modo que as raízes são
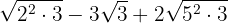
Extraímos os fatores dos radicais e multiplicamos pelo coeficiente do radical correspondente
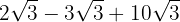
Somamos os coeficientes do radicais
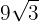
4 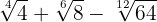
Extraímos fatores dos radicais e multiplicamos pelo coeficiente do radical correspondente
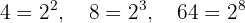
De modo que
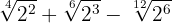
Simplificamos os radicais. No primeiro radical, dividimos o índice e o expoente do radicando por  , no segundo por
, no segundo por  e no terceiro por
e no terceiro por 
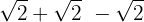
Somamos os coeficientes dos radicais
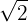
5 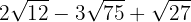
Expressamos os radicandos em fatores
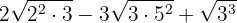
Extraímos os fatores do radicando
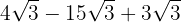
Somamos os coeficientes, assim
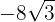
6 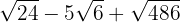
Expressamos os radicandos em fatores
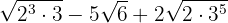
Extraímos os fatores do radicando
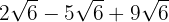
Somamos os coeficientes, assim

7 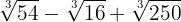
Expressamos os radicandos em fatores
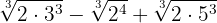
Extraímos os fatores do radicando
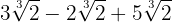
Somamos os coeficientes, assim

8 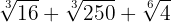
Expressamos os radicandos em fatores
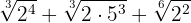
Extraímos os fatores do radicando
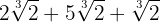
Somamos os coeficientes, assim
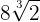
Multiplicação de radicais
Na multiplicação temos dois casos: com o mesmo índice ou com índice diferente
Multiplicação de radicais com o mesmo índice
Para multiplicar radicais com o mesmo índice multiplicamos os radicando deixando-o com o mesmo índice.

Exemplo: Faça a multiplicação 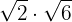
Multiplicamos os radicandos
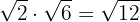
Quando terminamos de fazer uma operação extraímos os fatores do radical, se for possível.
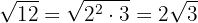
Multiplicação de radicais com índice diferente
Primeiro reduzimos ao mesmo índice comum e em seguida multiplicamos.
Exemplo: Faça as multiplicações:
1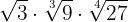
2 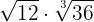
1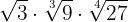 Decompomos os radicandos em fatores
Decompomos os radicandos em fatores

ao mesmo índice comum para isso temos que calcular o mínimo múltiplo comum dos índices, que será o índice comum.
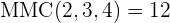
Dividimos o índice comum  por cada um dos índices
por cada um dos índices 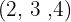 e cada resultado obtido vamos multiplicar pelos seus expoentes correspondentes
e cada resultado obtido vamos multiplicar pelos seus expoentes correspondentes  . Fazemos o produto de potências com a mesma base no radicando e extraímos fatores do radicando
. Fazemos o produto de potências com a mesma base no radicando e extraímos fatores do radicando

2 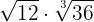
Calculamos o mínimo múltiplo comum dos índices
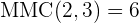
Dividimos o índice comum  por cada um dos índices
por cada um dos índices 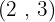 e cada resultado obtido elevamos aos radicandos correspondentes
e cada resultado obtido elevamos aos radicandos correspondentes
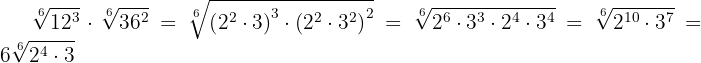
Decompomos em fatores  e
e  , realizamos as operações com as potências e extraímos fatores.
, realizamos as operações com as potências e extraímos fatores.
Divisão de radicais
Na divisão temos dois casos: com o mesmo índice ou com índice diferente
Divisão de radicais com o mesmo índice
Para dividir radicais com o mesmo índice dividimos os radicandos deixando-o com o mesmo índice.
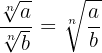
Exemplo: Faça a divisão 
Como os radicais têm o mesmo índice colocamos todos eles com radical com mesmo índice
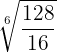
Decompomos em fatores, fazemos a divisão de potências com a mesma base

Simplificamos o radical dividindo o índice e o expoente do radicando por 
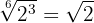
Divisão de radicais com índice diferente
Primeiro reduzimos ao mesmo índice comum e em seguida dividimos.
Exemplo: Faça as divisões:
1 
2 
3 
1  Primeiro reduzimos ao menor índice comum, para isso temos que calcular o mínimo múltiplo comum dos índices, que será o índice comum.
Primeiro reduzimos ao menor índice comum, para isso temos que calcular o mínimo múltiplo comum dos índices, que será o índice comum. 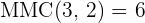 .
.
Dividimos o índice comum  por cada um dos índices (
por cada um dos índices ( e
e  ) e cada resultado obtido vamos multiplicar pelos seus expoentes correspondentes (
) e cada resultado obtido vamos multiplicar pelos seus expoentes correspondentes ( e
e  )
)
2 
Decompomos o  em fatores para poder fazer a divisão de potências com a mesma base e dividimos
em fatores para poder fazer a divisão de potências com a mesma base e dividimos
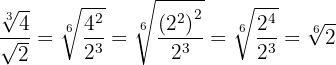
3 
Fazemos os mesmos passos do exemplo anterior

Simplificamos o radical dividindo por  o índice e o expoente do radicando. Por último extraímos fatores
o índice e o expoente do radicando. Por último extraímos fatores
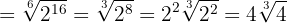
Potência de um radical
Para elevar um radical a uma potência, elevamos à potência o radicando deixando-o com o mesmo índice.
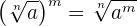
Exemplo: Simplifique,
1 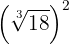
2 
1 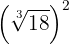 Elevamos o radicando ao quadrado, decompomos
Elevamos o radicando ao quadrado, decompomos  em fatores e elevamos ao quadrado. Por último extraímos fatores
em fatores e elevamos ao quadrado. Por último extraímos fatores
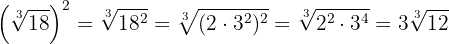
2 
Elevamos os radicandos à quarta, decompomos os radicandos em fatores e extraímos o  do radical
do radical
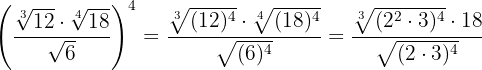
Nos radicando realizamos as operações com potências e passamos para índice comum para poder efetuar a divisão
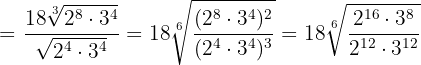
Simplificamos o radical dividindo por  e o índice e os expoentes do radicando, em seguida fazemos uma divisão de potências com o mesmo expoente
e o índice e os expoentes do radicando, em seguida fazemos uma divisão de potências com o mesmo expoente
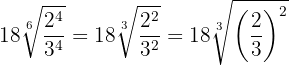
Raiz de um radical
A raiz de um radical é outro radical com um radicando igual e cujo índice é o produto dos dois índices.
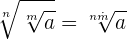
Exemplo: Simplifique,
1 
2 
1  Multiplicamos os índices
Multiplicamos os índices
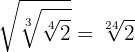
2 
Introduzimos o primeiro  dentro da raiz cúbica, para isso temos que elevá-lo ao cubo. Em seguida multiplicamos as potências com a mesma base
dentro da raiz cúbica, para isso temos que elevá-lo ao cubo. Em seguida multiplicamos as potências com a mesma base
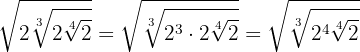
Introduzimos o  na raiz quarta, para isso temos que elevá-lo à quarta. Em seguida realizamos o produto de potências e por último o produtos dos índices
na raiz quarta, para isso temos que elevá-lo à quarta. Em seguida realizamos o produto de potências e por último o produtos dos índices

Racionalização
A racionalização de radicais consiste em retirar os radicais do denominador, o que facilita o cálculo de operações como a soma de frações
Podemos distinguir três casos:
Caso 1
Racionalização do tipo 
Multiplicamos o numerador e denominador por 

Exemplo: Racionalize 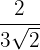
Multiplicamos o numerador e denominador por 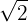
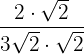
Simplificamos
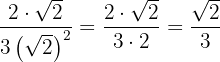
Caso 2
Racionalização do tipo 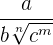
Multiplicamos o numerador e denominador por 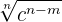

Exemplo: Racionalize 
Colocamos o radicando  em forma de potência:
em forma de potência: 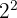
Temos que multiplicar o numerador e denominador pela raiz quinta de 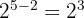
Multiplicamos os radicais do denominador, extraímos fatores do radical e simplificamos a fração

Caso 3
Racionalização do tipo 
De maneira geral quando o denominador é um binômio com ao menos um radical.
Multiplicamos o numerador e denominador pelo conjugado do denominador.
O conjugado de um binômio é igual ao binômio com o sinal central trocado:
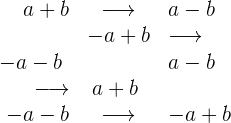
Também temos que levar em conta que: "a soma pela diferença é igual a diferença dos quadrados".

Exemplo: Racionalize,
1 
2 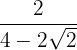
3 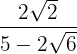
1  Multiplicamos o numerador e denominador pelo conjugado do denominador, retiramos os parêntesis do numerador e efetuamos a soma pela diferença no denominador, assim obtemos uma diferença de quadrados
Multiplicamos o numerador e denominador pelo conjugado do denominador, retiramos os parêntesis do numerador e efetuamos a soma pela diferença no denominador, assim obtemos uma diferença de quadrados
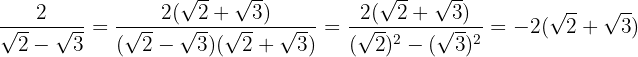
2 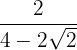
Multiplicamos e dividimos a fração pelo conjugado do denominador
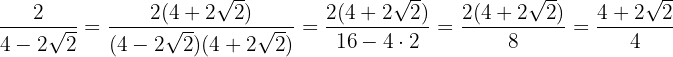
3 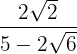
Multiplicamos o numerador e denominador pelo conjugado do denominador, retirarmos os parêntesis do numerador e efetuamos a soma pela diferença no denominador, assim obtemos uma diferença de quadrados
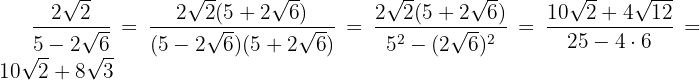
Resumir com IA:












