Definição de matriz inversa
Dizemos que uma matriz quadrada 
possui inversa quando existe uma matriz 
tal que:
onde 
é a matriz identidade. A matriz é única e é chamada de inversa de , sendo representada por: 
Ou seja,
.
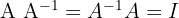Observação importante: Uma matriz quadrada só possui inversa quando seu determinante é diferente de zero.
Ou seja, uma matriz tem inversa se, e somente se, seu determinante é não nulo.
Propriedades da matriz inversa
A inversa de uma matriz possui as seguintes propriedades:
1 Se e são matrizes quadradas da mesma ordem que possuem inversa, então o produto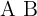 
também possui inversa, e: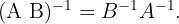 
2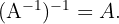 
3 Seja 
um número real diferente de zero, então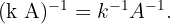 
4 Se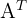 
representa a transposta de uma matriz, então: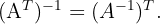 
- A matriz inversa é uma ferramenta importante na resolução de sistemas de equações lineares, pois qualquer sistema pode ser escrito na forma:
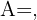onde é a matriz dos coeficientes do sistema, 
é o vetor coluna que contém as variáveis desconhecidas, e 
é o vetor coluna cujos elementos são os termos constantes do lado direito das equações do sistema.
Por exemplo, o sistema:
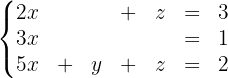
pode ser expressado como a equação matricial 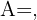onde:
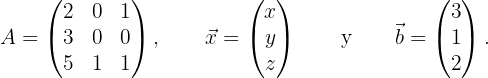
Considerando que a matriz dos coeficientes é quadrada, ela pode possuir inversa. Se possui inversa e temos uma forma de calcular essa inversa 
, então podemos determinar simplesmente por meio de uma multiplicação de matrizes: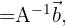
, isso porque,
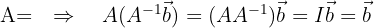
Ou seja, resolvemos o sistema de equações.
Assim, uma das aplicações mais úteis da inversa de uma matriz é a resolução eficiente de sistemas de equações lineares.
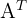Lembrando que a matriz transposta de uma matriz é representada por ye se obtém trocando suas linhas por colunas (ou colunas por linhas).Por exemplo, continuando com a matriz acima, temos que, se:
Pode-se calcular a inversa de uma matriz por dois métodos: pelo método de Gauss e pelo método da adjunta. Neste último, é onde aparece a matriz transposta. Assim, uma das aplicações práticas mais importantes da matriz transposta é no cálculo da matriz inversa.
Já estudamos o método de Gauss em outro artigo. Agora, vamos concentrar nossa atenção no método da adjunta.
Cálculo pelo método da adjunta
O cálculo da inversa de uma matriz pelo método da adjunta baseia-se no seguinte resultado:
onde,
Para entender a operação, vamos analisar um exemplo:
Exemplo: Cálculo da matriz inversa
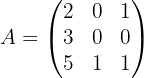
que corresponde aos coeficientes do sistema de equações lineares acima.
Solução:
Para calcular a inversa, seguimos os seguintes passos:
1 Calculamos o determinante da matriz:
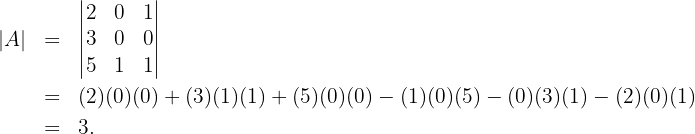
Como o determinante é diferente de zero, a matriz possui inversa.
2 A matriz adjunta é aquela em que cada elemento da matriz original é substituído por seu cofator.
Ou seja,
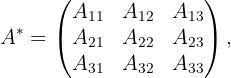
onde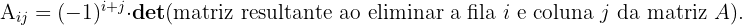 
Dessa forma,
Portanto,
3 Calculamos a transposta da matriz adjunta:
Se:
4 A matriz inversa é igual à transposta da matriz adjunta dividida pelo determinante da matriz original.
Ou seja:
Portanto,
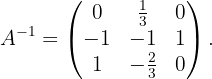
Assim, obtemos a inversa da matriz .
Observação: Como comentário final, podemos resolver o sistema de equações lineares apresentado anteriormente utilizando:
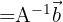obtendo que,
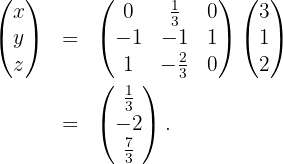
Portanto, a escolha de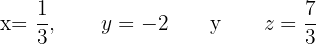 
resolve o sistema apresentado anteriormente, como pode ser facilmente verificado.
Gostou desse artigo? Deixe uma nota!
Loading...
