Temas
O que é um histograma?
Um histograma é a representação gráfica em forma de barras que mostra a distribuição de um conjunto de dados. Ele serve para obter uma “primeira visão geral”, ou panorama, da distribuição de uma população ou de uma amostra em relação a uma característica quantitativa contínua.
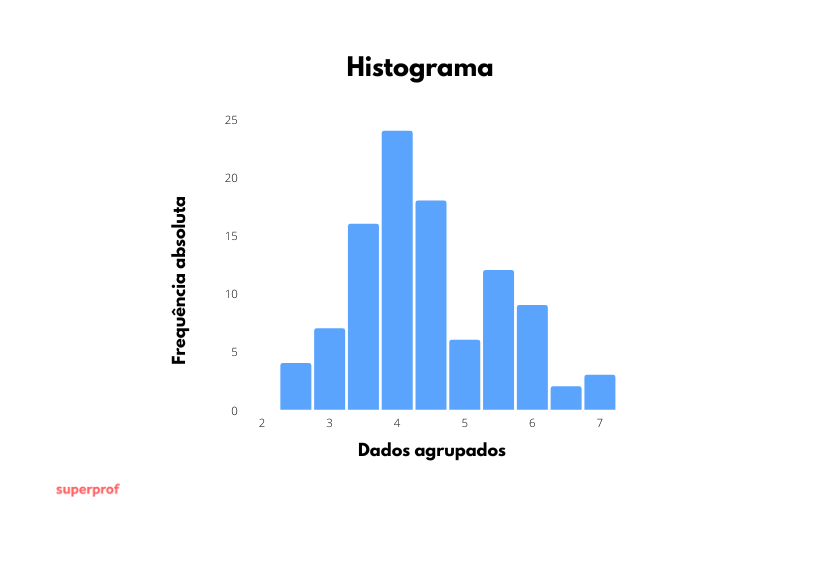
Em um histograma, o eixo das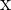 
((ou abscissas) corresponde ao intervalo de valores no qual se encontram os dados. As bases dos retângulos representam os intervalos de classe nos quais agrupamos essas informações.
Por outro lado, no eixo das 
podemos ter diferentes opções — e é isso que define o tipo de histograma.
Os dois principais tipos são:
- Histograma de frequências absolutas. Representa a frequência absoluta por meio da altura das barras.
- Histograma de frequências relativas. Representa a frequência relativa por meio da altura das barras.
Assim, conhecendo as características de um histograma, para construí-lo a partir de um conjunto de dados, devemos seguir os seguintes passos:
- Desenhar o eixo das abscissas, incluindo no mínimo o intervalo total dos dados, e dividi-lo em intervalos (ou classes).
- Desenhar o eixo das ordenadas, representando as frequências absolutas ou relativas, conforme o caso.
- Traçar os retângulos de mesma largura (proporcional à amplitude do intervalo) e altura igual à frequência correspondente.
Exemplo: Vamos considerar os seguintes dados:
| Idade | Pessoas |
|---|---|
 |  |
 |  |
 |  |
 |  |
 | |
 |  |
 |  |
 |  |
 |  |
 |  |
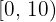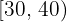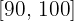| Total: |  |
O histograma de frequências absolutas seria o seguinte.
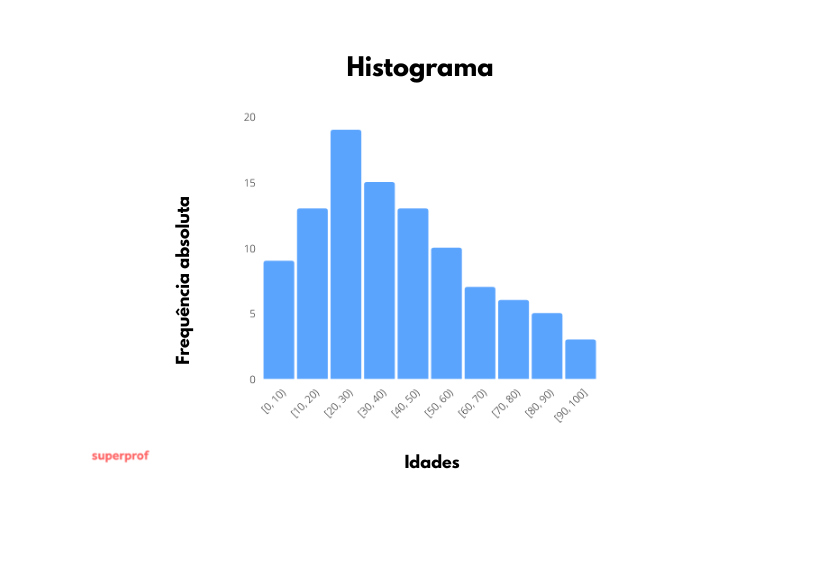
Por outro lado, o histograma de frequências relativas seria assim:
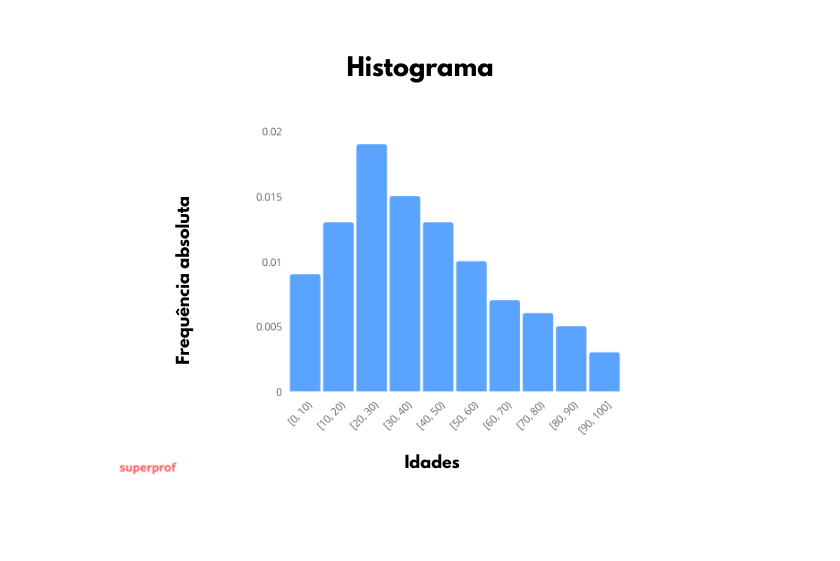
Polígono de frequências
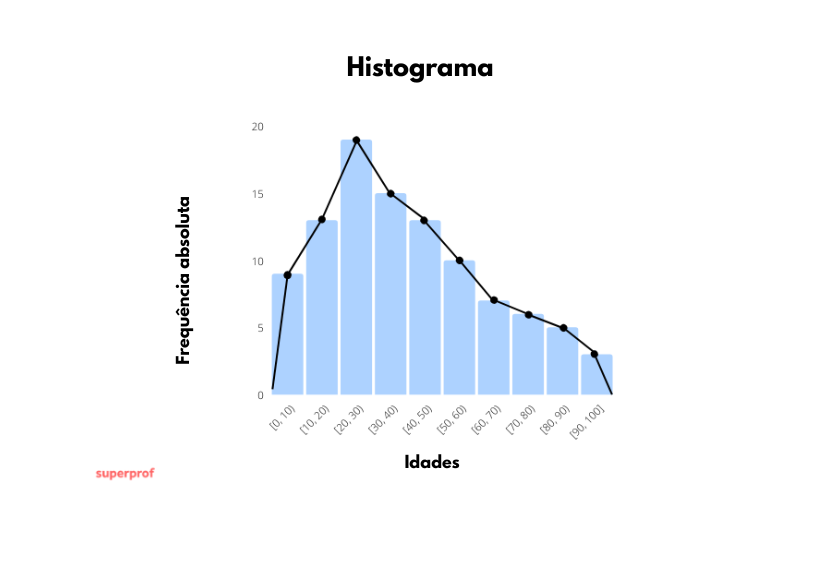
Um polígono de frequências mostra a mesma informação do histograma. Para construí-lo, marcamos um ponto para cada classe: no eixo das abscissas, usamos o ponto médio da classe e no eixo das ordenadas, a altura correspondente à frequência da classe (igual à altura do retângulo do histograma).
Por fim, unimos cada ponto ao seu sucessor e ao seu antecessor.
Exemplo: Usando o mesmo conjunto de dados do exemplo anterior:
| Idade | Pessoas | Frequência Acumulada |  |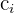
|---|---|---|---|
| | | |
| |  | |
| |  |  |
| |  |  |
| |  |  |
| |  |  |
| |  |  |
| |  |  |
| |  |  |
| | |  |
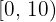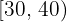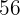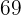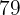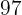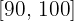| Total: | |
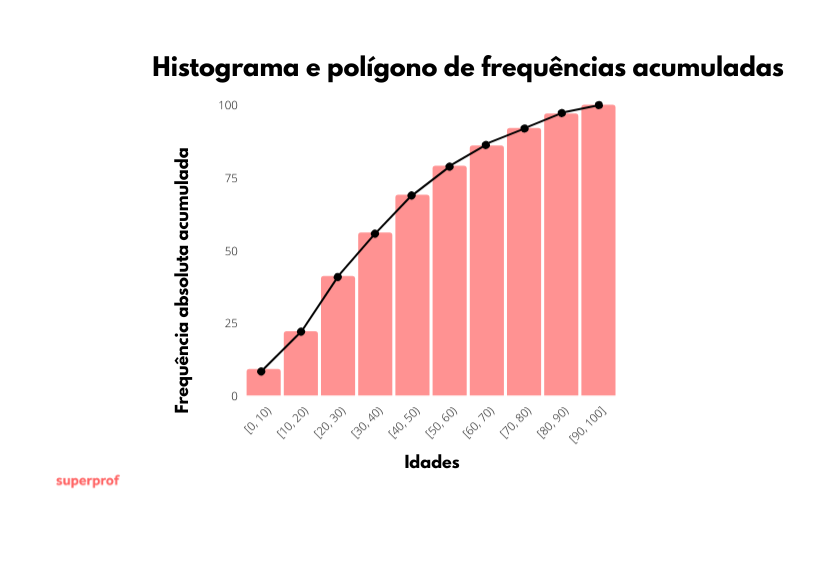
Histograma e polígono de frequências acumuladas
Quando representamos as frequências acumuladas de uma tabela de dados agrupados, obtemos o histograma de frequências acumuladas e o polígono acumulado correspondente.
Exemplo: Usando o mesmo conjunto de dados do exemplo anterior:
| Idade | Pessoas | Frequência Acumulada | |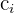
|---|---|---|---|
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
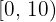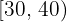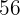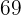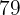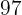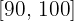| Total: | |
Histogramas com intervalos de amplitudes diferentes
Nesse caso, o histograma deve representar a frequência de cada intervalo pela área da barra, e não apenas por sua altura.
Assim, a altura de cada barra é calculada da seguinte forma:
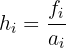
Onde:
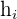é a altura do intervalo,- é a frequência absoluta ou relativa do intervalo, conforme o caso,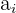
é a amplitude da classe.
A ideia do polígono de frequências continua exatamente a mesma.
Exemplo: Conside uma nova forma de agrupar os dados do exemplo anterior:
| Idade | 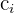| Pessoas | Frequência 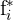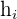relativa  | relativa |
|---|---|---|---|---|
| | |  |  |
| | |  |  |
| | |  |  |
 | |  |  |  |
| | |  |  |
| | |  |  |
| | |  |  |
| | |  |  |
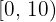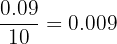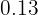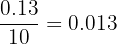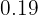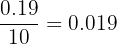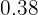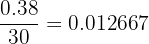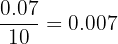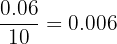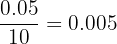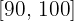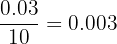| Total: | |  |
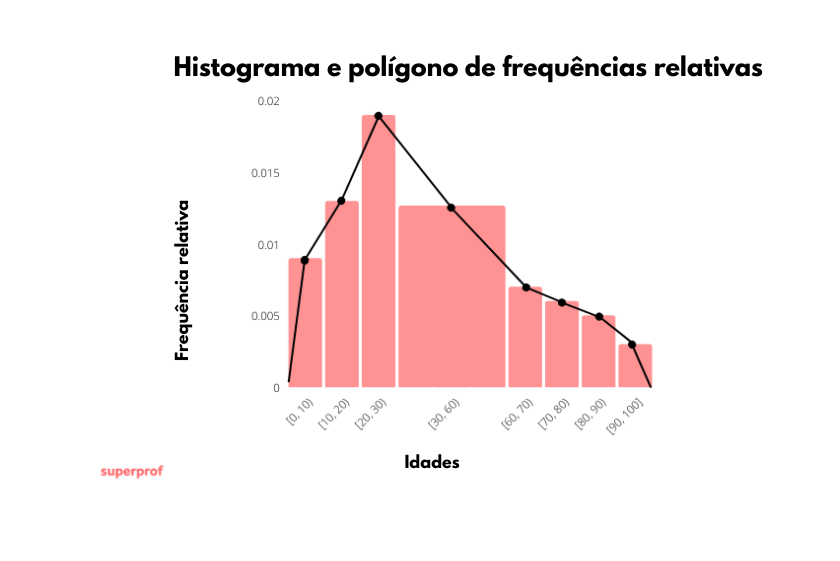
O histograma e o polígono de frequências relativas seria representado assim:
Gostou desse artigo? Deixe uma nota!
Loading...
