Temas

Definição de moda estatística
- A moda é o valor que tem maior frequência absoluta.
- É representada por
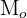
- Se em um grupo há duas ou várias pontuações com a mesma frequência e essa frequência é a máxima, então a distribuição é bimodal (no caso de que sejam
 valores) ou multimodal (no caso de que existam mais de
valores) ou multimodal (no caso de que existam mais de  ), isto é, tem várias modas.
), isto é, tem várias modas. - Quando todas as pontuações de um grupo tem a mesma frequência, não há moda.
- Podemos encontrar a moda para variáveis qualitativas e quantitativas.
- Quando todas as pontuações de um grupo tem a mesma frequência, não há moda.
- Se duas pontuações adjacentes têm a frequência máxima, a moda é o promédio das duas pontuações adjacentes.
Exemplos de cálculo da moda
1 Encontre a moda da distribuição: 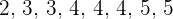
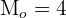
2 Encontre a moda da distribuição: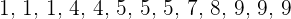
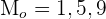
3 Encontre a moda da distribuição: 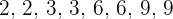
Como todas as pontuações do grupo têm a mesma frequência, não há moda.
4 Encontre a moda da distribuição: 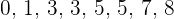
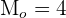
Cálculo da moda para dados agrupados
Caso 1: Quando todos os intervalos têm a mesma amplitude.
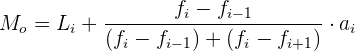
 é o limite inferior da classe modal
é o limite inferior da classe modal é a frequência absoluta da classe modal
é a frequência absoluta da classe modal é a frequência absoluta imediatamente inferior à classe modal
é a frequência absoluta imediatamente inferior à classe modal é a frequência absoluta imediatamente posterior à classe modal
é a frequência absoluta imediatamente posterior à classe modal é a amplitude da classe
é a amplitude da classe
Também podemos utilizar outra fórmula da moda que dá um valor aproximado dela:
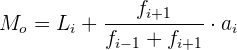
Exemplo:
Calcule a moda de uma distribuição estatística que vem dada na seguinte tabela:
 | |
|---|---|
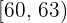 |  |
 |  |
 |  |
 |  |
 |  |
 |
Em primeiro lugar, procuramos o intervalo onde a moda se encontra, que será o intervalo que tenha a maior frequência absoluta  .
.
A classe modal é: 
Aplicamos a fórmula para o cálculo da moda para dados agrupados extraindo os seguintes dados:
Limite inferior: 
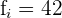

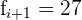

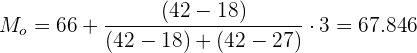
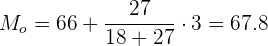
Caso 2: Quando os intervalos têm amplitudes diferentes.
1 Em primeiro lugar, temos que encontrar as alturas.

2 A classe modal é a que tem maior altura.
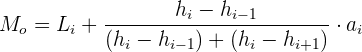
3 A fórmula da moda aproximada quando existem diferentes amplitudes é:
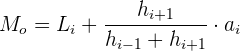
Exemplo:
Na seguinte tabela são mostradas as qualificações de (reprovado, aprovado, notável e excelente) obtidas por um grupo de 50 alunos. Calcule a moda.
 | |
|---|---|
 |  |
 |  |
 |  |
 |  |
Em primeiro lugar, vamos criar uma nova coluna com as alturas, dividindo as frequências absolutas entre as amplitudes dos intervalos correspondentes:


 | 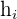 | |
|---|---|---|
 |  |  |
 |  |  |
 |  |  |
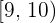 |  |  |
 |
A classe modal é  porque é a que têm maior altura
porque é a que têm maior altura
Limite inferior: 
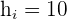
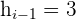
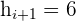
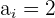
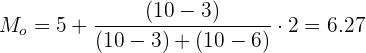
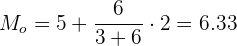
Resumir com IA:












