Temas
Definição
A média aritmética é o valor obtido ao somar todos os dados e dividir o resultado entre o número total de dados. Indicamos a média com o símbolo de 
e calculamos ela da seguinte maneira
onde cada 
representa um dos nossos dados e 
é o número total de dados que temos.
Exemplo:
Os pesos de seis amigos são: 
e 
.
Encontre o peso médio.
Primeiro, note que temos seis dados, portanto, 
. Procedemos à calcular a média
Média aritmética para dados agrupados
Quando os dados vêm agrupados em uma tabela de frequências, a expressão da média é distinta. Supomos que temos 
classes diferentes em nossa tabela de frequências, onde para cada classe 
, temos sua média e sua frequência 
correspondente, então calculamos a média como:
Devemos observar que agora é a soma das frequências de cada classe, isto é
.
Além disso, quando cada grupo ou classe é um intervalo, a média desse intervalo é simplesmente o ponto médio entre os limites. Assim, supondo que um grupo é o intervalo 
, então sua média é 
.
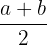Como aviso, note que por havermos uma tabela de frequência e por haver agrupado os dados, nós substituímos cada dado pela média do grupo ou classe ao qual pertencem, e que a soma de todas as frequências é igual à quantidade de dados que teríamos se não tivéssemos agrupado. Portanto, ao calcular a média em dados agrupados, o que fazemos é simplesmente substituir cada dado pela média do grupo ou classe ao qual pertencem. No caso de haver dados agrupados, de maneira geral, é melhor não agrupar, já que isto implica uma perda de informação.
Exercícios de média aritmética para dados agrupados
Em um teste realizado em um grupo de 42 pessoas foram obtidos os seguintes pontos mostrados na tabela.
Calcule a pontuação média.
| | |
|---|---|---|
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  | |
 |  |  |
 |  |  |
Podemos observar como cada é o ponto médio do intervalo correspondente.
Para obter a média, em primeiro lugar, vamos calcular a somatória de 
, criaremos uma nova coluna para os produtos da variável com sua frequência absoluta correspondente e depois vamos somar tudo. Também temos que calcular que é a somatória das frequências absolutas.
| | | |
|---|---|---|---|
| | | |
| | |  |
| | |  |
| | |  |
| | |  |
| | |  |
| | |  |
| Somas: |  |  |
Então, utilizando nossos dados, a média está dada por:
Propriedades da média aritmética
Primeiro, uma definição que nos ajudará a entender melhor as definições. Sendo 
um conjunto de dados e a média de dados, então, definimos a desviação de um dado em relação à média como:
.
1. A soma das desviações de todos os dados de uma distribuição em relação à média dela igual a zero. Isto é
A soma das desviações dos números 
da sua média aritmética 
é igual a 
:
2. A soma dos quadrados das desviações e dos valores da variável em relação a um número qualquer é mínima quando este número coincide com a média aritmética. Em outras palavras, sempre se cumpre o seguinte:
3. Se somamos um mesmo número a todos os valores de uma variável, a média aritmética destes novos dados é a média dos anteriores mais a mesma quantidade em que somamos aos dados. Isto é, supondo que temos os dados 
com média , agora, se somarmos em todos os dados uma quantidade 
, 
, a média destes novos dados é:
4. Se todos os valores de uma variável são multiplicados por um mesmo número, a média aritmética fica multiplicada por este número. Isto é, supondo que temos os dados com média , agora, se multiplicarmos todos os dados por uma quantidade , 
, a média destes novos dados é:
Observações sobre a média aritmética
1. A média pode ser encontrada apenas para as variáveis quantitativas.
2. A média é independente das amplitudes dos intervalos.
3. A média é muito sensível às pontuações extremas, também conhecidas como valores atípicos. Se temos uma distribuição com os seguintes pesos:
.
A média é igual a 
, que é uma medida de centralização pouco representativa da distribuição. No entanto, isto ocorre porque temos um dado muito distanciado dos demais, 
.
4. A média não pode ser calculada se há um intervalo com uma amplitude indeterminada.
| | |
|---|---|---|
 |  |  |
 |  |  |
 |  | |
 |  |  |
 | | |
 |
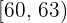Neste caso, não é possível encontrar a média porque não podemos calcular a marca de classe do último intervalo.
Gostou desse artigo? Deixe uma nota!
Loading...
