
Máximo Divisor Comum
O máximo divisor comum, 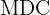 de dois ou mais números o maior divisor entre dois ou mais números inteiros, de maneira exata.
de dois ou mais números o maior divisor entre dois ou mais números inteiros, de maneira exata.
Cálculo do máximo divisor comum
1Decomponha todos números em fatores primos.
2Identifique os fatores primos comuns com o menor expoente.
3Multiplique esses fatores para encontrar o resultado.
Exemplo: Encontre o 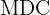 de:
de: 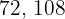 e
e 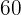 .
.
1 Vamos decompor os números em fatores primos

Assim, os números são escritos dessa forma:

2Os fatores comuns de menor expoente são 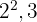
3Para calcular o 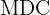 multiplicamos os fatores comuns com o menor expoente:
multiplicamos os fatores comuns com o menor expoente:
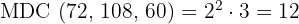
É importante observar que, se um número é divisor de outro, então esse número é o 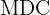 de ambos
de ambos
Exemplo: O número  é divisor de
é divisor de  , portanto
, portanto 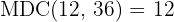
Mínimo Múltiplo Comum
O mínimo múltiplo comum 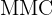 é o menor dos múltiplos comuns a vários números, excluindo o zero.
é o menor dos múltiplos comuns a vários números, excluindo o zero.
Cálculo do mínimo múltiplo comum
1Decomponha os números em fatores primos.
2Identifique os fatores primos comuns e não comuns com o maior expoente.
3Multiplique esses fatores para encontrar o resultado.
Exemplo: Encontre o 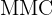 de:
de: 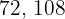 e
e 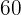 .
.
1Vamos decompor os números em fatores primos:

Dessa forma, vamos escrever os números assim:

2Os fatores comuns e não comuns com o maior expoente são 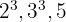
3Para calcular o 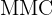 multiplicamos os fatores primos comuns e não comuns com o maior expoente.
multiplicamos os fatores primos comuns e não comuns com o maior expoente.
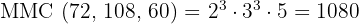
Dessa forma,  é o menor número que pode ser dividido por
é o menor número que pode ser dividido por 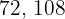 e
e 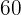 .
.
É importante perceber que, se um número é múltiplo de outro, então este será o 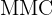 dos dois.
dos dois.
Exemplo: O número  é múltiplo de
é múltiplo de  , de forma que o
, de forma que o 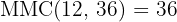
Relação entre o Máximo Divisor Comum e o Mínimo Múltiplo Comum
Considerando que o máximo divisor comum (MDC) e o mínimo múltiplo comum (MMC) são formados pelo produto dos fatores comuns com o menor expoente e pelo produto dos fatores comuns e não comuns com o maior expoente, respectivamente, então:
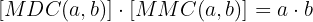
Exercícios propostos
Calcule o 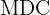 e o
e o 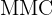 de
de  e
e 
a. Vamos decompor os números em fatores primos

Assim, os números podem ser escritos da seguinte forma:

b. Os fatores comuns com menor expoente são 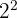
c. Para calcular o 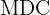 , multiplicamos os fatores comuns com o menor expoente:
, multiplicamos os fatores comuns com o menor expoente:
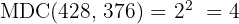
d. Os fatores comuns e não comuns com o maior expoente são 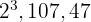
e. Para calcular o 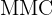 , multiplicamos os fatores comuns e não comuns com o maior expoente:
, multiplicamos os fatores comuns e não comuns com o maior expoente:
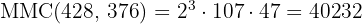
Calcule o 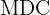 e
e 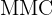 de
de  e
e 
a. Decompondo os números em fatores primos:
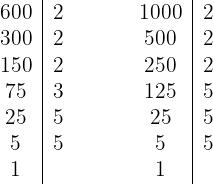
Assim, os números podem ser escritos da seguinte forma:
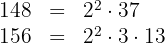
b. Os fatores comuns com o menor expoente são:
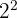
c. Para calcular o 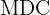 , multiplicamos os fatores comuns com o menor expoente:
, multiplicamos os fatores comuns com o menor expoente:
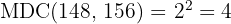
d. Os fatores comuns e não comuns com o maior expoente são:
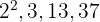
e. Para calcular o 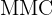 , multiplicamos os fatores comuns e não comuns com o maior expoente:
, multiplicamos os fatores comuns e não comuns com o maior expoente:
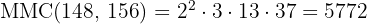
Calcule o 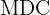 e o
e o 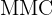 de
de  e
e 
a. Decompondo os números em fatores primos:

Assim, os números podem ser escritos como:
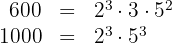
b. Os fatores comuns com menor expoente são:
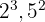 .
.
c. Para calcular o 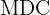 , multiplicamos os fatores comuns com menor expoente:
, multiplicamos os fatores comuns com menor expoente:
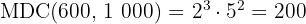
c. Os fatores comuns e não comuns com maior expoente são:
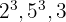 .
.
d. Para calcular o 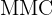 , multiplicamos os fatores comuns e não comuns com maior expoente:
, multiplicamos os fatores comuns e não comuns com maior expoente:
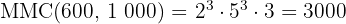
Calcule o 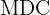 e o
e o 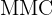 de
de  e
e 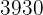
a. Decompondo os números em fatores primos:
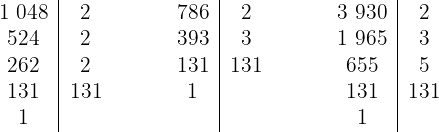
Assim, os números podem ser escritos como:
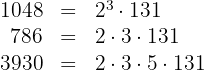
b. Os fatores comuns com menor expoente são:
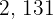 .
.
c. Para calcular o 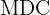 , multiplicamos os fatores comuns com menor expoente:
, multiplicamos os fatores comuns com menor expoente:
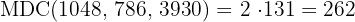
d. Os fatores comuns e não comuns com maior expoente são:  .
.
e. Para calcular o 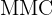 , multiplicamos os fatores comuns e não comuns com maior expoente:
, multiplicamos os fatores comuns e não comuns com maior expoente:
Calcule o 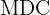 e o
e o 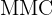 de
de 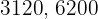 e
e 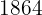
a. Decompondo os números em fatores primos:
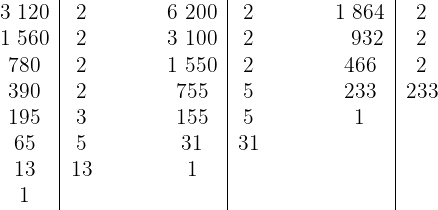
Assim, os números podem ser escritos como:
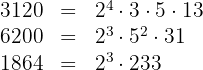
b. O fator comum com menor expoente é: 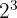 .
.
c. Para calcular o 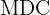 , multiplicamos os fatores comuns com menor expoente:
, multiplicamos os fatores comuns com menor expoente:
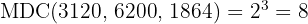
d. Os fatores comuns e não comuns com maior expoente são:
 .
.
e. Para calcular o 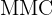 , multiplicamos os fatores comuns e não comuns com maior expoente:
, multiplicamos os fatores comuns e não comuns com maior expoente:
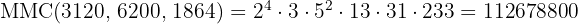
Um farol acende a cada  segundos, outro a cada
segundos, outro a cada  segundos e um terceiro a cada minuto. Às
segundos e um terceiro a cada minuto. Às 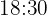 , os três coincidem. A que horas voltarão a coincidir novamente?
, os três coincidem. A que horas voltarão a coincidir novamente?
Vamos começar decompondo os números em fatores primos:
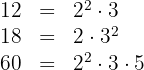
Agora, vamos calcular o 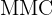 dos três números:
dos três números:
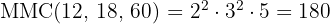
Os faróis coincidem a cada 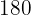 segundos - o que equivale a
segundos - o que equivale a  minutos. Portanto, voltarão a coincidir às
minutos. Portanto, voltarão a coincidir às 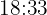 .
.
Um vendedor vai a Brasília a cada  dias para treinamento e outro a cada
dias para treinamento e outro a cada  dias. Hoje, os dois estiveram na Capital Federal. Em quantos dias voltarão a se encontrar em Brasília?
dias. Hoje, os dois estiveram na Capital Federal. Em quantos dias voltarão a se encontrar em Brasília?
Primeiro, vamos decompor os números em fatores primos:
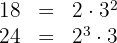
Então, calculamos o 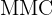 dos dois números:
dos dois números:
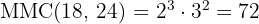
Desta forma, os dois vendedores voltarão a se encontrar em  dias.
dias.
Qual é o menor número que, ao ser dividido por  e
e 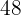 , deixa resto
, deixa resto  em todas as divisões?
em todas as divisões?
Decompondo os números em fatores primos:
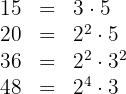
Calculamos o 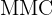 dos quatro números:
dos quatro números:
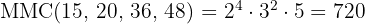
Como 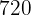 é o menor número divisível pelos quatro valores, para que o resto da divisão seja
é o menor número divisível pelos quatro valores, para que o resto da divisão seja  , o número procurado deve ser:
, o número procurado deve ser:
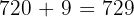 .
.
Em uma adega há  tonéis de vinho com capacidades de
tonéis de vinho com capacidades de 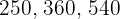 litros, respectivamente. O conteúdo deve ser armazenado em um certo número de garrafas de mesma capacidade. Determine a maior capacidade possível dessas garrafas para que o vinho possa ser armazenado igualmente e o número de garrafas necessárias.
litros, respectivamente. O conteúdo deve ser armazenado em um certo número de garrafas de mesma capacidade. Determine a maior capacidade possível dessas garrafas para que o vinho possa ser armazenado igualmente e o número de garrafas necessárias.
Decompondo os números em fatores primos:
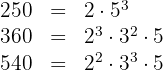
Calculamos o 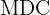 dos três números:
dos três números:
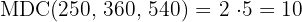
A capacidade de cada garrafa será de  litros, e o número total de garrafas será:
litros, e o número total de garrafas será:
 garrafas.
garrafas.
O piso de uma sala, que será trocado, tem 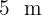 de comprimento e
de comprimento e 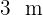 de largura. Determine o lado, em decímetros, dos maiores porcelanatos quadrados possíveis que podem ser usados sem cortes e o número total necessário.
de largura. Determine o lado, em decímetros, dos maiores porcelanatos quadrados possíveis que podem ser usados sem cortes e o número total necessário.
a. Convertendo as dimensões para decímetros:
 (comprimento) e
(comprimento) e 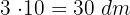 (largura).
(largura).
b. Calculamos o 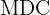 dos dois números:
dos dois números:
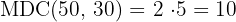
O lado de cada porcelanato será de 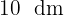 , e serão necessários
, e serão necessários  porcelanatos no comprimento e
porcelanatos no comprimento e  na largura, totalizando:
na largura, totalizando:
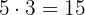 porcelanatos.
porcelanatos.
Um comerciante deseja embalar 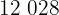 maçãs e
maçãs e 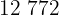 laranjas em caixas, garantindo que cada caixa contenha a mesma quantidade de uma única fruta e que essa quantidade seja a maior possível. Determine o número de laranjas por caixa e o número total de caixas necessárias.
laranjas em caixas, garantindo que cada caixa contenha a mesma quantidade de uma única fruta e que essa quantidade seja a maior possível. Determine o número de laranjas por caixa e o número total de caixas necessárias.
Calculamos o 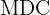 :
:
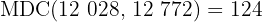
Calculamos o número de caixas necessárias:

Assim, o número total de caixas necessárias será:
 .
.
Qual é o tamanho do maior azulejo quadrado que pode ser usado para cobrir completamente uma sala de 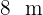 de comprimento por
de comprimento por 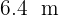 de largura sem precisar cortá-lo? E quantos azulejos serão necessários?
de largura sem precisar cortá-lo? E quantos azulejos serão necessários?
Vamos converter as dimensões para decímetros:
 (comprimento) e
(comprimento) e  (largura).
(largura).
Então, calculamos o 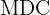 dos dois números:
dos dois números:
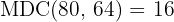
Assim, o tamanho de cada azulejo será de 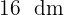 , e serão necessários:
, e serão necessários:
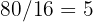 azulejos no comprimento.
azulejos no comprimento.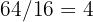 azulejos na largura.
azulejos na largura.
No total, serão usados:
 azulejos.
azulejos.
Resumir com IA:












