
Definição de logaritmo
Expoente do qual temos que elevar a um número, chamado base, para obtermos outro número determinado. Um logaritmo procura o expoente  de uma base
de uma base  que tenham sido usada para chegar a um determinado resultado
que tenham sido usada para chegar a um determinado resultado  .
.
Exemplo:
Se tenho uma base  e
e  como resultado, então a qual expoente devemos elevar o
como resultado, então a qual expoente devemos elevar o  para obtermos
para obtermos  como resultado? Como podemos observar, o valor do expoente que utilizamos para chegar ao resultado
como resultado? Como podemos observar, o valor do expoente que utilizamos para chegar ao resultado  com a base
com a base  é
é  .
.
A notação correspondente para representar um logaritmo é a seguinte:
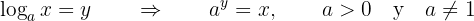
onde  é a base,
é a base,  é o resultado e
é o resultado e  o expoente que procuramos. Lembre-se que devemos cumprir as condições para que a base seja positiva
o expoente que procuramos. Lembre-se que devemos cumprir as condições para que a base seja positiva  e diferente de um.
e diferente de um.
A partir da definição de logaritmo podemos dizer que:
- Não existe logaritmo com base negativa.

- Não existe logaritmo de um número negativo.

- Não existe o logaritmo de zero.
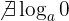
- O logaritmo de 1 é zero.
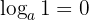
- O logaritmo com base
 a de
a de  a é igual a
a é igual a  .
.
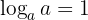
- O logaritmo com base
 a de uma potência com base
a de uma potência com base  a é igual ao expoente.
a é igual ao expoente.
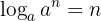
Propriedades dos logaritmos
1 O logaritmo de um produto é igual a soma dos logaritmos dos fatores:
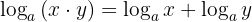
Exemplo:
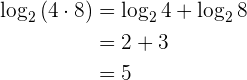
2 O logaritmo de uma quociente é igual ao logaritmo do dividendo menos o logaritmo do divisor:
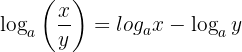
Exemplo:
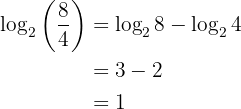
3 O logaritmo de uma potência é igual ao produto do expoente pelo logaritmo da base:
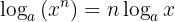
Exemplo:
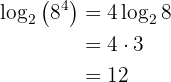
4 O logaritmo de uma raiz é igual ao quociente entre o logaritmo do radicando e o índice da raiz:

Exemplo:
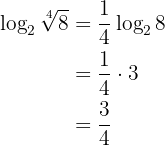
5 Mudança de base:

Exemplo:
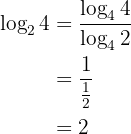
Os logaritmos se tornaram desde sua criação em uma ferramenta importante para o cálculo de operações com números muito grandes, já que têm a propriedade de trabalhar com expoentes e converter os problemas de multiplicação em problemas de soma. Graças às suas propriedades, o logaritmo também permite simplificar diversas operações matemáticas, por isso vale a pena estudá-los.
Resumir com IA:












