Em uma certa rede de centros comerciais trabalham 150 pessoas no departamento pessoal, 450 no departamento de vendas, 200 no departamento de contabilidade e 100 no departamento de atendimento ao cliente. Com o objetivo de fazer uma pesquisa com os funcionários pretende-se selecionar uma amostra com 180 trabalhadores.
Qual tipo de amostragem devemos utilizar para realizar a amostra se queremos que sejam incluídos trabalhadores dos quatro departamentos mencionados?
Qual a quantidade de trabalhadores que teríamos que selecionar em cada departamento atendendo a um critério de proporcionalidade?
1 Qual tipo de amostragem devemos utilizar para realizar a amostra se queremos que sejam incluídos trabalhadores dos quatro departamentos mencionados? Utilizaremos uma amostragem aleatória estratificada, pois, já que queremos que haja representantes de cada um dos departamentos, pegamos uma amostra significativa que representa a proporção de trabalhadores que há em cada departamento.
2 Qual o número de trabalhadores que teríamos que selecionar em cada departamento atendendo a um critério de proporcionalidade?
Para podermos selecionar uma quantidade proporcional de cada departamento, primeiro devemos conhecer a proporção que terá o tamanho da amostra em relação ao total de trabalhadores, ou seja:
Onde
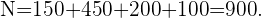
Agora, a quantidade de trabalhadores que vamos selecionar de cada departamento deve manter a proporção que calculamos, ou seja, o número 
de trabalhadores em cada departamento deve cumprir:
Então teremos
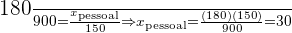
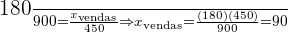
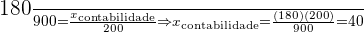
Além do mais, podemos constatar que
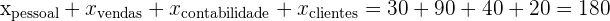
que é justamente o tamanho da amostra.
Intervalo de confiança
A quantidade de hemoglobina no sangue de um homem está em uma taxa normal, com uma desviação típica de 2g/dl. Calcule o intervalo de confiança de uma amostragem com 12 amostras de sangue que indique que a média de hemoglobina no sangue está entre 13 e 15 g/dl.
1 Precisamos encontrar o intervalo de confiança para que a média do nível de hemoglobina no sangue esteja entre 13 e 15 g/dl. Para fazer isso precisamos conhecer o nível de significância estatística e isso podemos saber através da fórmula do erro padrão, que 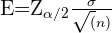é 
onde 
é o desvio padrão, 
é o tamanho da amostra e 
é o valor de uma distribuição normal padrão, em que 
Como queremos conhecer o intervalo de confiança da média entre 13 e 15 g/dl, pegamos o intervalo como estimativa para o erro padrão. Substituindo os valores na fórmula teremos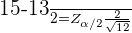
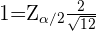Isolamos
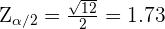Conhecendo já o valor de podemos calcular a probabilidade correspondente. Antes fazíamos isso com o uso de tabelas, porém hoje em dia temos ferramentas mais fáceis de utilizar, como o Wolfram. Assim, sabemos que a probabilidade é
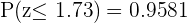
Dado que calculamos , é preciso subtrair a probabilidade do extremo esquerdo da distribuição normal, para isso consideramos
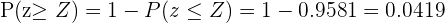
então,
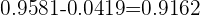
Portanto, o intervalo de confiança de que a média de hemoglobina no sangue esteja entre 15 e 13 g/dl é de 91.62% para uma amostragem com 12 amostras de sangue.
Teste de hipótese bicaudal
Um fabricante de lâmpadas elétricas está testando um novo método de produção que será aceito se as lâmpadas feitas com esse método possuam uma duração média de 2400 horas com um desvio padrão igual a 300. É realizada uma amostra com 100 lâmpadas produzidas com esse método da qual a duração média foi de 2320 horas. Podemos aceitar a hipótese de validez do novo processo de fabricação com um risco igual ou menor a 5%?
1 Este é um exercício onde temos que fazer um teste de hipótese. O objetivo é saber se a amostra é evidência suficiente para afirmar que o novo método de produção produzirá lâmpadas com uma duração média de 2400 horas e desvio padrão de 300 horas com uma taxa de 5% probabilidade ou menos. O primeiro passo é estabelecer a hipótese nula (
) e a hipótese alternativa (
), onde geralmente o resultado nos levará a aceitar ou não a hipótese nula.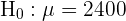
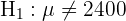Para fazer o teste de hipótese precisaremos calcular a estatística. Já que estamos supondo que o tempo de duração é distribuído de acordo com uma distribuição normal e o tamanho da amostra é igual a 100, vamos usar a estatística Z (variável aleatória de uma Normal padrão), que é
onde 
é a média da amostra, 
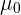é a média de 
, é desvio padrão e é o tamanho da amostra. Substituindo os valores temos
Agora calculamos o p-valor para 
, já que a hipótese alternativa é uma negação (
) essa é uma análise bicaudal, neste caso o p-valor é calculado como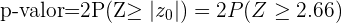
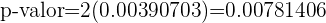
A probabilidade de erro é de 5%, o que quer dizer que o nível de significância que está sendo considerado é de 0,05 e sabemos que p-valor=0.0078; a hipótese nula é descartada se p-valor é menor que o valor de significância que é justamente o que temos
$$0.0078 < 0.05$$[/latex]
Portanto, há evidência suficiente para descartar a hipótese de que o novo método de produção produz lâmpadas com uma duração média de 2400 horas e desvio padrão de 300 com 5% probabilidade de equívoco.
O controle de qualidade de uma fábrica de pilhas e baterias suspeita que houve defeitos na produção de uma modelo de bateria para celulares, baixando assim seu tempo de duração. Até então, o tempo de duração de uma conversa tinha uma distribuição normal com média de 300 minutos e desvio padrão de 30 minutos. No entanto, em uma inspeção do último lote produzido, antes de ser enviado para o mercado, foi descoberto que, de uma amostra de 60 baterias, o tempo médio de duração de conversa foi de 290 minutos. Supondo que esse tempo continue sendo Normal, com o mesmo desvio padrão, poderíamos concluir que as suspeitas do controle de qualidade estariam corretas, com um nível de significância de 1%?
1 Neste exercício temos que fazer um teste de hipótese. O objetivo é saber se a amostra é evidência suficiente para afirmar com 1% de probabilidade de equívoco que a suspeita da equipe de controle de qualidade está correta em relação a diminuição da qualidade das baterias. O primeiro passo é estabelecer a hipótese nula () e a hipótese alternativa (), onde geralmente o resultado nos levará a descartar ou não a hipótese nula.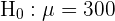
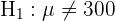Para fazer o teste de hipótese precisaremos calcular a estatística, já que estamos supondo que o tempo de duração é distribuído de acordo com uma distribuição normal e o tamanho da amostra é igual a 60. Usaremos a estatística Z (variável aleatória de uma Normal padrão), que édo qual é a média da amostra, 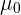é a média de , é o desvio padrão e é o tamanho da amostra. Substituindo os valores, temos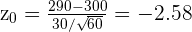 
Agora calcularemos o p-valor para 
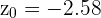, já que a hipótese alternativa é uma negação. () Esta é uma análise bicaudal, neste caso o p-valor é calculado como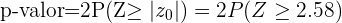
A probabilidade de erro é de 1%, o que quer dizer que o nível de significância que está sendo considerado é de 0,01 e sabemos que p-valor=0.0098; A hipótese nula é descartada se p-valor é menor que o valor de significância, que é justamente o que temos
$$0.0098 < 0.01$$[/latex]
Portanto, há evidência suficiente para descartar a hipótese de que a duração média da bateria é de 300 minutos com desvio padrão de 30 minutos com 1% de probabilidade de equívoco, com uma amostra de 60 baterias, ou seja, podemos concluir que as suspeitas da equipe de controle de qualidade estão corretas.
Acredita-se que o nível médio de protrombina em uma população normal é de 20 mg/100 ml de plasma com um desvio padrão de 4 miligramos/100 ml. Para comprovar é tirada uma amostra de 40 indivíduos, dos quais a média é de 18.5 mg/100 ml. Poderíamos confirmar essa hipótese com um nível de significância de 5%?
1 Este é um exercício onde temos que fazer um teste de hipótese. O objetivo é saber se a amostra é evidência suficiente para afirmar com 5% de probabilidade de equívoco que o nível médio de protrombina é de 20 mg/100 ml de plasma com um desvio padrão de 4 mg/100 ml. O primeiro passo é estabelecer a hipótese nula () e a hipótese alternativa (), onde geralmente o resultado nos levará a descartar ou não a hipótese nula.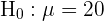
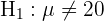Para fazer o teste de hipótese precisaremos calcular a estatística, já que estamos supondo que o tempo de duração é distribuído de acordo com uma distribuição normal e o tamanho da amostra é igual a 40. Usaremos a estatística Z (variável aleatória de uma Normal padrão), que édo qual é a média da amostra, 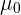é a média de , é o desvio padrão e é o tamanho da amostra. Substituindo os valores, temos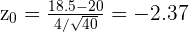
Agora calcularemos o p-valor para 
, já que a hipótese alternativa é uma negação. () Esta é uma análise bicaudal, neste caso o p-valor é calculado como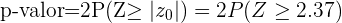
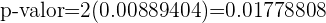
A probabilidade de erro é de 5%, o que quer dizer que o nível de significância que está sendo considerado é de 0.05 e sabemos que p-valor=0.0177; A hipótese nula é descartada se p-valor é menor que o valor de significância, que é justamente o que temos
$$0.0177 < 0.05$$[/latex]
Portanto, há evidência suficiente para descartar a hipótese de que o nível médio de protrombina é de 20 mg/100 ml de plasma com um desvio padrão de 4 mg/100 ml, com um nível de significância de 5% em uma amostra de 40 indivíduos.
Gostou desse artigo? Deixe uma nota!
Loading...
