Temas

Integral definida
Dada uma função  e um intervalo
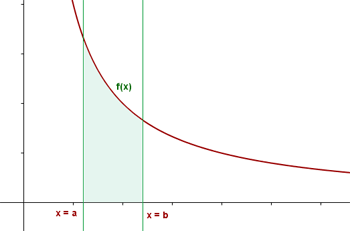
e um intervalo  , a integral definida é igual à área limitada entre o gráfico de
, a integral definida é igual à área limitada entre o gráfico de  , o eixo das abscissas e as retas verticais
, o eixo das abscissas e as retas verticais  e
e 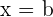 .
.
- A integral definida é representada por
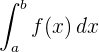 .
.  é o sinal de integração.
é o sinal de integração.- a é o limite inferior da integração.
- b é o limite superior da integração.
 é o integrando ou função a integrar.
é o integrando ou função a integrar. é diferencial de
é diferencial de  , e indica qual é a variável da função que é integrada.
, e indica qual é a variável da função que é integrada.
Propriedades da integral definida
1 O valor da integral definida muda de sinal se os limites de integração são permutados.
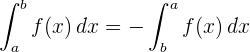
2 Se os limites que integram coincidem, a integral definida vale zero.

3 Se  é um ponto interior do intervalo
é um ponto interior do intervalo  , a integral definida é decomposta como uma soma de dois integrais estendidos nos intervalos
, a integral definida é decomposta como uma soma de dois integrais estendidos nos intervalos  e
e 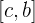 .
.
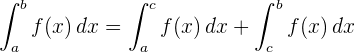
4 A integral definida de uma soma de funções é igual à soma de integrais.
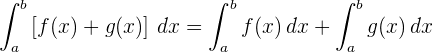
5 A integral do produto de uma constante por uma função é igual à constante pela integral da função.
Regra de Barrow
A regra de Barrow nos diz que a integral definida de uma função contínua  em um intervalo fechado
em um intervalo fechado  é igual à diferença entre os valores que toma uma função primitiva
é igual à diferença entre os valores que toma uma função primitiva 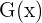 de
de  , nos extremos de tal intervalo.
, nos extremos de tal intervalo.
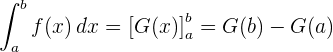
Teorema fundamental do cálculo
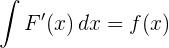
O Teorema fundamental do cálculo nos indica que a derivação e a integração são operações inversas.
Ao integrar uma função contínua e depois derivá-la, recuperamos a função original.
Teorema da média ou do valor médio para integrais
Se uma função é contínua em um intervalo fechado  , existe um ponto
, existe um ponto  no interior do intervalo, como:
no interior do intervalo, como:
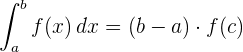
Função integral
Sendo 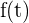 uma função contínua no intervalo
uma função contínua no intervalo  .
.
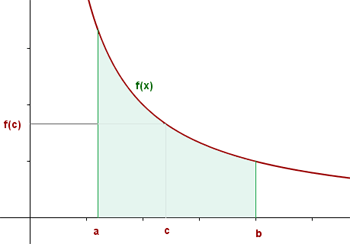
A partir desta função se define a função integral:

que depende do limite superior de integração.
Para evitar confusões quando fazemos referência à variável de  , chamamos ela de
, chamamos ela de  , mas se a referência é em relação à variável de
, mas se a referência é em relação à variável de  , chamamos ela de
, chamamos ela de  .
.
Geometricamente, a função integral,  , representa a área do espaço limitado pela curva
, representa a área do espaço limitado pela curva  , o eixo das abscissas e as retas
, o eixo das abscissas e as retas 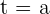 e
e 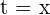 .
.
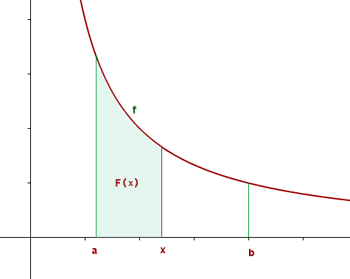
Também chamamos a função integral,  , de função de áreas de
, de função de áreas de  no intervalo
no intervalo  .
.
Resumir com IA:












