A integral definida é um caso da integral utilizado para determinar o valor das áreas delimitadas por um gráfico dentro de um intervalo e o eixo horizontal. Pode ser encontrada em diversas áreas e contextos, como a biologia (crescimento de populações), robótica (algoritmo de seguimento de linhas), arquitetura (volumes de sólidos), etc. Mais adiante será dado um exemplo específico de aplicação.
Formalmente define-se da seguinte maneira:
Definição da integral definida
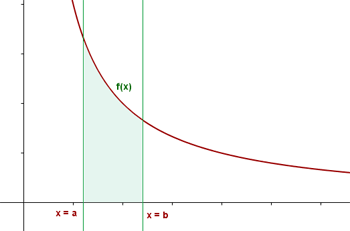
Dada uma função f(x) de uma variável real x e um intervalo [a,b] da reta real, a integral definida é igual à área limitada entre o gráfico de f(x), o eixo das abscissas, e as retas verticais x = a e x = b.
É representada por 
.
é o símbolo de integração.- a é o limite inferior da integração.
- b é o limite superior da integração.
é o integrando ou função a integrar.
é o diferencial de x e indica qual é a variável da função que se integra.
Propriedades da integral definida
1 O valor da integral definida muda de sinal se permutarmos os limites de integração.
Essa propriedade pode ser útil para evitar operar com sinais negativos.
Exemplo:
2 Se os limites de integração coincidirem, a integral definida vale zero.
Na verdade, ao ter o mesmo limite de integração em ambos os extremos não existe nenhuma área a calcular; por isso a integral é igual a zero nesse caso.
Exemplo:
3 Se c é um ponto interior do intervalo [a, b], a integral definida pode ser decomposta como soma de duas integrais estendidas aos intervalos [a, c] e [c, b].
Como o ponto c está entre a e b sobre o eixo das abscissas, a área limitada pelo intervalo [a,b] é a soma das áreas limitadas por [a,c] e [c,d], o mesmo vale para o valor da integral.
Exemplo:
Para 7 que pertence ao intervalo [3,10]
4 A integral definida da soma de funções é igual à soma das integrais.
Essa propriedade ajuda a evitar expressões muito longas dentro de uma mesma integral, permitindo manipular e calcular de modo mais simples, ou, alternativamente, agrupar termos para um cálculo mais conveniente.
Exemplo:
Para 
e 
,
5 A integral do produto de uma constante k por uma função é igual à constante k multiplicada pela integral da função.
Isto equivale a fatorar a constante para fora da integral.
Exemplo:
Para a constante k=3
Exemplo de aplicação
Neste exemplo aplicaremos as propriedades anteriores em uma aplicação da integral ao crescimento populacional, para melhor visualização.
Uma população cresce com uma taxa de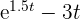 
indivíduos por ano (onde 
é número de anos). No primeiro ano a população é de 1500 pessoas.
Quanto cresceu a população entre o primeiro e o terceiro ano? Qual é a população no terceiro ano?
1 Como nos pedem o crescimento entre 1 e 3, isto é, a área sob a curva da taxa de crescimento entre 1 e 3, expressamos:
Nota: os passos a seguir ilustram o uso das propriedades; alguns deles podem ser omitidos.
2 Nos cálculos, observamos que podemos usar a propriedade 4 e separar em soma:
3 Também podemos usar a propriedade 5 e tirar a constante -3 que multiplica t:
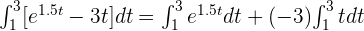
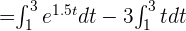
4 Dado que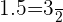 
substituímos e efetuamos os cálculos correspondentes para responder à primeira pergunta:
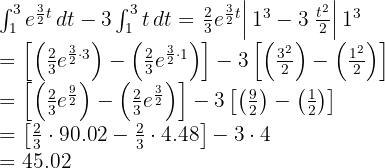
Assim, o crescimento entre o primeiro e o terceiro ano foi de 33 indivíduos aproximadamente.
5 Para a segunda pergunta seguimos o seguinte raciocínio:
- No ano 1 a população era de 1000 indivíduos.
- O crescimento entre o ano 1 e 3 foi de 33 indivíduos aproximadamente.
- Assim, a população no ano 3 é de 1033 indivíduos aproximadamente.
Gostou desse artigo? Deixe uma nota!
Loading...
