
Fórmula da integração por partes
Introdução
Ao contrário das derivadas, não existe uma fórmula que possa ser usada para integrar qualquer produto de funções.
A regra mais próxima que temos para integrar o produto de funções é a integração por partes. Curiosamente, ela é baseada na fórmula para derivar um produto de funções.
Entretanto, a integração por partes transforma uma integral de um produto em outra integral. Essa fórmula não funciona para integrar todos os produtos de funções.
A fórmula da integração por partes é:

Observe que temos que derivar  e integrar
e integrar  , por isso será conveniente que a integral de
, por isso será conveniente que a integral de  seja simples.
seja simples.
Em geral, as funções polinômicas, logarítmicas e arcotangente são escolhidas como  . enquanto as funções exponenciais, seno e cosseno são escolhidas como
. enquanto as funções exponenciais, seno e cosseno são escolhidas como  .
.
Demonstração da Fórmula
Vamos supor que são essas as funções:  e
e  . Então, sua derivada é dada por:
. Então, sua derivada é dada por:

Ao integrar os dois lados da equação, obtemos:
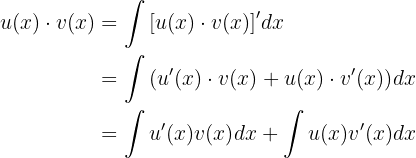
Agora, se passarmos  para o lado esquerdo, obtemos:
para o lado esquerdo, obtemos:

E esta é a fórmula que procurávamos.
Exercícios propostos

Temos um produto entre a função 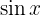 e
e  . Como mencionado anteriormente, neste tipo de caso, escolhemos
. Como mencionado anteriormente, neste tipo de caso, escolhemos 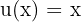 e
e 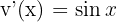 .
.
Fazendo a derivada  :
:
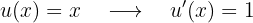
Agora, integramos  :
:
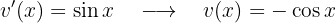
Portanto, a integral se torna:
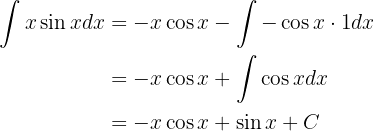
Ou seja,
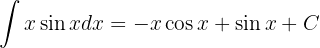

Temos um produto entre a função  e
e  . Neste tipo de caso, escolhemos
. Neste tipo de caso, escolhemos 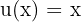 e
e  .
.
Fazemos a derivada  :
:
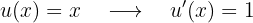
Agora, integramos  :
:

Portanto, a integral se torna:
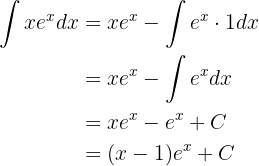
Dessa forma:
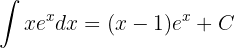
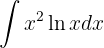
Temos um produto entre a função 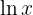 e
e  . Em geral, ambas as funções são normalmente escolhidas como
. Em geral, ambas as funções são normalmente escolhidas como  . No entanto, neste tipo de caso, o logaritmo tem preferência e escolhemos
. No entanto, neste tipo de caso, o logaritmo tem preferência e escolhemos  e
e 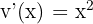 .
.
Fazemos a derivada  (este é o motivo pelo qual escolhemos o logaritmo):
(este é o motivo pelo qual escolhemos o logaritmo):
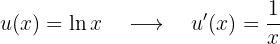
Agora, integramos  :
:
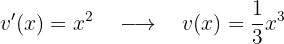
Portanto, a integral se torna:
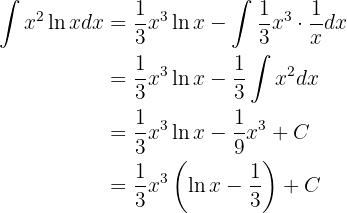
Dessa forma:
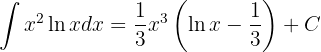
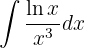
Temos um produto entre a função 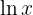 e
e 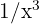 . Novamente, neste tipo de caso, escolhemos
. Novamente, neste tipo de caso, escolhemos  e
e 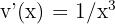 (a função logaritmo é sempre escolhida como
(a função logaritmo é sempre escolhida como  ).
).
Derivamos  :
:
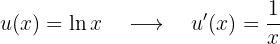
Agora, integramos  :
:
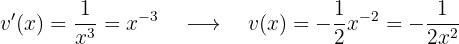
Portanto, a integral se torna:
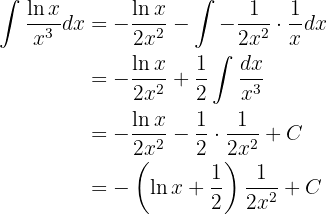
Ou seja:
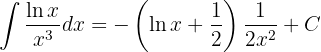
Resumir com IA:












