Temas

Identidades trigonométricas fundamentais
1. Relação entre seno e cosseno
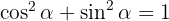
2. Relação entre secante e tangente
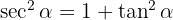
3. Relação entre cossecante e cotangente

4. Funções trigonométricas recíprocas
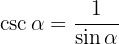
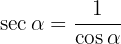

Exemplos de exercícios com identidades trigonométricas fundamentais
Sabendo que 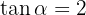 , e que
, e que  180^{\circ}< \alpha < 270^{\circ}[/latex], calcule as demais razões trigonométricas do ângulo [latex] \alpha [/latex].
180^{\circ}< \alpha < 270^{\circ}[/latex], calcule as demais razões trigonométricas do ângulo [latex] \alpha [/latex].
Vamos obter as demais funções trigonométricas avaliadas neste ângulo.
Começaremos com  já que podemos obtê-la diretamente de
já que podemos obtê-la diretamente de 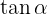 .
.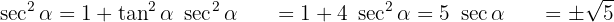
No entanto, podemos notar que para o quadrante (ou intervalo) onde  está definido, temos
está definido, temos 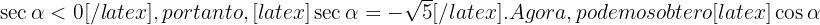 .
.
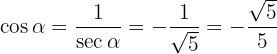
Vamos obter o 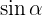 e, com isso o
e, com isso o 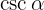 .
.
Como 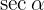 , sabemos que o seno é negativo para o quadrante no qual
, sabemos que o seno é negativo para o quadrante no qual  está definido, logo:
está definido, logo:

Agora que já temos 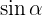 , e percebemos que:
, e percebemos que:
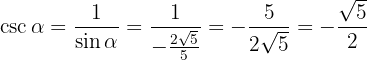
Por fim, vamos obter  .
.
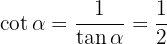
Sabendo que 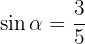 , e que
, e que  90^{\circ}< \alpha< 180^{\circ}[/latex], calcule as demais razões trigonométricas do ângulo [latex] \alpha [/latex].
90^{\circ}< \alpha< 180^{\circ}[/latex], calcule as demais razões trigonométricas do ângulo [latex] \alpha [/latex].
Vamos obter as demais funções trigonométricas avaliadas neste ângulo. Começaremos com 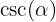 já que podemos obtê-la diretamente.
já que podemos obtê-la diretamente.

Agora podemos obter o 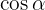 . Note que, pelo intervalo no qual
. Note que, pelo intervalo no qual  está definido, o cosseno será negativo, logo:
está definido, o cosseno será negativo, logo:
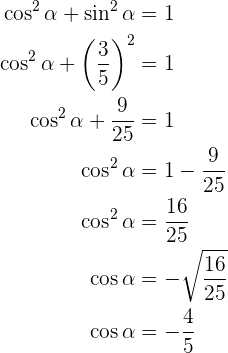
Uma vez que temos o cosseno, podemos obter 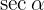 diretamente:
diretamente:

Agora, falta calcular a tangente e a cotangente, que podemos obter a partir do seno e cosseno:

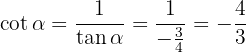
Razões trigonométricas da soma e diferença de ângulos
1. 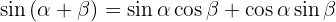
2. 
3. 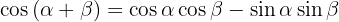
4. 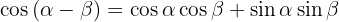
5. 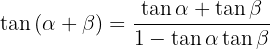
6. 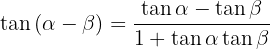
Exemplos de exercícios de soma e diferença de ângulos
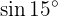
Para resolver este exercício, vamos expressar o ângulo como a soma de dois ângulos específicos, permitindo o uso das fórmulas das funções trigonométricas para soma e subtração de ângulos.
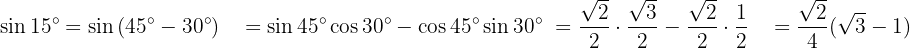

Para resolver este exercício, vamos expressar o ângulo como a soma de dois ângulos específicos, permitindo o uso das fórmulas das funções trigonométricas para soma e subtração de ângulos.
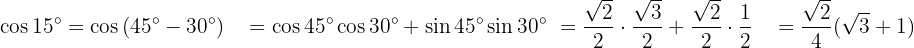
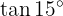
Para resolver este exercício, vamos expressar o ângulo como a soma de dois ângulos específicos, permitindo o uso das fórmulas das funções trigonométricas para soma e subtração de ângulos.
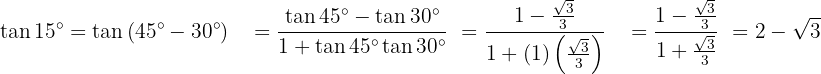
Razões trigonométricas do ângulo duplo
1. 
2. 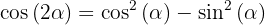
3. 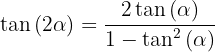
Exemplos de exercícios com ângulo duplo
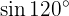
Para resolver este exercício, primeiro determinaremos a metade do ângulo dado e, em seguida, aplicaremos a fórmula correspondente da função trigonométrica do ângulo duplo.

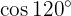
Para resolver este exercício, primeiro determinaremos a metade do ângulo dado e, em seguida, aplicaremos a fórmula correspondente da função trigonométrica do ângulo duplo:
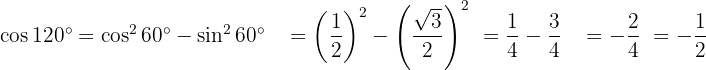
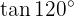
Para resolver este exercício, primeiro encontraremos a metade do ângulo dado para, então, utilizar a fórmula da função trigonométrica de ângulo duplo correspondente:
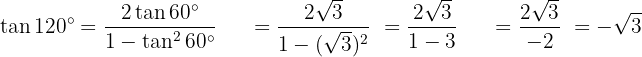
Razões trigonométricas do meio ângulo
1. 
2. 
3. 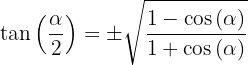
Exemplos de exercícios de meio ângulo
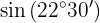
Para resolver este exercício, primeiro vamos encontrar o dobro do ângulo dado e depois aplicar a fórmula da função trigonométrica correspondente. Podemos notar que, dado o quadrante em que o ângulo está, o valor do seno será positivo.
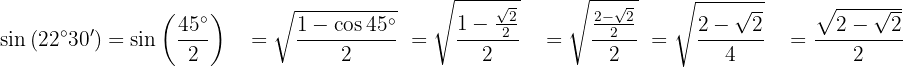

Para resolver este exercício, primeiro encontramos o dobro do ângulo dado e, em seguida, aplicamos a fórmula correspondente à função trigonométrica. Como o ângulo está em um quadrante onde o cosseno é positivo, esse será o sinal do resultado.
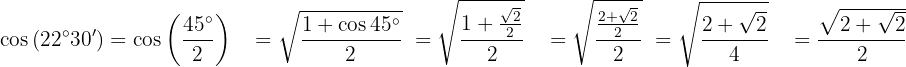
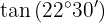
Para resolver este exercício, primeiro vamos encontrar o dobro do ângulo dado e depois aplicar a fórmula da função trigonométrica correspondente. Vamos notar que, pelo quadrante em que o ângulo está, o valor da tangente será positivo.
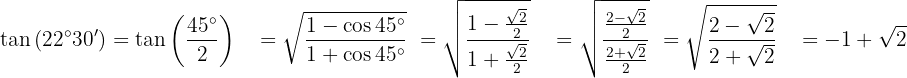
Transformação de operações
Transformações de somas em produtos
1. 
2. 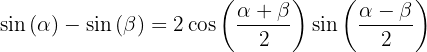
3. 
4. 
Exemplos de transformação de somas em produtos
Nos próximos exercícios, em vez de escrever o valor da soma ou diferença das funções trigonométricas, vamos apenas transformá-las em um produto de outras funções trigonométricas, seguindo a fórmula adequada.
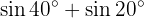
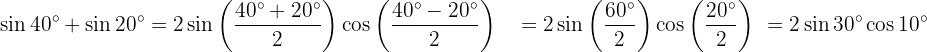
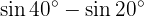
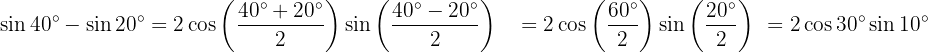
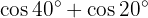
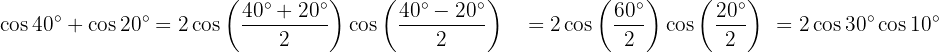
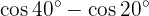
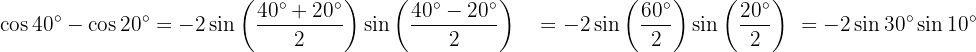
Transformações de produtos em somas
1. 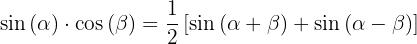
2. 
3. 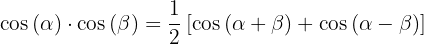
4. 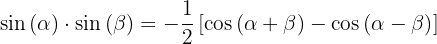
Exemplos de transformações de produtos em somas
Nos próximos exercícios, em vez de escrever o valor da multiplicação das funções trigonométricas, vamos transformá-la em uma soma ou subtração de outras funções trigonométricas, de acordo com a fórmula apropriada.
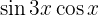
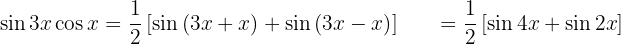
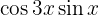
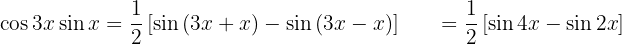
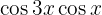
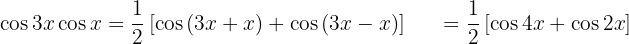

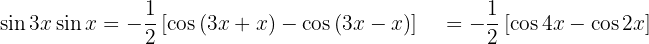
Resumir com IA:












