Temas

Identidades trigonométricas e suas propriedades
- Relação entre seno e cosseno
A principal identidade é: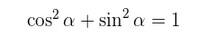
- Relação entre secante e tangente
A relação fundamental é: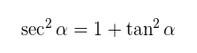
- Relação entre cossecante e cotangente
A identidade correspondente é: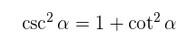
- Funções trigonométricas recíprocas
As definições recíprocas são: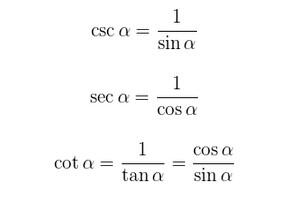
Exemplos de exercícios de identidades trigonométricas
Sabe-se que tan α = 2 e que 180° < α < 270°, calcule as razões trigonométricas restantes de um ângulo α. Vamos obter as demais funções trigonométricas do ângulo dado. Vamos começar pelo sec α já que através dele podemos obter diretamente a tan α: E podemos observar que, para o quadrante (ou intervalo) onde está definido α, temos que sen(α) < 0. Com o seno determinado, podemos obter o cos(α) Com isso, podemos obter o seno (α) e o cosseno (α), da mesma forma que o secante(α), se o seno (α) é negativo para o quadrante no qual α está definido, assim: Agora, podemos aplicar: E, por fim, vamos obter ao cot (α): Sabe-se que Vamos começar os cálculos das demais funções trigonométricas, começando pelo csc α: Assim, seguiremos para descobrir o cos α, e podemos notar que o intervalo onde está definido α o cosseno é negativo. Portanto: Com o cosseno definido, partimos para o sec α: E obter a tangente e a cotangente, a partir do seno e cosseno: 
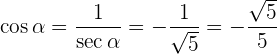
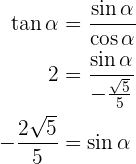
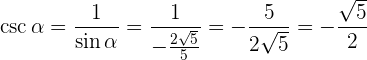
![]()
![]() , y que
, y que ![]() , calcule as razões trigonométricas restantes do ângulo α.
, calcule as razões trigonométricas restantes do ângulo α.
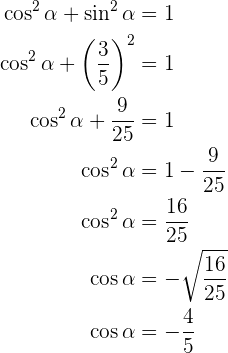
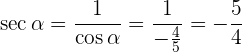

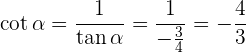
Razões trigonométricas da soma e diferença de ângulos
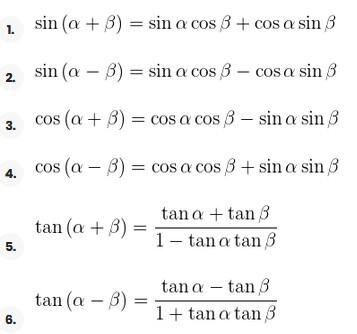
Exemplos de exercícios de soma e diferença de ângulos
Seno 15° Para resolver este exercício, escreveremos o ângulo como a soma de dois ângulos específicos, o com o objetivo de utilizar as fórmulas das funções trigonométricas aplicadas na soma e subtração de ângulos. Cosseno 15° Para resolver este exercício, vamos escrever o ângulo como a soma de dois ângulos específicos, com o objetivo de usar as fórmulas das funções trigonométricas aplicadas à soma e subtração de ângulos. Tangente 15° Para resolver este exercício, vamos escrever o ângulo como a soma de dois ângulos específicos, com o objetivo de aplicar as fórmulas das funções trigonométricas utilizadas na soma e subtração de ângulos.

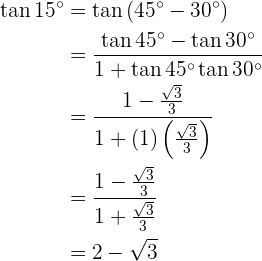
Razões trigonométricas do ângulo duplo
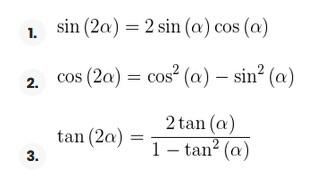
Exemplos de exercícios com ângulo duplo
Sen 120° Para resolver este exercício, primeiro encontraremos a metade do ângulo dado e, posteriormente, utilizaremos a fórmula da função trigonométrica do ângulo duplo correspondente. Cos 120° Para resolver este exercício, primeiro encontraremos a metade do ângulo dado e, em seguida, utilizaremos a fórmula da função trigonométrica do ângulo duplo correspondente. Tan 120° Para resolver este exercício, primeiro encontraremos a metade do ângulo dado e, posteriormente, utilizaremos a fórmula da função trigonométrica do ângulo duplo correspondente.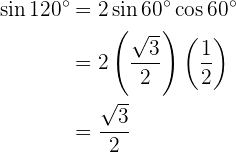
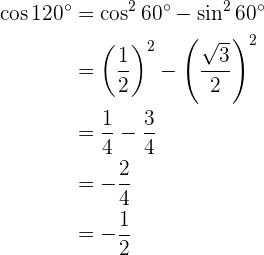
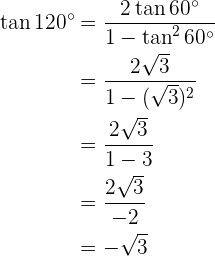
Razões trigonométricas do arco metade
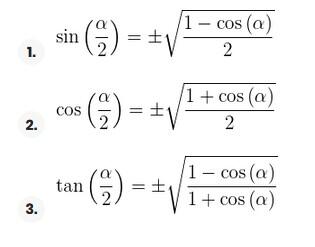
Exemplos de exercícios de arco metade
Seno (22°30')
Para resolver este exercício, primeiro obteremos o dobro do ângulo dado e, posteriormente, aplicaremos a fórmula correspondente à função trigonométrica indicada. Vamos observar que, de acordo com o quadrante em que o ângulo se encontra, o valor do seno será positivo.
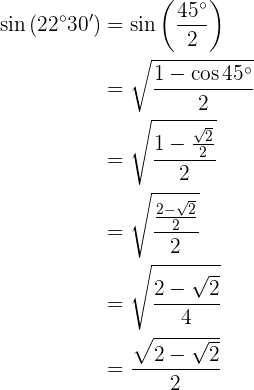
Cosseno (22°30')
Para resolver este exercício, primeiro obteremos o dobro do ângulo dado e, posteriormente, aplicaremos a fórmula correspondente à função trigonométrica indicada. Podemos observar que, de acordo com o quadrante em que o ângulo se encontra, o valor do cosseno será positivo.
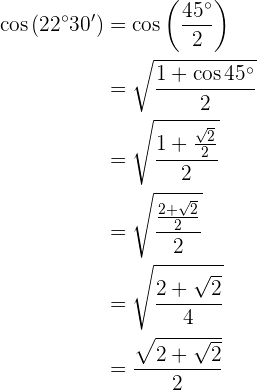
Tangente (22°30')
Para resolver este exercício, primeiro vamos obter o dobro do ângulo dado e, posteriormente, aplicaremos a fórmula correspondente à função trigonométrica indicada. Também podemos notar que, de acordo com o quadrante em que o ângulo se encontra, o valor da tangente será positivo.
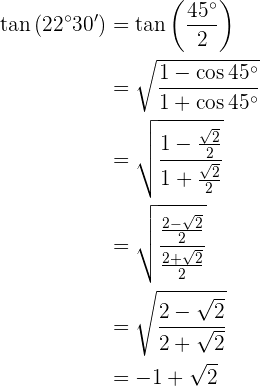
Transformação de operações
Transformações de somas em produtos
Nos próximos exercícios, não escreveremos o valor da soma ou diferença das funções trigonométricas, simplesmente as transformaremos em produtos de outras funções trigonométricas, conforme a fórmula que deve ser aplicada.
sen 40° + sen 20° sen 40° - sen 20° cos 40° + cos 20° cos 40° - cos 20°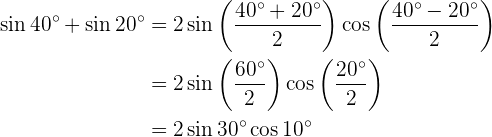
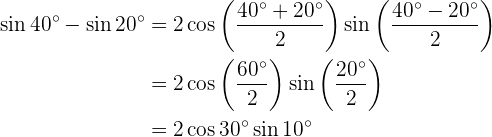
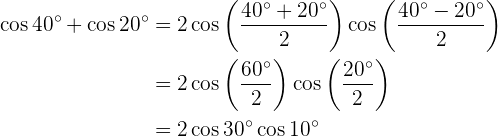
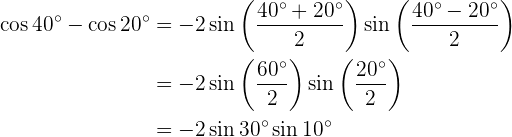
Transformação de produtos em somas
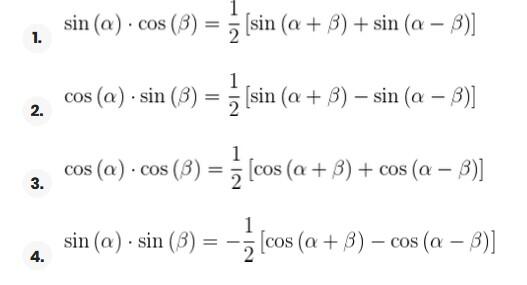
Exemplos de transformações de produtos em somas
Nos próximos exercícios, não escreveremos o valor da multiplicação das funções trigonométricas, simplesmente a transformaremos em soma ou diferença de outras funções trigonométricas, conforme a fórmula que deve ser aplicada.
sen 3x cos x cos 3x sen x cos 3x cos x sen 3x sen x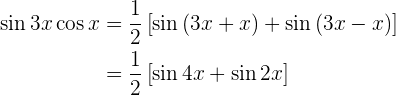
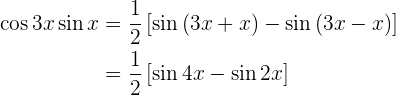
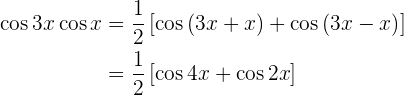
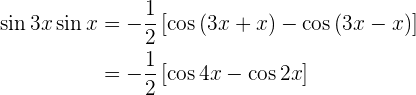
Resumir com IA:












