Uma equação exponencial é aquela em que a incógnita aparece no expoente.
Para resolver equações exponenciais, devemos lembrar das propriedades das potências:
As propriedades das potências
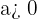
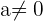
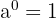
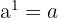
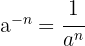
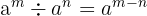
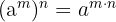
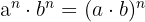
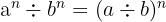
- si
entonces 
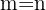
Resolução de equações exponenciais
Caso 1: Como expressar os dois membros da equação usando a mesma base
Fazemos as transformações necessárias até que ambos os membros tenham a mesma base e então igualamos os expoentes.
Exemplos
1 
Reescrevemos o lado direito como 
e decompomos o número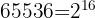 
Como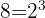 
, então:
Igualamos as potências:
2 
Transformamos as raízes em potências de exponente fracionário e igualamos los exponentes
Resolvemos a equação resultante:
3 
Extraímos fator comum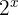 
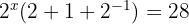
Aplicamos a lei da potência negativa e resolvemos as operações, isolando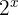
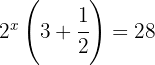
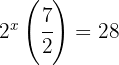
Reescrevemos a equação com a mesma base e igualamos os expoentes:
Caso 2: A soma dos termos de uma progressão geométrica
Se temos a soma dos 
termos de uma progressão geométrica, aplicamos a fórmula:
Exemplo
Aplicando a fórmula da soma dos termos de uma progressão geométrica:
Isolamos 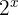e expressamos ambos os membros com a mesma base.
Caso 3: Mudança de variável
Quando temos uma equação mais complexa podemos recorrer a uma mudança de variável.
Exemplos
1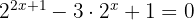 
Em primeiro lugar aplicamos a propriedade do produto de potências para eliminar a soma no expoente:
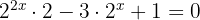
Aplicamos a propriedade de potência de uma potência:
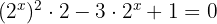
Realizamos a mudança de variável 
Fatorando a equação e resolvendo:
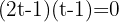
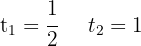
Desfazemos a mudança de variável:
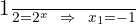
2 
Aplicamos as propriedades das potências do produto ou do quociente para eliminar as somas ou subtrações nos expoentes.
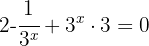
Fazemos a mudança de variável 
Multiplicamos ambos os membros por 
Fatoramos e resolvemos a equação:
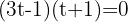
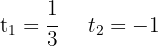
Desfazemos a mudança de variável:
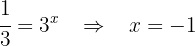
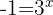
Da segunda equação não obtemos solução.
3 
Decompomos em fatores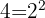 
e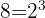
Realizamos a mudança de variável:
Desfazemos a mudança de variável apenas com a solução positiva:
Como não podemos igualar expoentes, tomamos logaritmos nos dois membros e no primeiro membro aplicamos a propriedade:
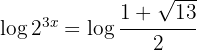
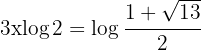
Isolamos 
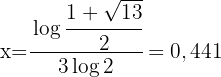
Para a outra solução de sinal negativo não teríamos solução, porque ao aplicar logaritmos no segundo membro encontraríamos o logaritmo de um número negativo, que não existe.
Caso 4: Não se podem expressar ambos os membros com a mesma base
Para isolar uma incógnita que está no expoente de uma potência, tomamos logaritmos cuja base é a base da potência.
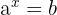
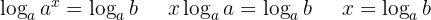
Exemplo
1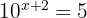 
Pegando os logaritmos nos dois membros:
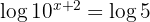
Aplicamos a propriedade do logaritmo de uma potência:
Como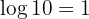 
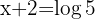
Isolamos
Gostou desse artigo? Deixe uma nota!
Loading...
