Temas
- Razões trigonométricas
- Identidades trigonométricas
- Identidades da soma e diferença de ângulos
- Identidades do arco duplo e do arco metade
- Identidades para a redução de potências
- Transformação de soma em produto e vice-versa
- Teoremas do seno, do cosseno e da tangente
- Fórmulas para calcular a área de um triângulo

Razões trigonométricas
Vamos observar s o seguinte triângulo retângulo:
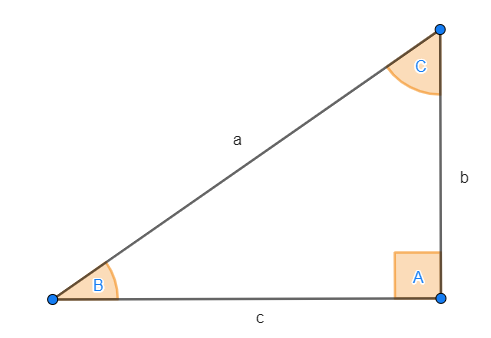
As razões ou funções trigonométricas para o ângulo  são definidas da seguinte maneira:
são definidas da seguinte maneira:
1 Seno:
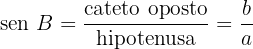
Vamos observar que, em algumas ocasiões, o seno é denotado como 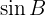 .
.
2 Cosseno:
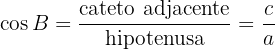
3 Tangente:
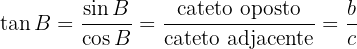
A tangente, em algumas ocasiões, é denotada como 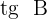 .
.
4 Cotangente:
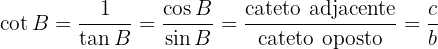
A cotangente, em algumas ocasiões, é denotada como 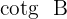 .
.
5 Secante:
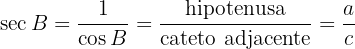
6 Cossecante:
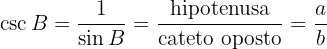
Em algumas ocasiões, a cossecante é denotada como 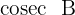 .
.
Nas identidades seguintes utilizaremos  e
e  para denotar ângulos (em lugar de
para denotar ângulos (em lugar de  ,
,  ou
ou  ).
).
Identidades trigonométricas
Vamos lembrar que uma identidade trigonométrica é uma relação que envolve funções trigonométricas e que satisfaz para todos os ângulos  do domínio. Essas identidades são muito úteis no momento de resolver integrais, equações diferenciais e outros problemas matemáticos.
do domínio. Essas identidades são muito úteis no momento de resolver integrais, equações diferenciais e outros problemas matemáticos.
Como as funções trigonométricas se definem a partir de triângulos retângulos, então satifazem as seguintes identidades:
1 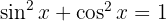
2 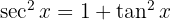
3 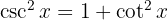
Identidades da soma e diferença de ângulos
1 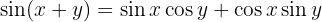
2 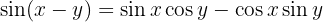
3 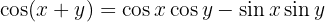
4 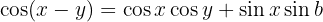
5 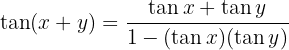
6 
Identidades do arco duplo e do arco metade
As identidades do arco duplo podem ser obtidas a partir das identidades da soma de ângulos (com  ). Por outro lado, as identidades do arco metade são obtidas a partir da identidade do ângulo duplo de
). Por outro lado, as identidades do arco metade são obtidas a partir da identidade do ângulo duplo de  .
.
Arco duplo
1 
2 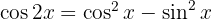
3 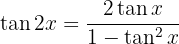
Arco metade
1 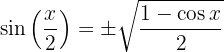
2 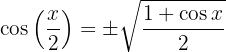
3 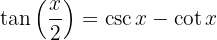
Observamos que a tangente do arco metade também satisfaz as seguintes identidades:

e
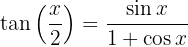
Identidades para a redução de potências
1 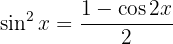
2 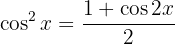
Transformação de soma em produto e vice-versa
Transformação de soma em produto
1 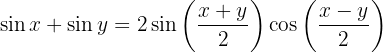
2 
3 
4 
5 
Transformação de produto em soma
1 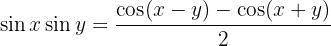
2 
3 
4 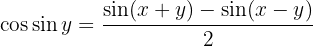
Teoremas do seno, do cosseno e da tangente
Os teoremas do seno, do cosseno e da tangente permitem calcular lados ou ângulos desconhecidos quando o triângulo não é retângulo. Observe a seguinte figura:
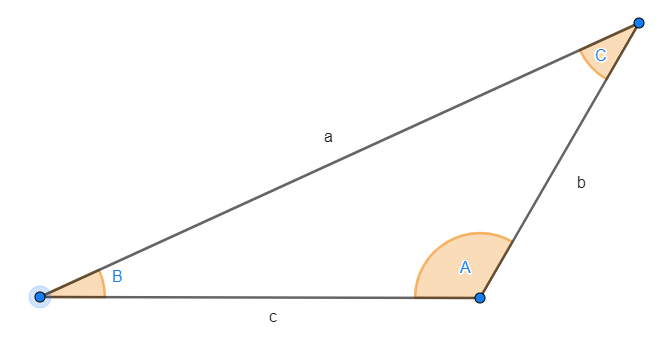
1 Teorema do seno: Dado um triângulo (não necessariamente retângulo) com lados  ,
,  e
e  , com seus ângulos opostos
, com seus ângulos opostos  ,
,  e
e  , satisfaz a:
, satisfaz a:

Nota: se conhecemos dois ângulos e um lado, então usamos o teorema do seno para calcular os dois lados restantes (o ângulo faltante se calcula lembrando que a soma dos ângulos é  ).
).
2 Teorema do cosseno: Dado um triângulo (não necessariamente retângulo) com lados  ,
,  e
e  , com seus ângulos opostos
, com seus ângulos opostos  ,
,  e
e  , satisfaz a:
, satisfaz a:
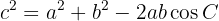
De maneira análoga, também satisfaz a:
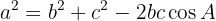
e
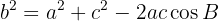
Nota: se conhecemos a medida dos três lados, usamos o teorema do cosseno para calcular os ângulos. Da mesma forma, se conhecemos dois lados e o ângulo formado entre eles, usamos o teorema do cosseno para calcular os dois ângulos restantes e o terceiro lado.
3 Teorema da tangente: Dado um triângulo (não necessariamente retângulo) com lados  ,
,  e
e  , com seus ângulos opostos
, com seus ângulos opostos  ,
,  e
e  , satisfaz a:
, satisfaz a:

Fórmulas para calcular a área de um triângulo
Por fim, apresentamos algumas fórmulas para calcular a área de um triângulo. Nessas fórmulas a área é denotada por  :
:
1 Se  é a base e
é a base e  a altura (perpendicular à base
a altura (perpendicular à base  ), então a área é calculada por:
), então a área é calculada por:
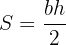
2 Vamoa considerar um triângulo com lados  ,
,  e
e  , com ângulos opostos
, com ângulos opostos  ,
,  e
e  , então, área pode ser calculada utilizando:
, então, área pode ser calculada utilizando:

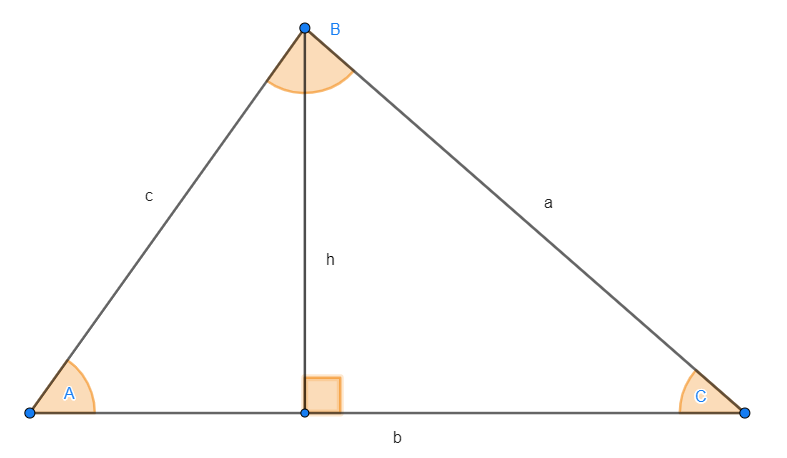
Na figura seguinte observamos a altura perpendicular a  , desse ponto, é possível ver claramente que
, desse ponto, é possível ver claramente que 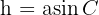 , de onde se deduz a fórmula.
, de onde se deduz a fórmula.
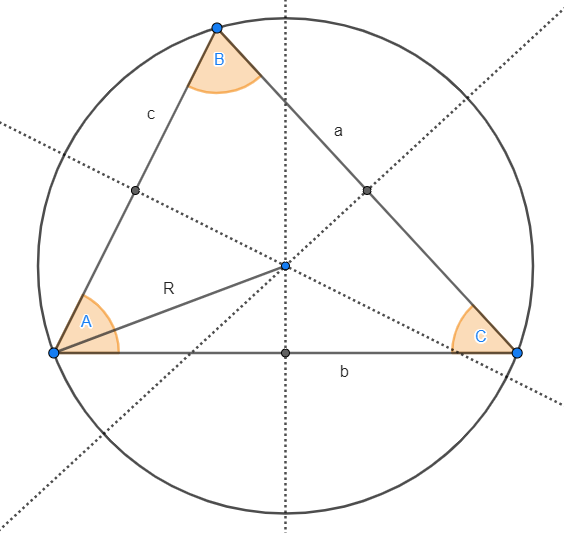
3 Se  é o raio da circunferência circunscrita, então a área se calcula por:
é o raio da circunferência circunscrita, então a área se calcula por:

Na figura seguinte observamos a circunferência circunscrita, com raio denotado por:  .
.
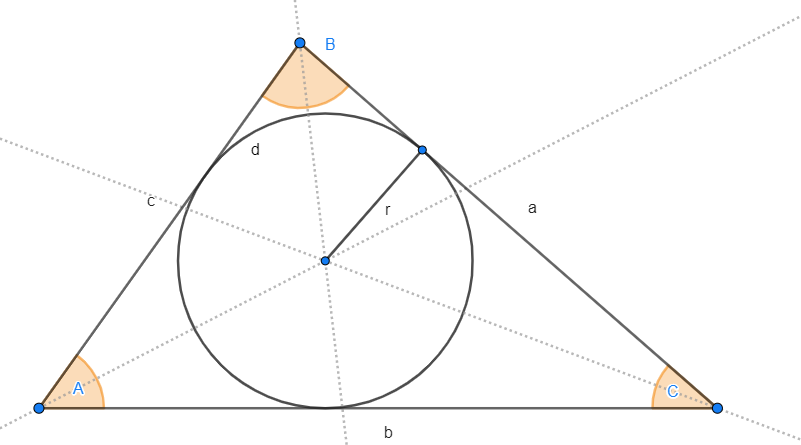
4 Se  é o raio da circunferência inscrita (inraio), então a área é calculada por:
é o raio da circunferência inscrita (inraio), então a área é calculada por:
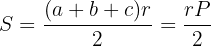
onde  denota o perímetro do triângulo.
denota o perímetro do triângulo.
Na figura seguinte observamos a circunferência inscrita, cujo raio é denotado por:  .
.
5 Fórmula de Heron: Seja 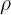 o semiperímetro do triângulo de lados
o semiperímetro do triângulo de lados  ,
,  e
e  , ou seja,
, ou seja,
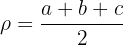
então a área é calculada por:
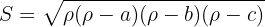
Resumir com IA:












