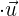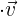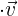Bem vindos aos emocionantes exercícios de vetores e produto escalar ! Os vetores são ferramentas fundamentais no campo das matemáticas e da física utilizados para representar magnitudes direcionais no plano e no espaço. São úteis quando queremos descobrir movimentos, forças, velocidades e muitas outras quantidades físicas.
Nestes exercícios, você vai explorar a manipulação de vetores e vai aprender a realizar operações importantes, como a soma e a subtração de vetores. Também irá adentrar no emocionante mundo do produto escalar, uma operação que combina magnitudes e direções de dois vetores para obter um valor numérico.
Através de desafiantes problemas práticos, você vai colocar à prova suas habilidades e vai descobrir como estas ferramentas matemáticas são aplicáveis em diversas disciplinas, como engenharia, física, informática, gráficos computacionais e outras mais. Dito isso, prepare-se para desenvolver sua destreza na manipulação vetorial e a potencializar sua capacidade para resolver problemas complexos.
Encontre o simétrico do ponto 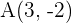 em relação a
em relação a 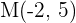 .
.
a) Calculamos o ponto simétrico  , para o qual usaremos
, para o qual usaremos 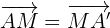

b) Igualamos as coordenadas e isolamos as variáveis 
Para a primeira coordenada:

Para a segunda coordenada:
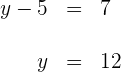
c) O simétrico  tem coordenadas
tem coordenadas
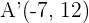
Dados dois vértices de um triângulo  e o baricentro
e o baricentro  , calcule o terceiro vértice.
, calcule o terceiro vértice.
a) A fórmula para o baricentro de um triângulo com vértices 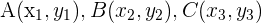 é:
é:

b) Calculamos o baricentro com o terceiro vértice 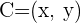 para o qual substituímos na fórmula anterior:
para o qual substituímos na fórmula anterior:
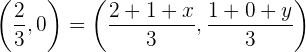
c) Igualamos as coordenadas e resolvemos para as variáveis 
Para a primeira coordenada:
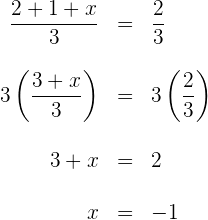
Para a segunda coordenada:
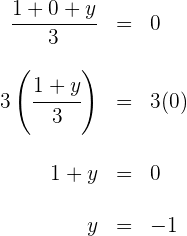
d) O terceiro vértice é:
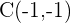
Dado os pontos  e
e 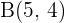 encontre um ponto
encontre um ponto  , alinhado com
, alinhado com  e
e  , de maneira que obtenhamos
, de maneira que obtenhamos 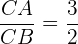
a) Como 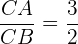 , substituímos os valores de
, substituímos os valores de  e
e 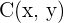 e obtemos:
e obtemos:
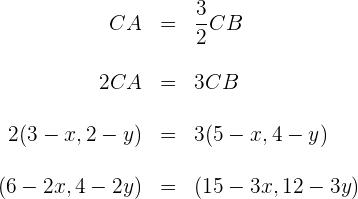
b) Igualamos as coordenadas e resolvemos para as variáveis 
Para a primeira coordenada:
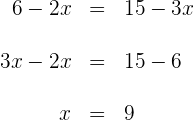
Para a segunda coordenada:
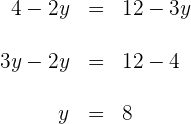
c) O ponto que procurávamos é 
Calcule as coordenadas de 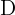 para que o quadrilátero dos vértices:
para que o quadrilátero dos vértices:  e
e 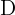 seja um paralelogramo.
seja um paralelogramo.
a) Para encontrar as coordenadas  utilizamos o fato de que os lados opostos do paralelograma por serem iguais, seus vetores também serão iguais:
utilizamos o fato de que os lados opostos do paralelograma por serem iguais, seus vetores também serão iguais:
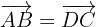
b) Substituímos os dados e obtemos:
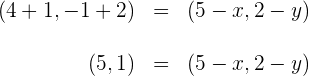
c) Igualamos as coordenadas e resolvemos para as variáveis 
Para a primeira coordenada:
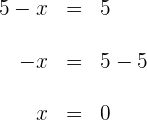
Para a segunda coordenada:
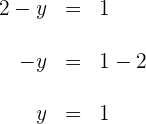
d) O vértice que procurávamos é 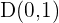
Se  formam uma base ortonormal, calcule:
formam uma base ortonormal, calcule:
Como  são ortonormais, então são perpendiculares entre si, dessa forma formam um ângulo de
são ortonormais, então são perpendiculares entre si, dessa forma formam um ângulo de  e sua magnitude é 1, isto é,
e sua magnitude é 1, isto é, 
Para encontrar os produtos solicitados utilizamos a fórmula:
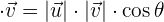
com  igual ao ângulo entre
igual ao ângulo entre  e
e 
Encontramos os produtos solicitados substituindo na fórmula e utilizando o valor adequado de  se é o vetor é o mesmo e
se é o vetor é o mesmo e  se são diferentes:
se são diferentes:
a) 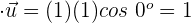
b) 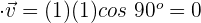
c) 
d) 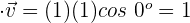
Dados os vetores  , calcule
, calcule  para que os vetores
para que os vetores  sejam:
sejam:
- Perpendiculares.
- Paralelos.
- Formem um ângulo de
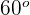 .
.
a) Perpendiculares: Dois vetores são perpendiculares se seu produto é zero
Realizamos o produto e isolamos a variável 
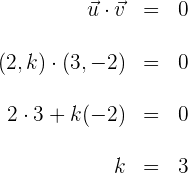
b) Paralelos: Dois vetores são paralelos se seus componentes são proporcionais, isto é,
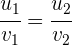
Realizamos a igualdade de proporções e isolamos a variável 
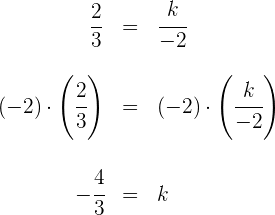
c) Formem um ângulo de 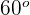 : Substituímos os valores na fórmula do produto de vetores
: Substituímos os valores na fórmula do produto de vetores
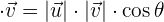
com 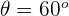
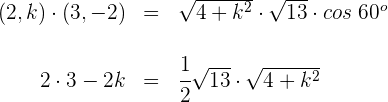
Elevamos ambos lados ao quadrado e simplificamos
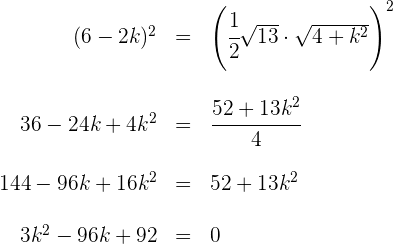
Resolvemos utilizando a fórmula para encontrar as raízes da equação do segundo grau
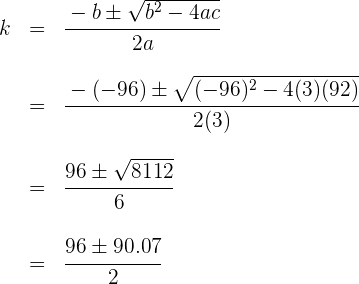
As raízes da equação quadrática são  , mas somente
, mas somente 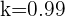 satisfaz a equação sem os quadrados, por isso este é o valor de
satisfaz a equação sem os quadrados, por isso este é o valor de  que procurávamos.
que procurávamos.
Calcule o valor de  sabendo que
sabendo que 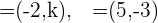 e
e 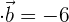
a) Calculamos o produto de vetores
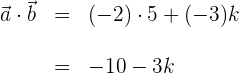
b) Igualamos o resultado em 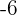 e resolvemos para
e resolvemos para 
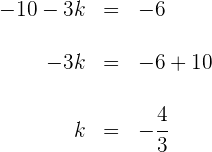
Supondo que em uma base ortonormal 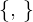 do plano. Calcule o valor
do plano. Calcule o valor  para que os vetores
para que os vetores 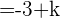 e
e 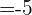 sejam ortogonais.
sejam ortogonais.
a) Como a base é ortonormal, então
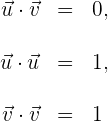
b) Calculamos o produto de  e
e 
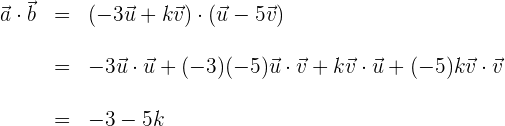
c) Dois vetores são ortogonais se seu produto escalar é zero. Substituímos e isolamos 
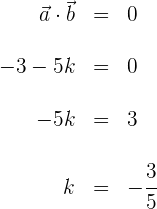
Calcule a projeção do vetor  sobre o vetor
sobre o vetor 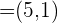 .
.
a) A fórmula da projeção do vetor  sobre o vetor
sobre o vetor  é dada por
é dada por
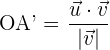
b) Calculamos o produto dos vetores
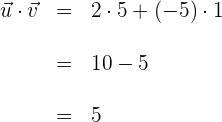
c) Calculamos a magnitude do vetor 
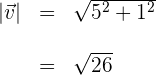
d) Substituímos os dados na fórmula da projeção
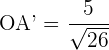
Encontre um vetor unitário  com uma mesma direção do vetor
com uma mesma direção do vetor 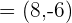 .
.
a) A fórmula de um vetor unitário é dada por:
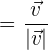
b) Calculamos a magnitude do vetor 
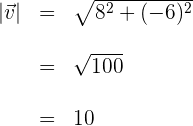
c) Substituímos na fórmula de vetor unitário:
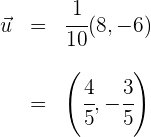
Resumir com IA: