Temas

Revisão
A partir da equação canônica da parábola, é fácil determinar muitos de seus elementos sem necessidade de fazer cálculos complicados. Da mesma forma, dados alguns dos elementos de uma parábola, podemos encontrar sua equação.
A seguir, apresentamos um resumo do que é mais importante saber sobre as parábolas.
Equação canônica ou ordinária:
1 
Tem abertura para a direita
Foco 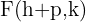
Diretriz 
2 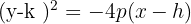
Tem abertura para a esquerda
Foco 
Diretriz 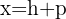
3 
Tem abertura para cima
Foco 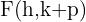
Diretriz 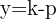
4 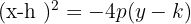
Tem abertura para baixo
Foco 
Diretriz 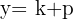
O vértice da parábola é o ponto 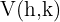 .
.
Quando a parábola tem o vértice na origem, ocorre o seguinte com sua equação:
1 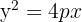
Tem abertura para a direita
Foco 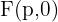
Diretriz 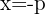
2 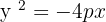
Tem abertura para a esquerda
Foco 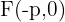
Diretriz 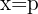
3 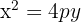
Tem abertura para cima
Foco 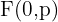
Diretriz 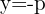
4 
Tem abertura para baixo
Foco 
Diretriz 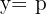
 representa a medida do lado reto ou LR.
representa a medida do lado reto ou LR. é a distância do vértice ao foco e do vértice à diretriz.
é a distância do vértice ao foco e do vértice à diretriz.
Descubra os elementos da parábola
Com base na equação das parábolas a seguir, esboce o gráfico da parábola:



A forma de proceder será determinar, na forma reduzida, as equações das parábolas, indicando o valor do parâmetro  , e com isso as coordenadas do foco e a equação da diretriz.
, e com isso as coordenadas do foco e a equação da diretriz.
1. 
Isolamos o termo quadrático:

Identificamos o valor de p:

Localizamos o foco e encontramos a equação da diretriz:

Finalmente,fazemos o gráfico usando os dados obtidos:
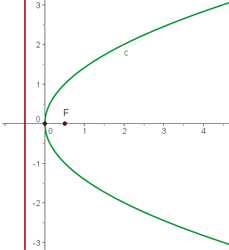
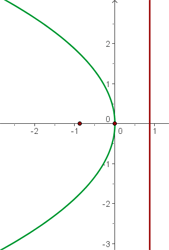
2. 
Isolamos o termo quadrático:

Identificamos o valor de p:

Localizamos o foco e encontramos a equação da diretriz:

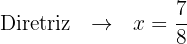
Finalmente, fazemos o gráfico usando os dados obtidos:
3. 
Isolamos o termo quadrático:

Identificamos o valor de p:

Localizamos o foco e encontramos a equação da diretriz:

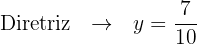
Finalmente, fazemos o gráfico usando os dados obtidos:
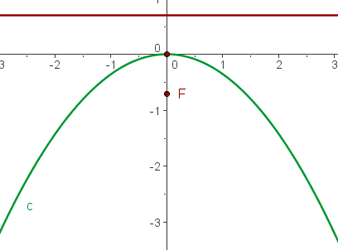
Calcule as coordenadas do vértice e do foco, e a equação da diretriz de cada parábola:



Novamente, vamos proceder determinando, na forma reduzida, as equações das parábolas, indicando o valor do parâmetro  , e com isso as coordenadas do foco e do vértice.
, e com isso as coordenadas do foco e do vértice.
1. 
Completamos o trinômio quadrado perfeito e isolamos:


Fatoramos:

Com a equação, identificamos seus elementos:
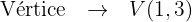
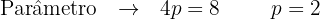
Com o vértice e o valor do parâmetro  , localizamos o foco e a diretriz:
, localizamos o foco e a diretriz:

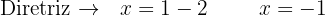
Finalmente, desenhamos o gráfico:
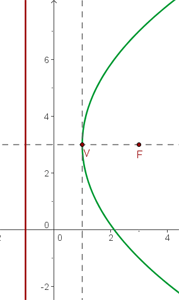
2. 
Completamos o trinômio quadrado perfeito e isolamos:

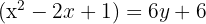
Fatoramos:

Com a equação, identificamos seus elementos:
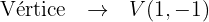
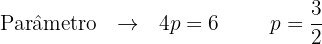
Com o vértice e o valor do parâmetro  , localizamos o foco e a diretriz:
, localizamos o foco e a diretriz:

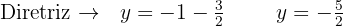
Finalmente, identificamos no gráfico:
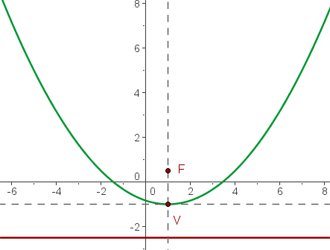
3. 
Completamos o trinômio quadrado perfeito e isolamos:


Fatoramos:
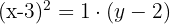
Com a equação, identificamos seus elementos:
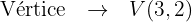
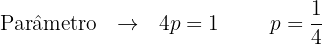
Com o vértice e o valor do parâmetro  , localizamos o foco e a diretriz:
, localizamos o foco e a diretriz:
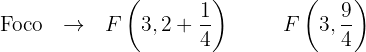
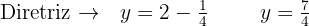
Finalmente, identificamos no gráfico:
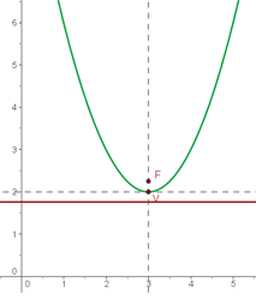
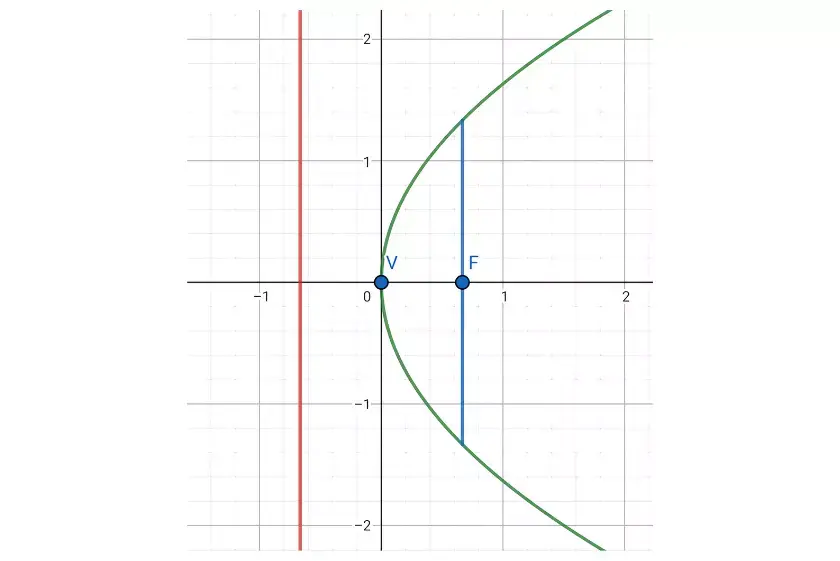
Encontre a equação da diretriz e o comprimento do lado reto da parábola 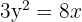 .
.
A equação da parábola pode ser expressa da seguinte forma:
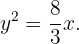
Disto, deduzimos que:
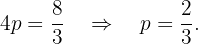
Portanto, o foco tem coordenadas  e a equação da diretriz é
e a equação da diretriz é 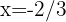 .
.
O lado reto) de uma parábola é a corda traçada pelo foco e paralela à sua diretriz. Para calcular seu comprimento, determinamos o valor de " " quando
" quando 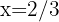 . Assim, se
. Assim, se 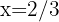 , então:
, então:

Aqui, consideramos o valor positivo, pois estamos calculando uma distância.
Assim, o comprimento do lado reto é o dobro dessa distância, ou seja,
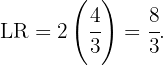
Determine a equação da parábola a partir de alguns de seus elementos
Determine as equações das parábolas que têm:
De diretriz  , de foco
, de foco 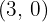 .
.
De diretriz 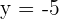 , de foco
, de foco  .
.
De diretriz  , de foco
, de foco 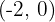 .
.
De diretriz  , de vértice
, de vértice  .
.
1. De diretriz  , de foco
, de foco 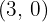 .
.
Ao localizar a diretriz e o foco, é fácil deduzir que a parábola tem abertura para a direita e seu vértice é na origem.

Sabendo que o foco para estas parábolas tem coordenadas 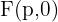 , concluimos que:
, concluimos que: 
Finalmente, a parábola tem uma equação:

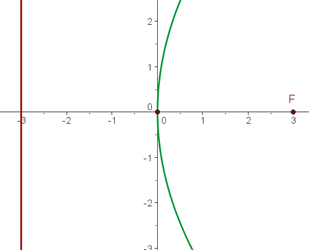
2. De diretriz 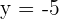 , de foco
, de foco  .
.
Ao localizar a diretriz e o foco, fica fácil deduzir que a parábola tem abertura para cima e seu vértice está na origem.
Sabendo que o foco para as parábolas dadas tem coordenadas 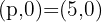 , concluimos que:
, concluimos que: 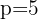 .
.
Substituimos na equação:


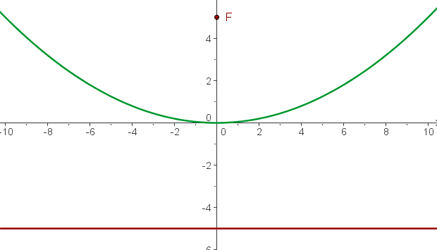
3. De diretriz  , de foco
, de foco 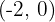 .
.
Ao localizar a diretriz e o foco, fica fácil deduzir que a parábola tem abertura para a esquerda e seu vértice é a origem.
O foco para parábolas que abrem para a esquerda tem coordenadas 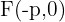 , isto significa que:
, isto significa que: 
Substituímos na equação:
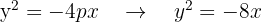
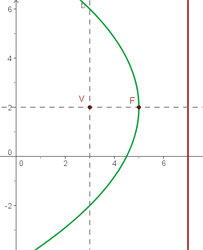
3. De diretriz  , de foco
, de foco 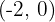 .
.
Ao localizar a diretriz e o foco, fica fácil deduzir que a parábola tem abertura em direção à esquerda e seu vértice está na origem.
O foco para parábolas que abrem para a esquerda tem como coordenadas 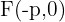 , e isso significa:
, e isso significa: 
Substituimos na equação:
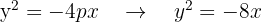
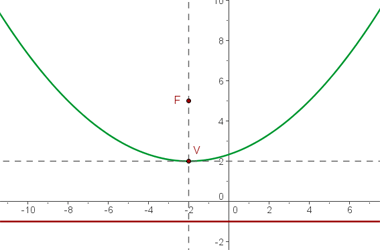
3. De diretriz  , de foco
, de foco 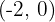
Ao localizar a direcriz e o foco, fica fácil deduzir que a parábola tem abertura para o lado esquerdo e o vértice está na origem.
O foco para parábolas que abrem para o lado esquerdo tem abertura para a esquerda, tem como coordenadas 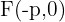 , ou seja,
, ou seja, 
Substituimos na equação:
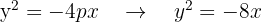
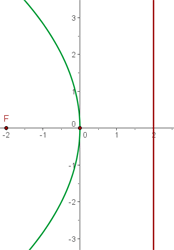
4. De diretriz  , de vértice
, de vértice  .
.
Ao localizar a diretriz e o vértice, fica fácil deduzir que a parábola tem abertura para baixo e seu vértice está na origem origen.
Para estas parábolas, a equação de diretriz é  . Sendo assim:
. Sendo assim: 
E a equação fica como segue:

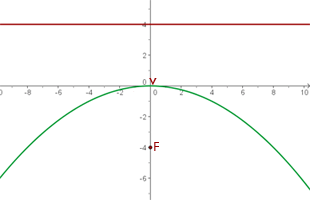
Determine as equações das parábolas considerando o foco e o vértice.
De foco  , de vértice
, de vértice  .
.
De foco 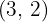 , de vértice
, de vértice 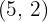 .
.
De foco 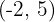 , de vértice
, de vértice  .
.
De foco  , de vértice
, de vértice 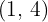 .
.
1. De foco  , de vértice
, de vértice  .
.
Ao localizar o foco e o vértice, fica fácil deduzir que a parábola abre em direção a direita e seu vértice está na origem. A equação tem a seguinte forma:

Lembrete que nestas parábolas, o foco está em 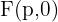 , sendo assim:
, sendo assim:

Finalmente, a equação da parábola tem a seguinte fórmula:

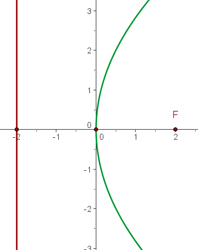
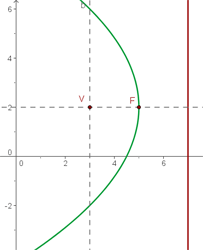
2. De foco (3, 2), de vértice (5, 2).
Situando o vértice e o foco, podemos notar que o foco está mais à esquerda do vértice, o que nos indica de que se trata de uma parabóla com abertura para o lado esquerdo e que tem a seguinte equação:
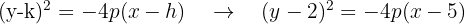
Calculamos a distância do vértice até o foco e vamos obter:

Substituimos na equação:
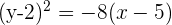
3. De foco (-2, 5), de vértice (-2, 2).
Ao posicionar o vértice e o foco, observamos que o foco está acima do vértice, o que indica que a parábola tem abertura para cima e sua equação segue a forma:
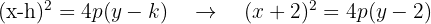
Calculamos a distância do vértice até o foco:

Substituimos na equação:

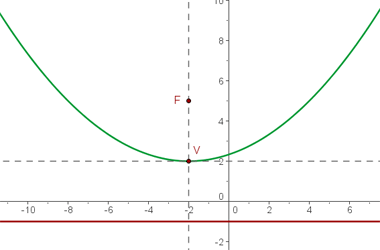
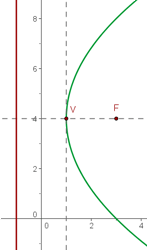
4. De foco (3, 4), de vértice (1, 4).
Marcando o vértice e o foco, podemos notar que o foco está a direita do vértice, o que indica que a parábola tem abertura para a direita:
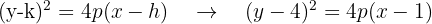
Calculamos a distância do vértice até o foco e obtemos:

Fazemos a substituição na equação:
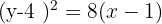
Determine a equação da parábola que têm como diretriz a reta:  e como foco, o ponto:
e como foco, o ponto:  .
.
Já sabemos que distância entre o vértice e o foco é igual a la distância entre o vértice e a diretriz.

A distância de uma reta  a um ponto
a um ponto  é dada por:
é dada por:
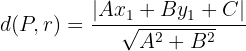
Dessa forma, se consideramos o vértice que desconhecemos como o ponto 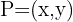 , a primeira equação é equivalente a:
, a primeira equação é equivalente a:
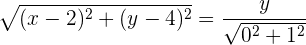
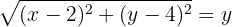
Elevamos ao quadrado para eliminar a raiz do lado esquerdo e desenvolvemos:


Isolamos, deixando as variáveis  de um lado, e
de um lado, e  do outro:
do outro:
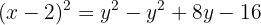
E, por fim, fatoramos:

Encontre uma equação para uma parábola que tem eixo horizontal, vértice em  e que passa pelo ponto
e que passa pelo ponto 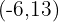
Dado que o eixo é horizontal e seu vértice está no ponto  , portanto, da equação:
, portanto, da equação:

obtemos a seguinte relação:
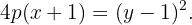
Se a parábola passa pelo ponto 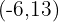 , então:
, então:

Dessa forma, vamos ter a equação:
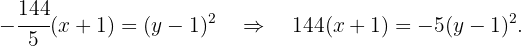
Simplificando a equação de cima, vamos obter a equação da parábola que queremos:

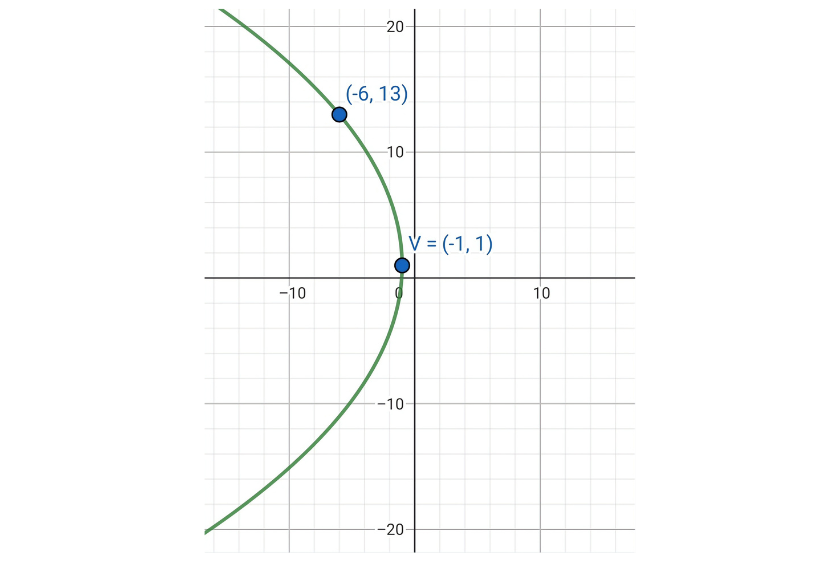
Parábola que passa por 3 pontos
Encontre a equação da parábola de eixo vertical e que passe pelos pontos:

A equação de uma parábola vertical tem como forma:
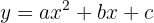
Como os pontos A, B e C passam pela parábola, suas coordenadas satisfazem sua equação.
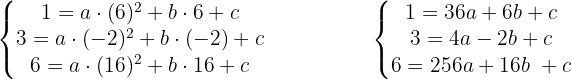
Resolvemos o sistema de equações e obtemos:
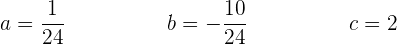
E, assim, a equação da parábola é:
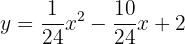
Posição relativa de reta e parábola
Determine a posição relativa da reta

em relação à parábola
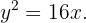
Para determinar a posição relativa entre os objetos, precisamos verificar a existência de pontos de interseção, cujas coordenadas devem satisfazer ambas as equações:
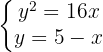
Para resolver el sistema, podemos elevar ao quadrado a segunda equação e igualar  das duas equações.
das duas equações.

Desenvolmemos:

Resolvemos a quadrática (fórmula geral):

Temos as coordenadas  , e para obter as coordenadas
, e para obter as coordenadas  , substituimos em uma das equações (escolhemos a mais simples):
, substituimos em uma das equações (escolhemos a mais simples):
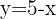
Assim:

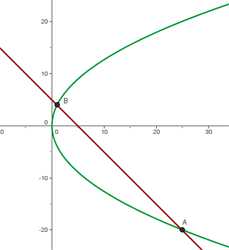
Os pntos de interseção são:

A reta é secante à parábola, pois há dois pontos de interseção, como ilustrado na imagem abaixo:
Determine a posição relativa da reta
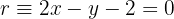
em relação à parábola
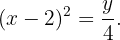
Para determinar a posição relativa entre os objetos, verificamos a existência de pontos de interseção, cujas coordenadas devem satisfazer ambas as equações:
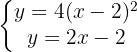 Para resolver o sistema, igualamos as duas equações e resolvemos para
Para resolver o sistema, igualamos as duas equações e resolvemos para 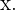

Resolvemos a equação quadrática usando a mesma fórmula geral que usamos no exercício anterior:

Temos as coordenadas  . Para obter as coordenadas
. Para obter as coordenadas  , substituimos em uma equação inicial. Escolhemos a segunda equação:
, substituimos em uma equação inicial. Escolhemos a segunda equação:
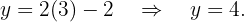
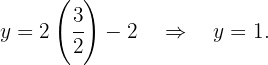
E, portanto, os pontos de interseção são:
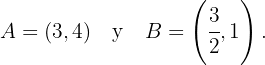
A reta é secante à parábola, pois intercepta-a em dois pontos distintos, conforme ilustrado na imagem.
Resumir com IA:












