Temas

Revisão
Observação: Todo número real é um número complexo, mas nem todo número complexo é um número real.
Fórmulas para operações com números complexos:
Adição
É feita somando as partes reais e as partes imaginárias em partes separadas:

Multiplicação
É feita como o produto de dois binômios, usando a propriedade distributiva,
lembrando que: 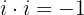
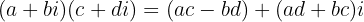
Divisão
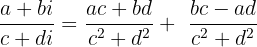
Aritmética de números complexos
Resolva o quociente dos números complexos a seguir:
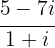
Aplicamos a fórmula de quociente de números complexos:
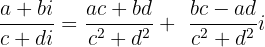
Dessa forma, vamos obter:
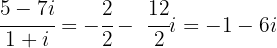
Resolva as seguintes operações:
1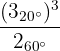
2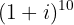
3
4
1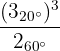
Primeiro elevamos o numerador à terceira potência

Calculamos o quociente
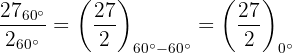
2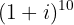
Convertemos o número 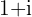 para forma polar
para forma polar
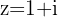
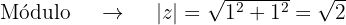

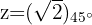
Calculamos a potência de 
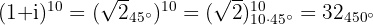
Ajustando o argumento entre o ângulo  e
e 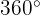 :
:

3
Convertemos  para forma polar
para forma polar

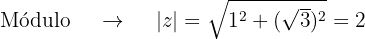
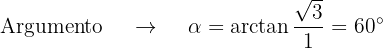

Calculamos a potência de 
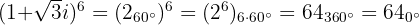
4
Convertemos o numerador para forma polar
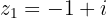
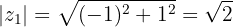
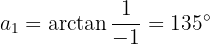

Convertemos o denominador para forma polar
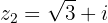
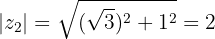
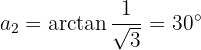

Calculamos o quociente
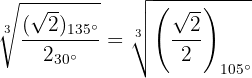
Obtemos o módulo e argumento das raízes
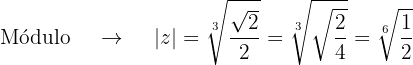
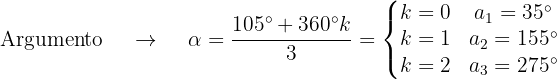
As raízes cúbicas são:
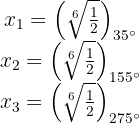
Resolva e expresse em forma polar
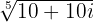
Convertemos o número 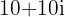 em forma polar
em forma polar

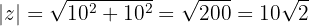
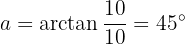
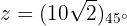
Então,
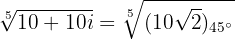
Para calcular as raízes, vamos calcular o módulo e os argumentos:
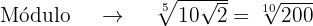
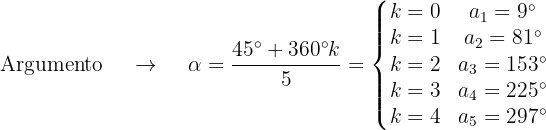
As 5 raízes quintas são representadas pelos seguintes números complexos:
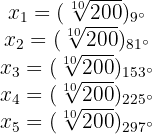
Calcule a operação abaixo, fornecendo o resultado em forma polar.
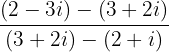
Removemos os parêntesis para realizar as operações com numerador e denominador:

Multiplicamos o numerador e o denominador pelo conjugado do denominador:
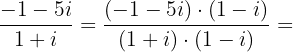
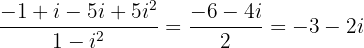
Então,

Para a forma polar, vamos calcular o módulo e o argumento:

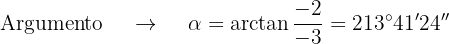
Sendo assim,
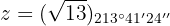
Calcule o valor do quociente. Calcule as raízes cúbicas, expressando em forma polar, trigonométrica e binomial
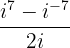
1 Cálculo do quociente
Trocamos o expoente negativos e desenvolvemos a operação:
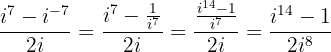
Considerando que 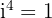 , obtemos:
, obtemos:
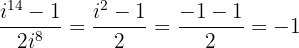
Portanto:
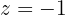
2 Conversão para forma polar
Para encontrar as raízes de  , convertemos para forma polar determinando módulo e argumento:
, convertemos para forma polar determinando módulo e argumento:
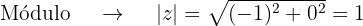

Logo:

3 Cálculo das raízes cúbicas
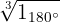
Determinamos módulo e argumento das raízes:

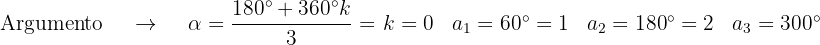
As 3 raízes cúbicas são:
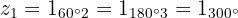
4 Raízes em forma trigonométrica e binomial
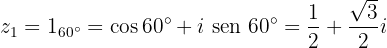
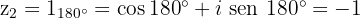
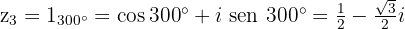
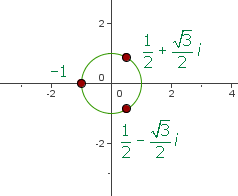
Raízes de uma equação
Calcule as raízes da seguinte equação:



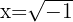
Trocamos a forma polar do número dentro da raiz, neste caso, -1.
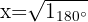
Determinamos o módulo e o argumento das raízes:
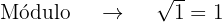
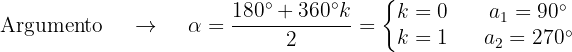
As raízes da equação são, então, os números de módulo 1 e com os argumentos mencionados anteriormente, ou seja,
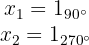
Calcule as raízes da equação a seguir:


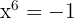
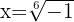
Trocamos a forma polar do número dentro da raiz, neste caso, -1.
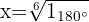
Determinamos o módulo e o argumento das raízes:
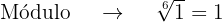
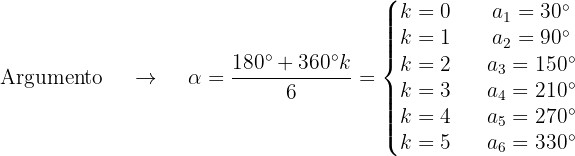
As raízes da equação são, então, os números de módulo 1 e com os argumentos mencionados anteriormente, ou seja,
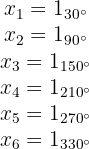
Calcule todas as raízes da equação:
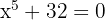
Isolamos:
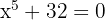

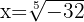
Trocamos a forma polar do número dentro da raiz:
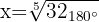
Determinamos o módulo e o argumento das raízes:

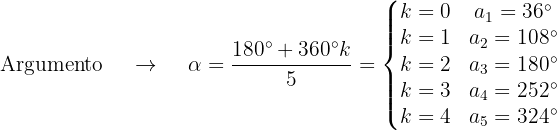
As raízes quintas são, então, os números:
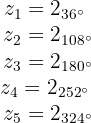
Escreva uma equação de segundo grau que tenha como solução  e o número conjugado.
e o número conjugado.
Considerando um número complexo conjugado:
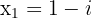
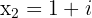
Podemos encontrar uma equação de segundo grau em que as soluções sejam os números. A equação pode ser escrita assim:
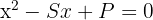
Onde  é a soma das raízes e
é a soma das raízes e  é o produto. Neste caso,
é o produto. Neste caso,
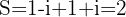
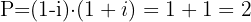
Portanto, a equação que estamos procurando é:
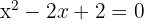
Escreva uma equação de segundo grau que tenha como soluções 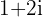 e número complexo conjugado.
e número complexo conjugado.
Considerando um número complexo conjugado
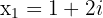

Podemos encontrar uma equação de segundo grau que os resultados sejam os números determinados. A equação é escrita da seguinte forma:
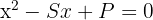
Onde  é a soma das raízes e
é a soma das raízes e  é o produto. Neste caso,
é o produto. Neste caso,
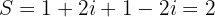
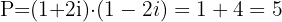
Portanto, a equação que estamos buscando é:

Conjugado de um número complexo, forma polar e trigonométrica
Determine o resultado da soma de um número com seu conjugado.
Vamos considerar o número complexo 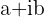 e o conjugado
e o conjugado 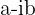
Fazemos a adição:
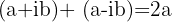
Dessa forma, a soma de um número complexo com seu conjugado é igual ao dobro da parte real do número complexo.
Determina o resultado da multiplicação de número complexo com o conjugado
Vamos considerar este número complexo 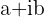 e este conjugado
e este conjugado 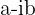
Vamos fazer a multiplicação:
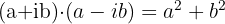
Dessa forma, o produto de um número complexo comov conjugado é igual à soma dos quadrados da parte real e da parte imaginária do número complexo.
Determine o resultado da diferença entre um número complexo e o conjugado.
Vamos levar em consideração o número complexo 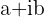 e o conjugado
e o conjugado 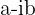
Realizamos a subtração:
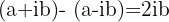
Assim, a diferença de um número complexo com seu conjugado é igual ao dobro da parte imaginária do número complexo.
Defina as formas polar e trigonométrica, os conjugados e os opostos de:
a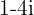
b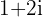
a 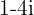
Primeiro, vamos obter o módulo e o argumento das raízes:
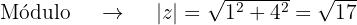
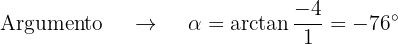
Dessa forma,  a forma polar e trigonométrica fica assim:
a forma polar e trigonométrica fica assim:
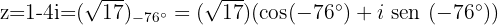
O conjugado:
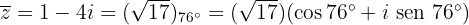
O oposto:
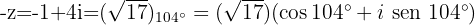
b 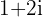
Como no exemplo anterior, primeiro, obtemos o módulo e o argumento das raízes:
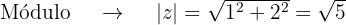
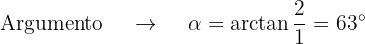
Então,  a forma polar e trigonométrica fica:
a forma polar e trigonométrica fica:
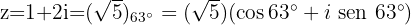
O conjugado:
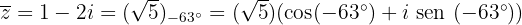
O oposto:
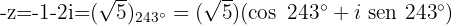
Determine as formas polar e trigonométrica, os conjugados e os opostos de:
a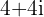
b
a 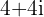
Obtemos o módulo e o argumento das raízes:
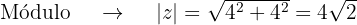
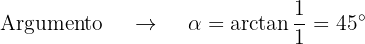
Portanto,  na forma polar e trigonométrica fica desse jeito:
na forma polar e trigonométrica fica desse jeito:
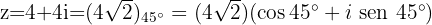
O conjugado:
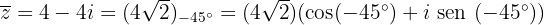
O oposto:
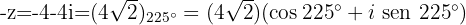
b 
Obtemos o módulo e o argumento das raízes:
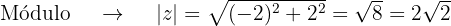
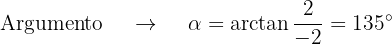
Então,  a forma polar e trigonométrica é:
a forma polar e trigonométrica é:

O conjugado:

O oposto:
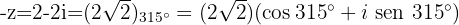
Teorema de Moivre e binômio de Newton
Expresa en forma polar y binómica un complejo cuyo cuadrado sea:
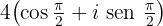
Convertimos a forma polar
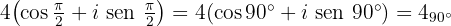
Queremos encontrar un número  , tal que al elevarlo al cuadrado resulte el número anterior
, tal que al elevarlo al cuadrado resulte el número anterior
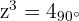
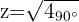
Obtenemos el módulo y el argumento de las raíces

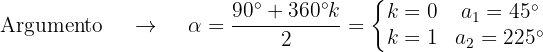
Las 3 raíces cuadradas constan entonces de los números
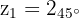
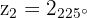
Eso convertido a forma trigonométrica y binomial obtengo
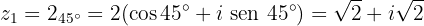
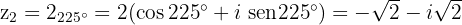
Expresse na forma polar e algébrica um número complexo cujo cubo seja:
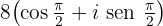
Convertendo para a forma polar:
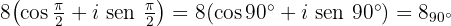
Queremos encontrar um número  , que, ao elevá-lo ao cubo, resulte no número acima:
, que, ao elevá-lo ao cubo, resulte no número acima:

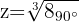
Calculamos o módulo e o argumento das raízes:

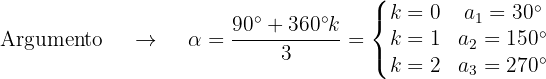
Então, as três raízes cúbicas são:

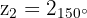
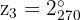
Convertendo para a forma trigonométrica e algébrica, obtemos:

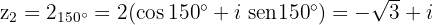
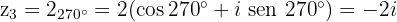
Determine a função de cos α e sen α:
a 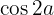
b 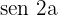
1 Binômio de Newton:
Aplicamos o binômio de Newton:
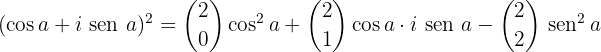
Desenvolvemos:
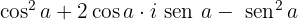
Separamos a parte real e a parte imaginária:
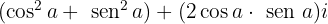
2 Fórmula de Moivre:
Por outro lado, sabemos que:
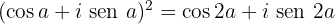
Usando o resultado que obtivemos com o binômio de Newton, igualamos as partes reais e concluímos que:
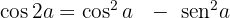
Igualando as partes imaginárias, concluímos que:
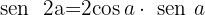
Determine a função de cos α y sen α:
a 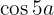
b 
1 Binomio de Newton:
Aplicamos o binômio de Newton:
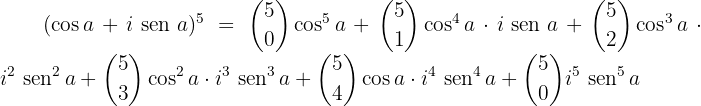
Desenvolvemos:
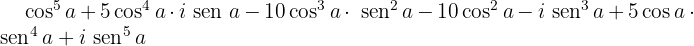
Separamos a parte real e a parte imaginária:
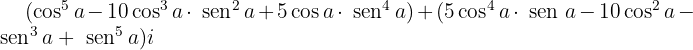
2 Fórmula de Moivre:
Por outro lado, sabemos que:

Usando o resultado que obtivemos com o binômio de Newton, igualamos as partes reais e concluímos que:

Igualando as partes imaginárias, concluímos que:
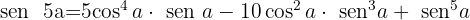
Defina a função de 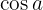 y
y  :
:
a 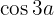
b 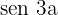
1 Binomio de Newton:
Aplicamos o binômio de Newton:

Desenvolvemos:
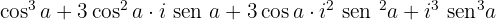
Separamos a parte real e a parte imaginária:
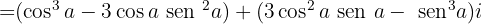
2 Fórmula de Moivre:
Por outro lado, sabemos que:

Usando o resultado que obtivemos com o binômio de Newton, igualamos as partes reais e concluímos que:

Igualando as partes imaginárias, concluímos que:
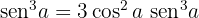
Resumir com IA:












