Temas

Demonstre as identidades trigonométricas


Usamos a definição de tangente e cotangente para desenvolver o lado esquerdo da equação

Usamos que  e as definições de secante e cossecante para obter:
e as definições de secante e cossecante para obter:

que é o que queríamos demonstrar.


Primeiro desenvolvemos o quadrado:

Fatoramos  dos dois termos, usamos a identidade
dos dois termos, usamos a identidade  e a definição de cossecante e cotangente.
e a definição de cossecante e cotangente.



Desenvolvemos o lado direito, começando por fatorar  de ambos os termos:
de ambos os termos:

Usamos a identidade  e a definição de secante
e a definição de secante

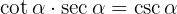
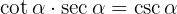
Usamos a definição de cotangente e secante
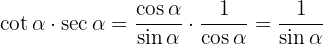
Cancelamos o fator 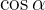 e usamos a definição de cossecante
e usamos a definição de cossecante
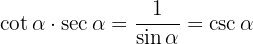
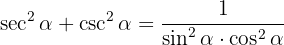
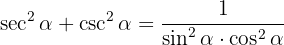
Desenvolvemos com as definições de secante e cossecante e fazemos a soma das frações
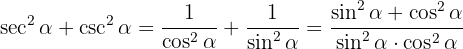
Finalmente, usamos a identidade  e obtemos o resultado que queríamos demonstrar:
e obtemos o resultado que queríamos demonstrar:
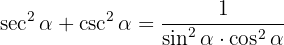
Demonstre as identidades com fórmulas de adição
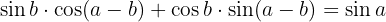
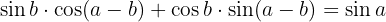
Primeiro, notamos que:
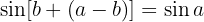
A fórmula da soma do seno é:
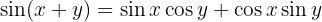
E, ao usá-la, obtemos a identidade desejada de forma imediata:
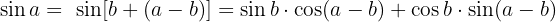
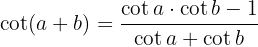
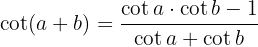
A definição de cotangente diz que:

Usamos a fórmula da soma da tangente e simplificamos:

Dividimos numerador e denominador por
 , para depois usar a definição de cotangente e simplificar a expressão:
, para depois usar a definição de cotangente e simplificar a expressão:
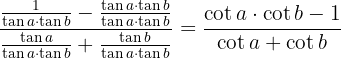
Simplifique as frações
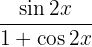
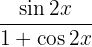
Usamos a fórmula do seno do ângulo duplo:

Consideramos que, como  então,
então, 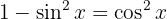
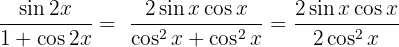
Simplificamos e aplicamos a definição de tangente:
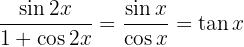
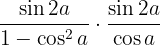
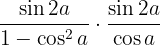
Substituímos com  e usamos a fórmula do seno do ângulo duplo, depois realizamos a multiplicação das frações:
e usamos a fórmula do seno do ângulo duplo, depois realizamos a multiplicação das frações:
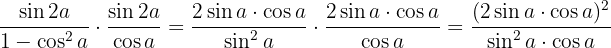
Desenvolvemos e simplificamos:
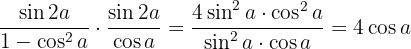
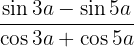
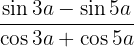
Usamos as fórmulas para transformar somas em produtos de funções trigonométricas:

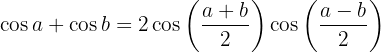
Portanto,
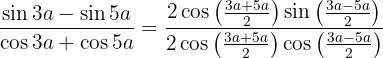
Simplificamos e usamos a definição da tangente. Além disso, a tangente é uma função ímpar, ou seja, 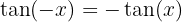
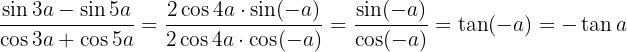
Resumir com IA:












