Temas
Uma equação de segundo grau é toda expressão com a forma:
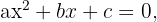 onde
onde 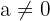

Resolução de equação de 2º grau
Uma equação de 2º grau é resolvida aplicando a seguinte fórmula:
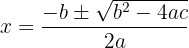
Exemplo: Encontre as soluções de 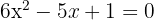
1. Primeiro encontramos os valores dos coeficientes:
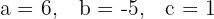
2. Substituímos os valores na fórmula e resolvemos:

3. Vamos obter dois valores para  , que são normalmente representados por
, que são normalmente representados por  :
:
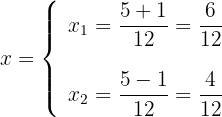
4. Simplificamos os resultados e obtemos:
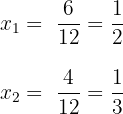
Discriminante e tipos de soluções
O radicando da raiz quadrada presente na fórmula utilizada para resolver uma equação do segundo grau é conhecido como discriminante.
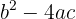
A partir do discriminante é possível estabelecer o tipo de soluções da equação de segundo grau.
1. Se 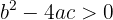 , então
, então 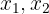 são soluções reais e diferentes.
são soluções reais e diferentes.
2. Se 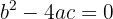 , então
, então 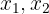 são soluções reais e iguais.
são soluções reais e iguais.
3. Se 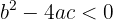 , então a equação não possui soluções reais.
, então a equação não possui soluções reais.
Exemplo: Determine os tipos de soluções de 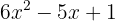
Os coeficientes são 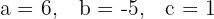
Substituímos os valores na fórmula e resolvemos:
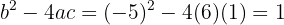
Como o discriminante é maior que zero, a equação do segundo grau tem duas soluções reais e diferentes.
Exercícios de equações do 2º grau a partir de suas soluções
Encontre as equações do segundo grau que têm como soluções:

a. Como conhecemos as raízes  da equação de segundo grau, podemos escrevê-la dessa forma:
da equação de segundo grau, podemos escrevê-la dessa forma:

b. Substituímos as raízes e obtemos:
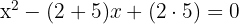
c. Assim, a equação buscada é:
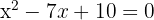

a. Se já conhecemos as raízes  da equação de segundo grau, podemos escrevê-la dessa forma:
da equação de segundo grau, podemos escrevê-la dessa forma:

b. Substituímos as raízes e obtemos:

c. Assim, a equação que procuramos é:

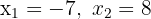
a. Como já conhecemos as raízes 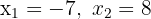 da equação de segundo grau, vamos escrevê-la assim:
da equação de segundo grau, vamos escrevê-la assim:

b. Substituímos as raízes e vamos obter:

c. Dessa forma, a equação que estamos procurando é:

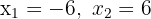
a. Se conhecemos as raízes 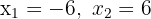 da equação de segundo grau, podemos escrevê-la como:
da equação de segundo grau, podemos escrevê-la como:

b. Agora, vamos substituir as raízes e obtemos:
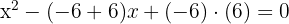
c. Assim, a equação que queremos é:


a. Como já conhecemos as raízes  da equação de segundo grau, vamos escrever assim:
da equação de segundo grau, vamos escrever assim:

b. Fazemos a substituição das raízes e vamos obter:
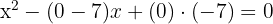
c. Dessa forma, encontramos essa equação:

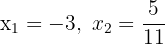
a. Já conhecemos as raízes 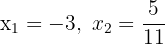 da equação de segundo grau, vamos escrevê-la assim:
da equação de segundo grau, vamos escrevê-la assim:

b. Substituímos as raízes e encontramos:
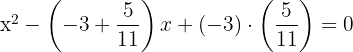
c. Portanto, a equação será:

d. A equação anterior pode ser expressa com coeficientes inteiros; para isso, multiplicamos os dois lados da equação por  :
:

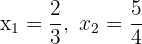
a. Como conhecemos as raízes 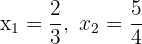 da equação de segundo grau, podemos escrevê-la dessa maneira:
da equação de segundo grau, podemos escrevê-la dessa maneira:

b. Vamos substituir as raizes e assim obter:
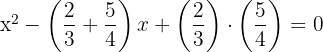
c. Portanto, a equação procurada é:

d. A equação anterior pode ser expressa com coeficientes inteiros; para isso, multiplicamos os dois lados da equação por  :
:
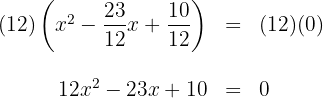
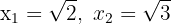
a. Conhecendo as raízes 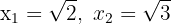 da equação de segundo grau, podemos escrevê-la assim:
da equação de segundo grau, podemos escrevê-la assim:

b. Substituímos as raízes e obtemos:
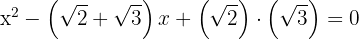
c. Assim, a equação que procuramos é:
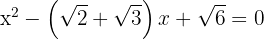
Exercícios de fatoração de equações de 2º grau
Faça a fatoração das equações de segundo grau abaixo:
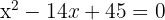
a. Os coeficientes da equação de segundo grau são:  .
.
b. Substituímos os valores na fórmula para encontrar as soluções e resolvemos:
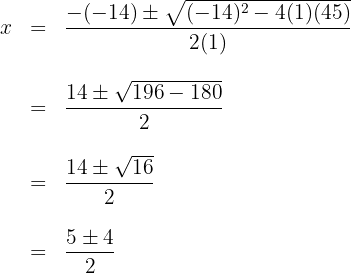
c. Observamos que são obtidos dois valores para  , que geralmente são representados
, que geralmente são representados  :
:
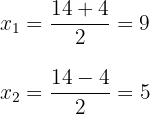
d. A fatoração procurada é dada por: 
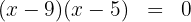
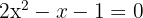
a. Os coeficientes da equação de segundo grau são: 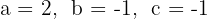 .
.
b. Substituímos os valores na fórmula para encontrar as soluções e resolvemos:
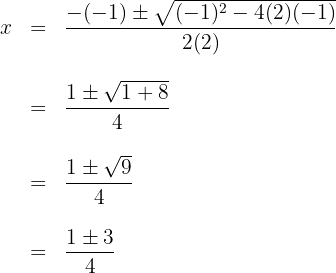
c. Observamos que são obtidos dois valores para  , que normalmente são representados
, que normalmente são representados 
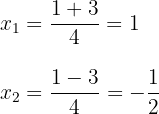
d. A fatoração procurada é dada por: 
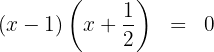
e. Podemos obter os fatores com coeficientes inteiros; para isso, escrevemos o segundo fator com um denominador comum e depois multiplicamos os dois lados da equação por esse denominador:
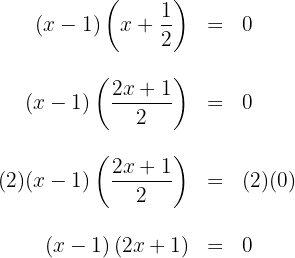
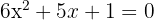
a. Os coeficientes da equação de segundo grau são: 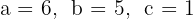 .
.
b. Substituímos os valores na fórmula para encontrar as soluções e resolvemos:
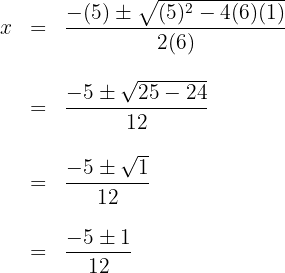
c. Observamos que são obtidos dois valores para  , que geralmente são representados por:
, que geralmente são representados por: 
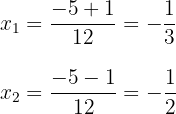
d. A fatoração procurada é dada por: 

e. Podemos obter os fatores com coeficientes inteiros; para isso, escrevemos cada fator com um denominador comum e depois multiplicamos os dois lados da equação pelo produto desses denominadores:
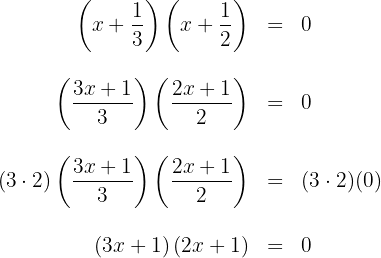

a. Os coeficientes da equação de segundo grau são: 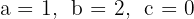 .
.
b. Substituímos os valores na fórmula para encontrar as soluções e resolvemos:

c. Observamos que são obtidos dois valores para  , que normalmente são representados por:
, que normalmente são representados por: 
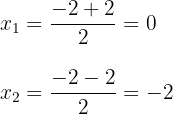
d. A fatoração procurada é dada por: 
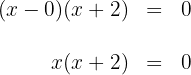
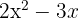
a. Os coeficientes da equação de segundo grau são: 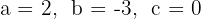 .
.
b. Substituímos os valores na fórmula para encontrar as soluções e resolvemos:

c. Observamos que são obtidos dois valores para  , que geralmente são representados por:
, que geralmente são representados por: 

d. A fatoração procurada é dada por: 
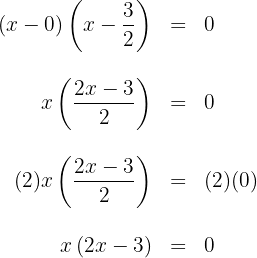
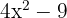
a. Os coeficientes da equação de segundo grau são: 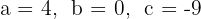 .
.
b. Substituímos os valores na fórmula para encontrar as soluções e resolvemos:
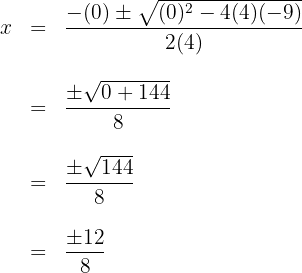
c. Observamos que são obtidos dois valores para  , que geralmente são representados por:
, que geralmente são representados por: 
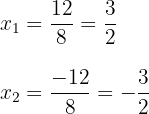
d. A fatoração procurada é dada por: 
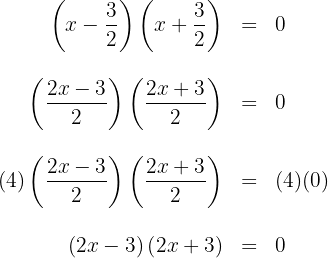
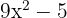
a. Os coeficientes da equação de segundo grau são: 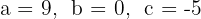 .
.
b. Substituímos os valores na fórmula para encontrar as soluções e resolvemos:
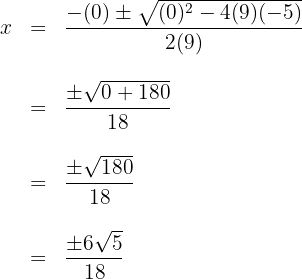
c. Observamos que são obtidos dois valores para  , que geralmente são representados por:
, que geralmente são representados por: 
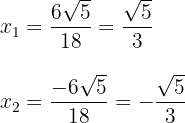
d. A fatoração procurada é dada por: 

Resumir com IA:












