Temas
Na estatística, os quartis são valores que dividem um conjunto de dados ordenados em quatro partes iguais, permitindo analisar a distribuição dos dados de forma mais detalhada. Os quartis fornecem uma medida importante de dispersão e são fundamentais para descrever a variabilidade dentro de um conjunto de dados.
Neste conjunto de exercícios resolvidos, veremos passo a passo como calcular e analisar os quartis de um conjunto de dados, com exemplos práticos que ilustram tanto os métodos de cálculo quanto sua interpretação em contextos estatísticos. Esses exercícios ajudam a fortalecer a compreensão das técnicas de análise de dados e a desenvolver habilidades essenciais para interpretar a distribuição e a dispersão dos valores.

Cálculo de quartil de um conjunto de dados
Calcule os quartis do conjunto: 
Vamos começar colocando em ordem crescente, de modo que seja obtido 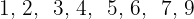 .
.
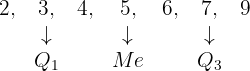
Calcule os quartis do conjunto: 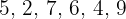
Vamos colocar o conjunto em ordem crescente, de modo que seja obtido 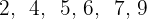 .
.
Neste caso: 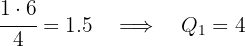
Neste caso: 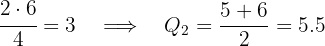
Neste caso: 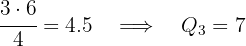
Calcule os quartis do conjunto: 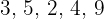
Vamos colocar o conjunto em ordem crescente, de modo que seja obtido 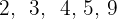 .
.
Neste caso: 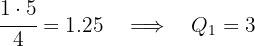
Neste caso: 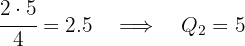
Neste caso: 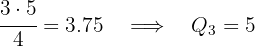
Calcule os quartis do conjunto: 
Vamos colocar o conjunto em ordem crescente, de modo que seja obtido 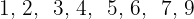
Neste caso: 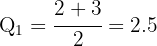
Neste caso: 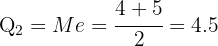
Neste caso: 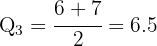
Calcule os quartis do conjunto: 
Ordenamos o conjunto 
Neste caso: 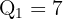
Neste caso: 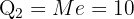
Neste caso: 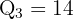
Cálculo de quartil utilizando diferentes tabelas
Calcule o quartil  da tabela a seguir:
da tabela a seguir:
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
Determinamos a posição em que se encontra o primeiro quartil:
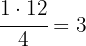
Assim, o primeiro quartil é:
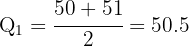
Calcule o quartil  da tabela a seguir:
da tabela a seguir:
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
Determinamos a posição em que se encontra o terceiro quartil:
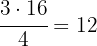
Dessa forma, o terceiro quartil é:
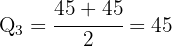
Calcule o quartil  da tabela abaixo:
da tabela abaixo:
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
Determinamos a posição em que se encontra o segundo quartil:
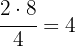
Assim, o segundo quartil é:
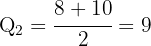
Calcule os quartis  e
e  da tabela:
da tabela:
 | |
 |  |
 |  |
 |  |
 |  |
 |  |
Identificamos o intervalo em que se encontra o primeiro quartil, multiplicando 1 por e dividido por
e dividido por 
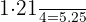
Procuramos na coluna das frequências acumuladas  intervalo que contém
intervalo que contém 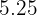
A classe de 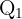 é:
é: 
Aplicamos a fórmula para o cálculo dos quartis em dados agrupados, obtendo:


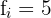

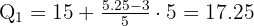
Cálculo do terceiro quartil
Identificamos o intervalo em que se encontra o terceiro quartil, multiplicando  por
por  e dividido por
e dividido por 

Procuramos na coluna das frequências acumuladas  o intervalo que contém
o intervalo que contém 
A classe de 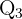 é:
é: 
Aplicamos a fórmula para o cálculo dos quartis em dados agrupados, obtendo:

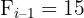



Dada a distribuição estatística:
 | |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
Calcule os quartis  e
e  .
.
Ampliamos a tabela com mais uma coluna, onde indicamos a frequência acumulada  :
:
Na primeira linha colocamos a primeira frequência absoluta. Na segunda, somamos o valor da frequência acumulada anterior com a frequência absoluta correspondente, e assim sucessivamente até a última linha, que deve ser igual a  , conforme mostrado a seguir:
, conforme mostrado a seguir:
 , conforme abaixo:
, conforme abaixo:
 |  |  | |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  | |
 |
Cálculo do primeiro quartil
Identificamos o intervalo em que se encontra o primeiro quartil, multiplicando 1 por  e dividindo por
e dividindo por 
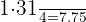
Procuramos na coluna das frequências acumuladas  o intervalo que contém
o intervalo que contém 
A classe de 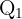 é: [5, 10)
é: [5, 10)
Aplicamos a fórmula para o cálculo dos quartis em dados agrupados, obtendo:


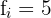

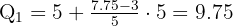
Cálculo do terceiro quartil
Identificamos o intervalo em que se encontra o terceiro quartil, multiplicando  por
por  e dividindo por
e dividindo por 
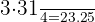
Procuramos na coluna das frequências acumuladas  o intervalo que contém
o intervalo que contém 
A classe de 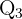 é:
é: 
Aplicamos a fórmula para o cálculo dos quartis em dados agrupados, obtendo:


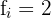


Problema de distribuição estatística
O número de dias que os alunos de uma escola faltaram devido a diversas doenças está representado na tabela a seguir:
 | |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
A partir de qual valor se encontra 25% do número de alunos com a maior quantidade de faltas?
Cálculo do terceiro quartil
Determinamos a posição em que se encontra o terceiro quartil, multiplicando 3 por 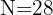 e dividindo por
e dividindo por 
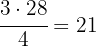
Procuramos na coluna das frequências absolutas a posição 
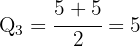
O número de dias que uma empresa de entregas demora para entregar 16 produtos está representado na tabela a seguir:
 | |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
A partir de qual valor se encontra 25% das entregas mais demoradas?
Cálculo do terceiro quartil
Determinamos a posição em que se encontra o terceiro quartil, multiplicando 3 por 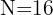 e dividindo por
e dividindo por 
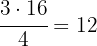
Procuramos na coluna das frequências absolutas a posição  .
.
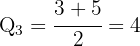
A seguir, estão as alturas de um grupo de alunos de um colégio:
 | |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
A partir de qual valor se encontra 25% das maiores alturas?
Cálculo do terceiro quartil
Determinamos a posição em que se encontra o terceiro quartil, multiplicando 3 por 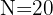 e dividindo por
e dividindo por 
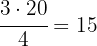
Procuramos na coluna das frequências absolutas a posição  .
.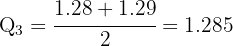
A seguir, são apresentadas as temperaturas registradas em uma determinada população ao longo de um ano.
 | |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
Até que valor se encontra 25% das temperaturas mais baixas?
Ampliamos a tabela com outra coluna, onde indicamos a frequência acumulada  :
:
Na primeira linha colocamos a primeira frequência absoluta. Na segunda linha somamos o valor da frequência acumulada anterior à frequência absoluta correspondente e assim sucessivamente até a última, que deve ser igual a  , de la seguinte maneira:
, de la seguinte maneira:
 |  |  | |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  | |
 |
Cálculo do primeiro quartil
Identificamos o intervalo em que se encontra o primeiro quartil, multiplicando 1 por  e dividindo por
e dividindo por 
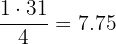
Procuramos na coluna das frequências acumuladas  o intervalo que contém
o intervalo que contém 
A classe de 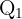 é: [5, 10)
é: [5, 10)
Aplicaremos a fórmula para o cálculo de quartil para dados agrupados, extraindo os seguintes dados:


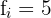

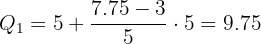
O histograma da distribuição correspondente ao peso de  alunos do Ensino Médio é o seguinte:
alunos do Ensino Médio é o seguinte:
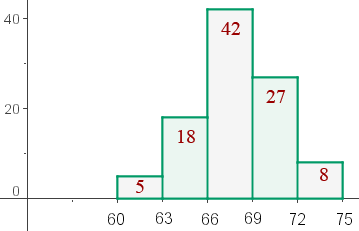
A partir de quais valores se encontram os dos alunos mais pesados?
Construímos a tabela:
 |  |  | |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |
Cálculo do terceiro quartil
Identificamos o intervalo em que se encontra o terceiro quartil, multiplicando  por
por  e dividindo por
e dividindo por  .
.
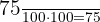
Procuramos na coluna das frequências acumuladas  o intervalo que contém
o intervalo que contém  .
.
A classe de 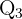 é:
é:  .
.
Aplicamos a fórmula para o cálculo do quartil em dados agrupados, obtendo os seguintes valores:
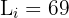
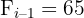
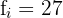
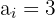
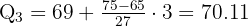
Resumir com IA:












