Bem-vindos à nossa seção dedicada ao cálculo de volumes associados a funções, utilizando o cálculo integral. Esse tema é fundamental tanto na matemática quanto na física e compreender esse conteúdo é essencial para resolver diversos problemas que envolvem áreas e volumes no espaço tridimensional. Aqui, vamos te acompanhar passo a passo no processo de determinação de volumes por meio de técnicas integrais.
O processo de calcular o volume gerado por uma função significa imaginar um sólido tridimensional sendo dividido em elementos infinitamente pequenos e, em seguida, somar esses elementos por meio de integrais definidas para obter o volume total. Esse método permite compreender, representar e quantificar a extensão de objetos no espaço tridimensional com precisão.
Vamos aplicar esses conceitos na prática!
Determine o volume do tronco de cone gerado pela rotação em torno de 
da área limitada por 
.
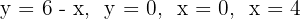1. Representamos graficamente o problema:
2. Substituímos na fórmula para encontrar o volume:
3. Para resolver a integral, consideramos a substituição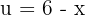 
e calculamos a derivada:
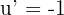
4. Aplicamos a fórmula geral de integração:
5. Como se trata de uma integral definida, descartamos a constante de integração:
6. Avaliamos nos extremos de integração:
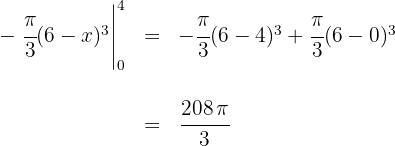
Logo, o volume é: 
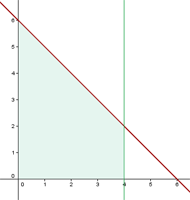
Calcule o volume gerado pelas superfícies limitadas pela curva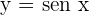 
e pelas retas 
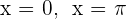, ao girar em torno do eixo OX .
1. Representamos graficamente o problema:
2.Substituímos na fórmula para encontrar o volume:
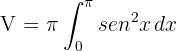
3. Para resolver a integral, consideramos a identidade trigonométrica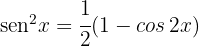 
, de modo que a integral é escrita como:
4. Por se tratar de uma integral definida, podemos dispensar a constante de integração:
5. Avaliamos nos extremos de integração
Portanto, o volume é:
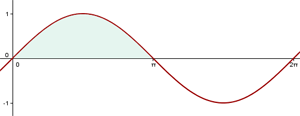
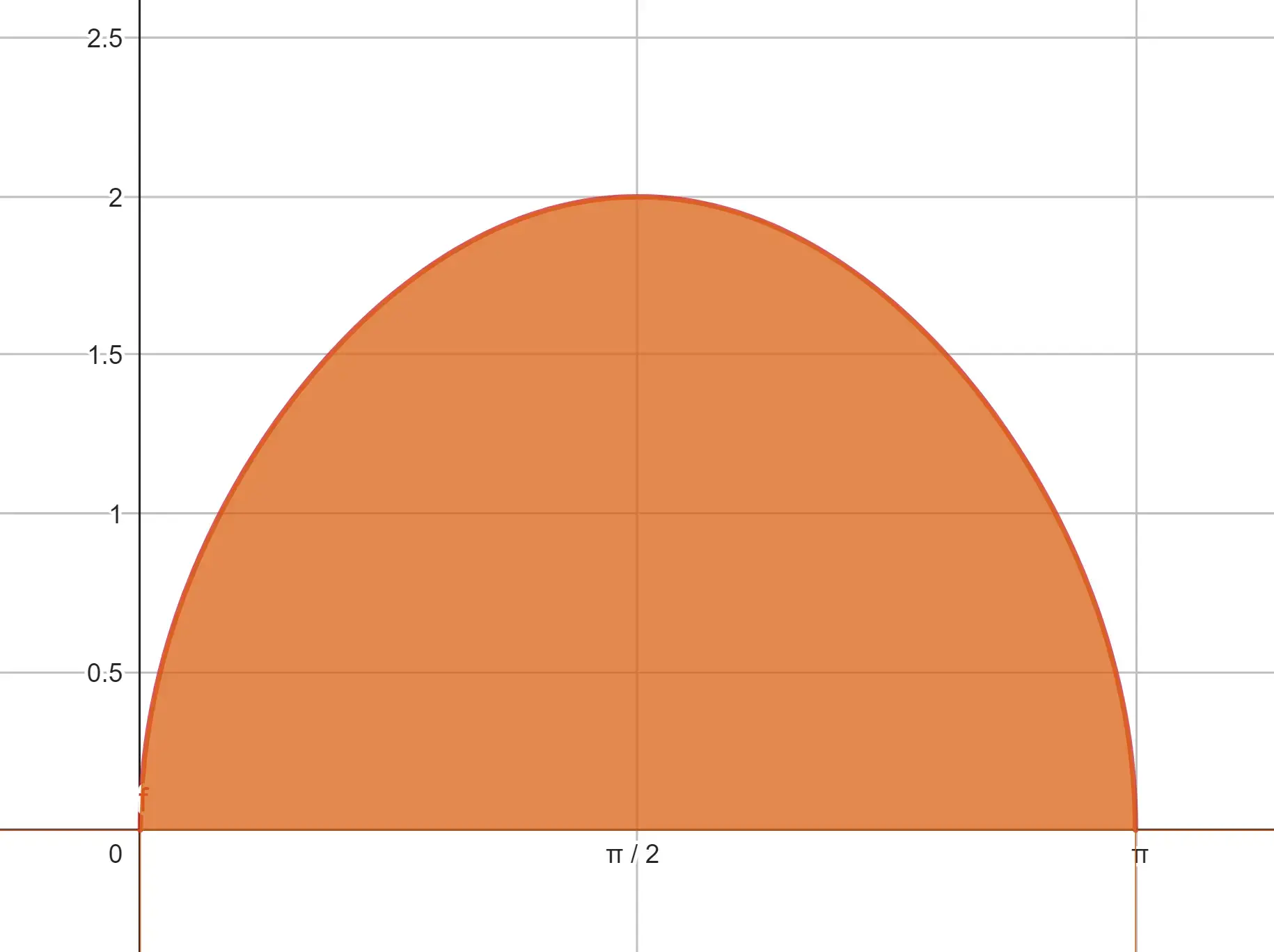
Calcule o volume gerado por uma semi-onda da função senoidal 
, ao girar em torno do eixo .
1. Representamos graficamente o problema:
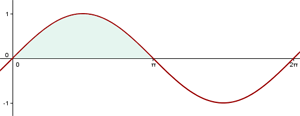
Observamos que a função senoidal corresponde à mesma curva utilizada na figura do exercício 2.
2. Substituímos na fórmula para encontrar o volume
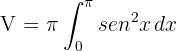
3. Para resolver a integral, utilizamos a identidade trigonométrica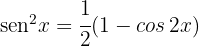, de modo que a integral pode ser escrita como:
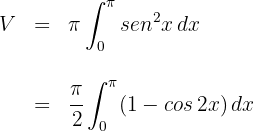
4. Como se trata de uma integral definida, podemos dispensar a constante de integração:
5. Avaliamos nos extremos de integração
Portanto, volume é:
Calcule o volume do corpo de revolução gerado ao girar em torno do eixo , a região determinada pela função 
,pelo eixo das abscissas e pelas retas .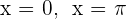
1. Substituímos na fórmula para encontrar o volume
2. Desenvolvemos o integrando
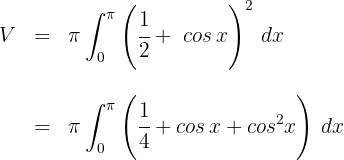
3. Consideramos a identidade trigonométrica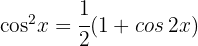 
. Como se trata de uma integral definida, podemos dispensar a constante de integração:
4. Avaliamos nos extremos de integração
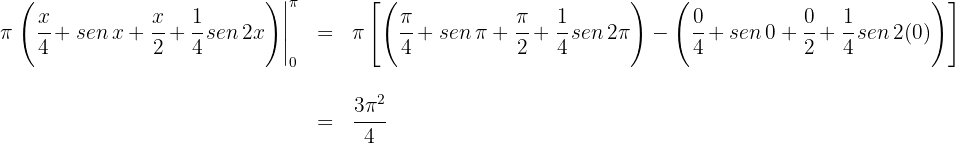
Logo, o volume é
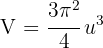
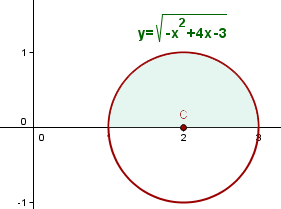
Calcule o volume gerado pelo círculo 
ao girar em torno do eixo .
1. Escrevemos a equação do círculo em sua forma ordinária:
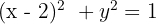
2. O centro da circunferência é 
e o raio é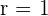 
. Os pontos de interseção com o eixo são:
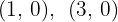
3. A partir da equação geral do círculo, obtemos a função:
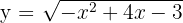
4. Substituímos na fórmula para encontrar o volume:
5. Desenvolvemos o integrando:
6. Como se trata de uma integral definida, podemos dispensar a constante de integração:
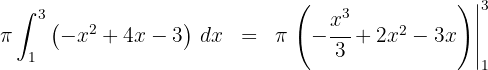
7. Avaliamos nos extremos de integração:
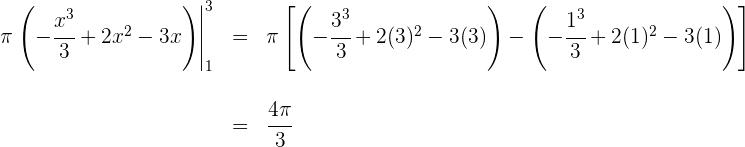
Portanto, o volume é
Calcule o volume gerado ao girar, em torno do eixo ,a área limitada pelos gráficos de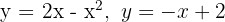 
.
1. Para encontrar os pontos de interseção entre a reta e a parábola, resolvemos o sistema:
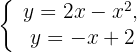
Igualamos as expressões e efetuamos a fatoração para determinar:
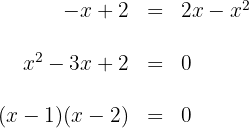
As raízes são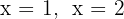 
. Assim, os pontos de interseção são: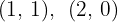 
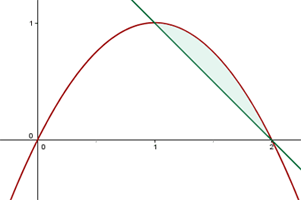
2.Substituímos na fórmula para encontrar o volume
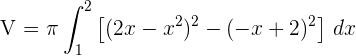
3.Desenvolvemos o integrando
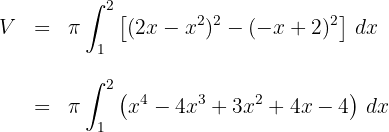
4. Como se trata de uma integral definida, podemos dispensar a constante de integração
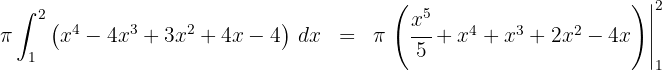
5. Avaliamos nos extremos de integração
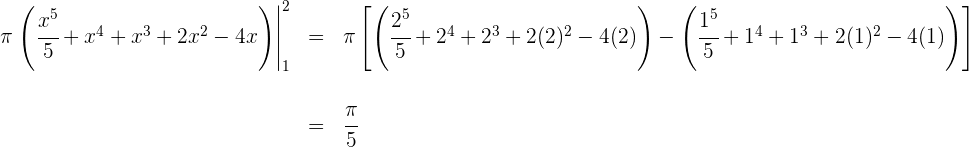
Assim, o volume é
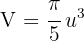
Calcule o volume do corpo gerado ao girar, em torno do eixo , a área limitada pelos gráficos de 
1Para encontrar os pontos de interseção entre a reta e a parábola, resolvemos o sistema
Igualamos as expressões e fatoramos para obter:
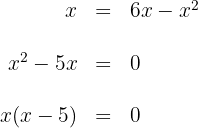
As raízes são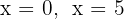 
. Logo, os pontos de interseção são: 
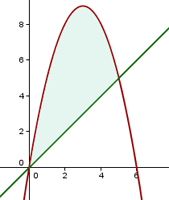
2Substituímos na fórmula para encontrar o volume:
3Desenvolvemos o integrando:
4Como se trata de uma integral definida, podemos dispensar a constante de integração:
5Avaliamos nos extremos de integração:
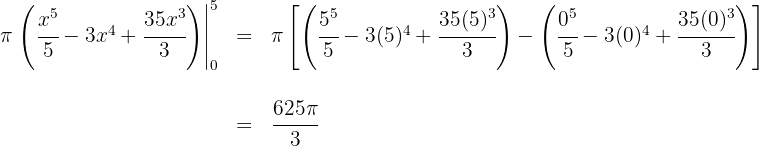
Portanto, o volume é:
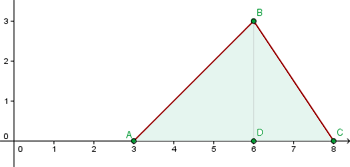
Calcule o volume gerado por um triângulo de vértices 
ao girar 
ao redor do eixo .
1Representamos graficamente
As equações das retas que passam por 
e 
são:
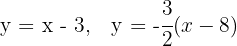
2Substituímos na fórmula para encontrar o volume, observando que, para o segmento de reta , consideramos o intervalo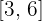 
e, para o segmento de reta , consideramos o intervalo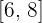 
:
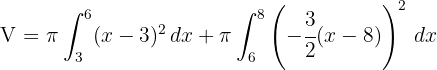
3Desenvolvemos o integrando:
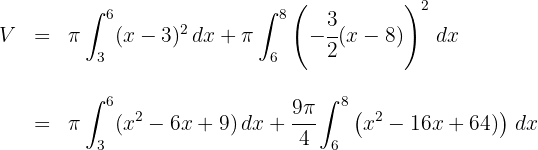
4Como se trata de integrais definidas, podemos dispensar a constante de integração:
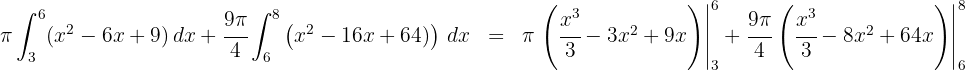
5Avaliamos nos extremos de integração e obtemos:
Logo, o volume é
Calcule o volume da figura gerada ao girar a elipse 
em torno do eixo .
1Representamos graficamente
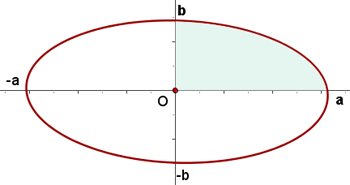
2O centro da elipse é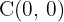 
. Os pontos de interseção com o eixo são:
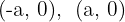
3A partir da equação da elipse, obtemos a função:
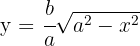
PComo a elipse é uma curva simétrica, o volume pedido é duas vezes o volume gerado pelo arco entre 
e 
.
4Substituímos na fórmula para encontrar o volume
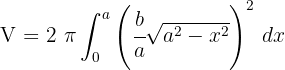
5Desenvolvemos o integrando:
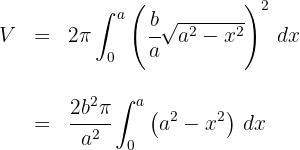
6Como se trata de uma integral definida, podemos dispensar a constante de integração:
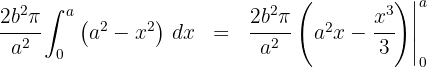
7Avaliamos nos extremos de integração:
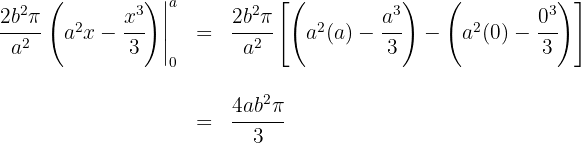
Assim, o volume é:
Calcule o volume do cilindro gerado pelo retângulo limitado pelas retas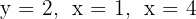 
e o eixo ao girar em torno desse eixo.
1Substituímos na fórmula para encontrar o volume:
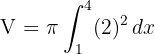
2Como se trata de uma integral definida, podemos dispensar a constante de integração:
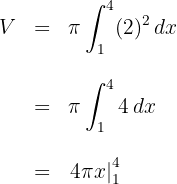
3Avaliamos nos extremos de integração:
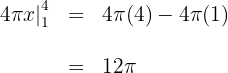
Logo, o volume é:
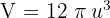
Calcule o volume da esfera de raio 
.
1Começamos pela equação da circunferência:
2Ao girar um semicírculo em torno do eixo das abscissas, obtemos uma esfera:
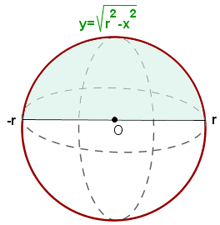
3A partir da equação da circunferência, obtemos a função:
4Substituímos na fórmula para encontrar o volume:
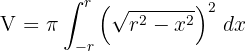
5Desenvolvemos o integrando:
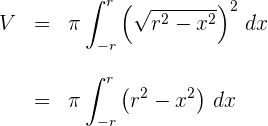
6Como se trata de uma integral definida, podemos dispensar a constante de integração:
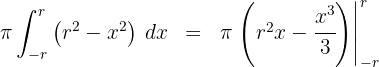
7Avaliamos nos extremos de integração:
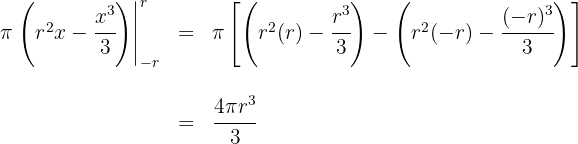
Portanto, o volume é:
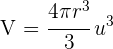
Calcule o volume gerado pela rotação da região limitada pela parábola 
e pela reta 
, em torno do eixo 
.
1Representamos graficamente:
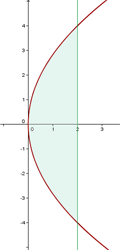
Como o giro ocorre em torno do eixo , aplicamos:
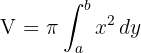
O volume será a diferença entre o volume gerado pela reta e o volume gerado pela parábola entre os extremos do intervalo.
.
Como a parábola é simétrica em relação ao eixo ,o volume é igual a duas vezes o volume gerado entre 
.
2Substituímos na fórmula para encontrar o volume:
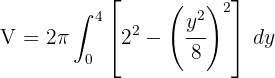
3Como se trata de uma integral definida, podemos dispensar a constante de integração:
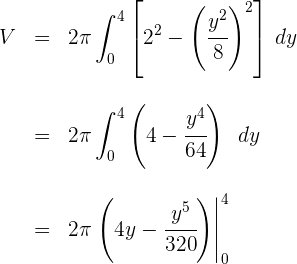
4Avaliamos nos extremos de integração:
Portanto, o volume é:
Calcule o volume do elipsoide gerado pela elipse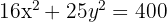 
, ao girar em torno do eixo .
1Escrevemos a elipse em sua forma ordinária:
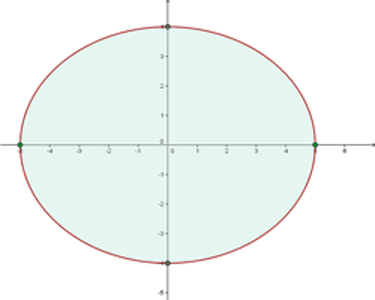
2O centro da elipse é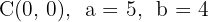 
. Aplicamos a mesma fórmula usada no exercício 9.
3Substituindo os valores conhecidos, obtemos:
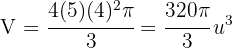
Encontre o volume do sólido de revolução gerado ao girar a função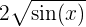 
, definida no intervalo 
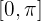, em torno do eixo OX.
1Ilustramos a função:
2Calculamos a integral:
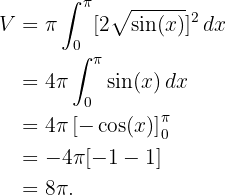
Seja 
para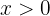 
.
a) Desenhe o gráfico de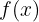 
.
b) Calcule a área da região limitada por 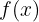e o eixo no intervalo 
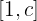, onde 
.
c) Calcule o volume do sólido de revolução gerado ao girar a região do item (b) em torno do eixo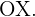 
.
d) Analise o que acontece com a área e com o volume quando (b) si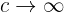 
? E o volume do sólido de revolução?
a)
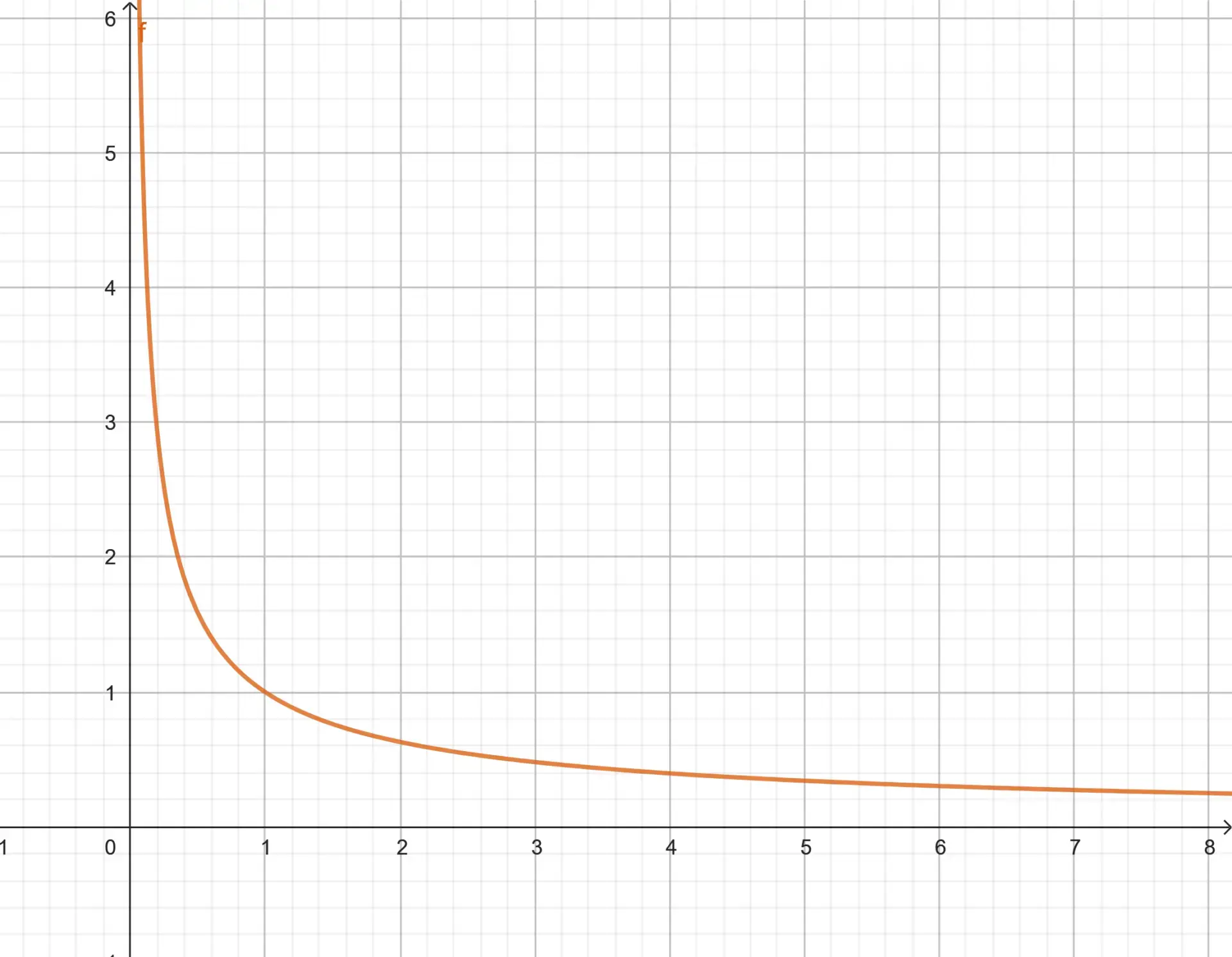
b) Calculamos a integral no intervalo 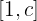. Ou seja, a área embaixo da curva:
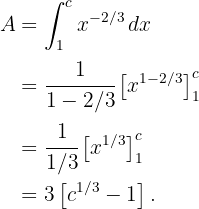
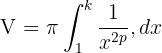OX:
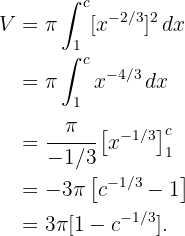
d Se no resultado obtidos (b), temos:
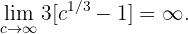
É o mesmo que falar que a área embaixo da a curva é infinita e se o intervalo que usamos va ao infinito. No entanto, notamos que:
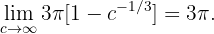
Ou seja, o volumen do sólido se mantem isolado
Gostou desse artigo? Deixe uma nota!
Loading...
