Bem-vindo ao nosso blog dedicado à fascinante e poderosa técnica matemática conhecida como “integral por partes”!
As integrais são uma parte fundamental do cálculo, mas muitas vezes podem parecer um verdadeiro desafio. A boa notícia é que você não precisa se assustar! Estamos aqui para te ajudar a entender, de forma clara e acessível, como funciona o método da integral por partes, uma ferramenta que pode transformar aquela integral complicada em algo muito mais simples.
Da física à engenharia, passando por várias outras áreas do conhecimento, é comum nos depararmos com funções que só conseguimos resolver utilizando o método da integral por partes. Neste artigo, reunimos uma seleção de exercícios resolvidos passo a passo para te ajudar a entender melhor e a praticar essa técnica essencial no estudo da matemática.
Vem com a gente e descubra como dominar de vez a integral por partes!
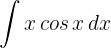
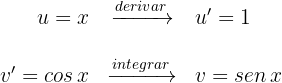
1Escolhemos  e calculamos
e calculamos  e
e 
2Substituímos os valores de  e
e  na fórmula de integral por partes:
na fórmula de integral por partes:
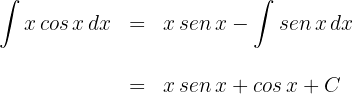
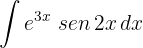
1 Escolhemos 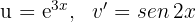 e calculamos
e calculamos  e
e 

2Substituímos os valores de  e
e  na fórmula de integral por partes:
na fórmula de integral por partes:
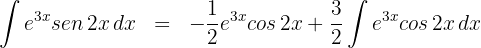
3A última integral obtida é resolvida através da integral por partes, assim, escolhemos 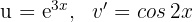 e calculamos
e calculamos  e
e 

4Substituímos os valores de  e
e  na fórmula de integral por partes e obtemos
na fórmula de integral por partes e obtemos
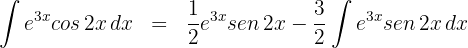
5 Substituimos o resultado obtido do passo 4, no resultado do passo 2 e resolvemos a equaão resultante
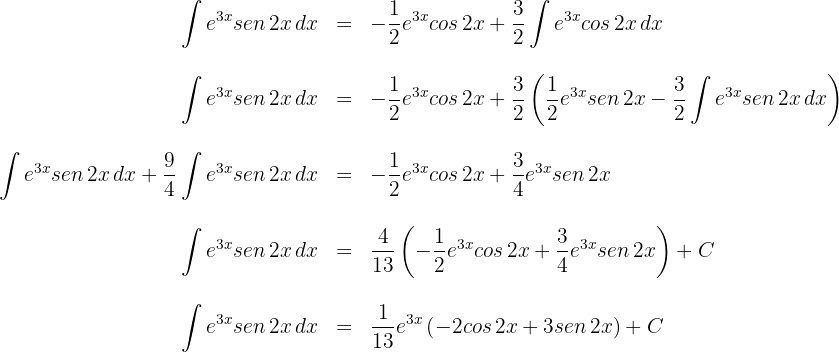
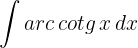
1Escolhemos 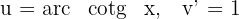 e calculamos
e calculamos  e
e 
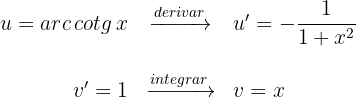
2Substituimos os valores de  e
e  na fórmula de integral por partes:
na fórmula de integral por partes:
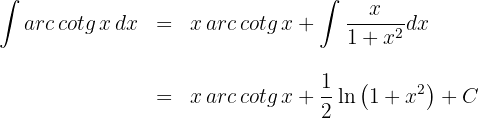
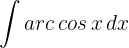
1Escolhemos  e calculamos
e calculamos  e
e 
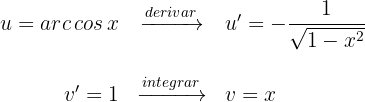
2Substituimos os valores de  e
e  na fórmula de integral por partes:
na fórmula de integral por partes:

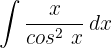
1Escolhemos 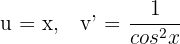 e calculamos
e calculamos  e
e 

2Sustituimos los valores de  y
y  en la fórmula de integración por partes considerando
en la fórmula de integración por partes considerando 
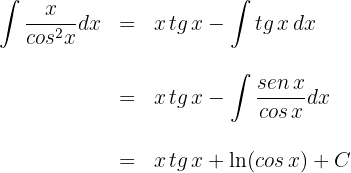

1Escolhemos  e calculamos
e calculamos  e
e 

2Substituimos os valores de  e
e  na fórmula de integral por partes:
na fórmula de integral por partes:
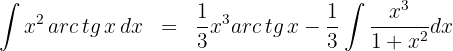
3Fazemos a divisão do novo integrando e obtemos:

4Substituimos na integral e resolvemos:


1Escolhemos 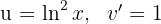 e calculamos
e calculamos  e
e 

2Substituimos os valores de  e
e  na fórmula de integral por partes:
na fórmula de integral por partes:

3A última integral obtida é resolvida através da integral por partes, assim, escolhemos 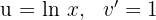 e calculamos
e calculamos  e
e 

4Substituimos os valores de  e
e  na fórmula de integral por partes e obtemos:
na fórmula de integral por partes e obtemos:

5Substituimos o resultado obtido no ítem 4, no resultado do ítem 2


1Escolhemos 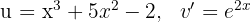 e calculamos
e calculamos  e
e 
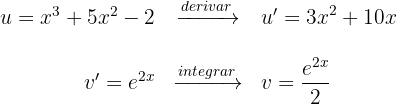
2Substituimos os valores de  e
e  na fórmula de integral por partes:
na fórmula de integral por partes:
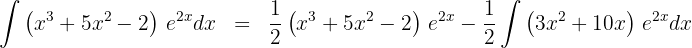
3A última integral obtida é resolvida mediante integral por partes, dessa forma, escolhemos 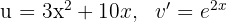 e calculamos
e calculamos  e
e 
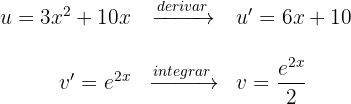
4Substituimos os valores de  e
e  na fórmula de integral por partes e vamos obter:
na fórmula de integral por partes e vamos obter:
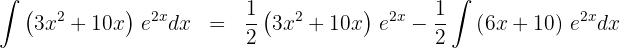
5 A última integral obtida é resolvida mediante integral por partes, assim, escolhemos 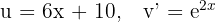 y calculamos
y calculamos  y
y 

6Substituimos os valores de  e
e  na fórmula de integral por partes e obtemos:
na fórmula de integral por partes e obtemos:
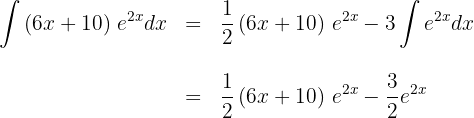
7Substituimos o resultado obtido no ítem 6, no resultado do ítem 4:

8Substituimos o resultado obtido no ítem 7, no resultado do ítem 2:
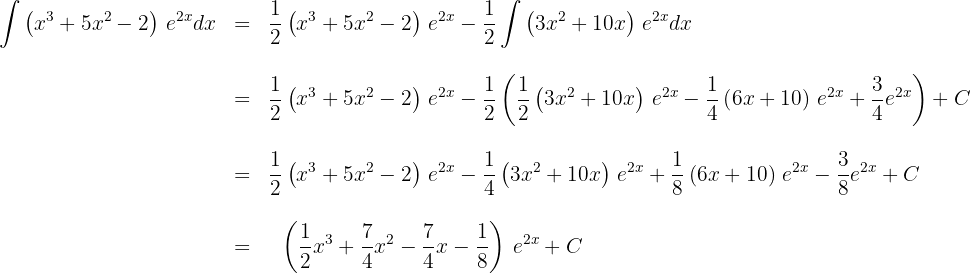
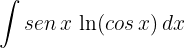
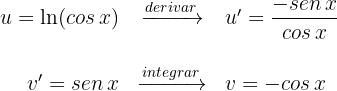
1Escolhemos 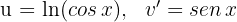 e calculamos
e calculamos  e
e 
2Substituimos os valores de  e
e  na fórmula de integral por partes:
na fórmula de integral por partes:
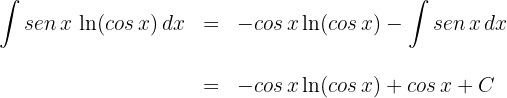
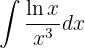
1Escolhemos  e calculamos
e calculamos  e
e 

2Substituimos os valores de  e
e  na fórmula de integral por partes:
na fórmula de integral por partes:
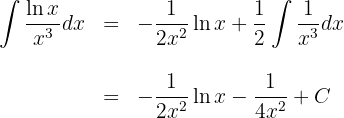
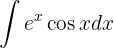
1Escolhemos 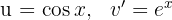 e calculamos
e calculamos  e
e 

2Substituimos os valores de  e
e  na fórmula de integral por partes:
na fórmula de integral por partes:
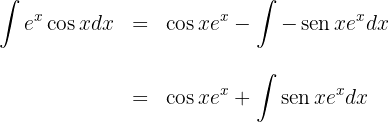
3A última integral obtida é resolvida mediante a integral por partes, sendo assim,escolhemos  e calculamos
e calculamos  e
e 

4Substituimos os valores de  e
e  na fórmula de integral por partes e obtemos:
na fórmula de integral por partes e obtemos:
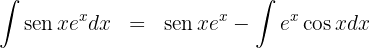
5Substituimos o resultado obtido do ítem 4, no resultado do ítem 2 e resolvemos a equação resultante:

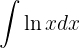
1Escolhemos 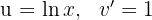 e calculamos
e calculamos  e
e 
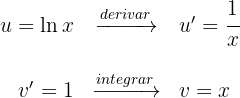
2Substituimos os valores de  e
e  na fórmula de integral por partes:
na fórmula de integral por partes:
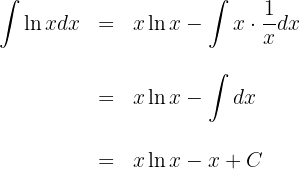
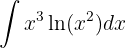
1Escolhemos 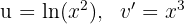 e calculamos
e calculamos  e
e 

2Substituimos os valores de  e
e  na fórmula de integral por partes:
na fórmula de integral por partes:


1Escolhemos  e calculamos
e calculamos  e
e 

2Substituimos os valores de  e
e  na fórmula de integral por partes:
na fórmula de integral por partes:


1Escolhemos 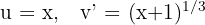 e calculamos
e calculamos  e
e 
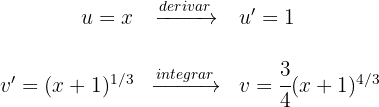
2Substituimos os valores de  e
e  na fórmula de integral por partes:
na fórmula de integral por partes:
Resumir com IA:


