
Determine a equação do plano
Considerando as retas:

Determine a equação do plano que contém a reta  e é paralelo a
e é paralelo a  .
.
Lembrando que um plano é determinado por um ponto e dois vetores diretores.
Resolvendo o sistema:
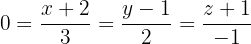 vamos obter que: A=(-2,1,-1) é um ponto da reta
vamos obter que: A=(-2,1,-1) é um ponto da reta  e portanto,
e portanto,
pertence ao plano.
Um ponto no plano é: 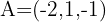
Os vetores diretores são:
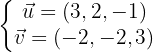
Por fim, a equação do plano é dada pelo seguinte determinante:
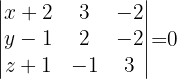
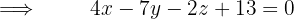
Encontre a equação do plano que contenha as retas abaixo:

Lembrando que um plano é determinado por um ponto e dois vetores diretores.
Vamos resolver:
 temos que A=(-2,1,-3) é um ponto da reta
temos que A=(-2,1,-3) é um ponto da reta  e portanto, pertence ao plano.
e portanto, pertence ao plano.
Um ponto no plano é: 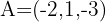
Os vetores geradores são:
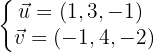
Portanto, a equação do plano é dada pelo seguinte determinante:

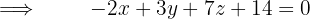
Determine a equação do plano que passa pelo ponto A(2, 5, 1) e pela reta de equação:
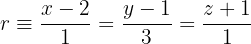
Através da parametrização, obtemos que o vetor diretor é 
Resolvendo o sistema:
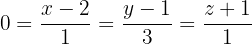 obtemos que B(2,1,-1) é um ponto da reta
obtemos que B(2,1,-1) é um ponto da reta  .
.
Portanto, o outro vetor diretor é dado por:

Um ponto no plano é: A(2, 5, 1)
Os vetores diretores são:
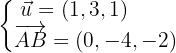
Dessa forma, a equação do plano é dada pelo seguinte determinante:
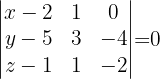
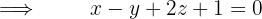
Encontre a equação do plano que contenha a reta  e seja paralela à reta.
e seja paralela à reta.
A partir da equação contínua da reta que está contida no plano e da equação paramétrica da reta paralela, obtemos dois vetores diretores do plano.
Um ponto no plano é: A(2, 2, 4)
Os vetores diretores sã0:
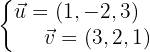
Assim, a equação do plano é dada conforme o determinante:
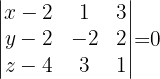
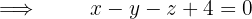
Problemas variados da equação do plano
Encontre a equação do plano que passe pelos pontos A(1, −2, 4), B(0, 3, 2) e seja paralela à reta 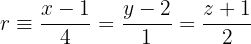 .
.
Um dos vetores diretores do plano será o vetor diretor da reta  .
.
O outro vetor é:
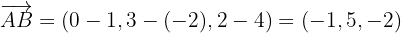
Um ponto no plano é: A(1, −2, 4)
Os vetores diretores são:
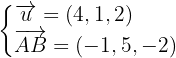
Portanto, a equação do plano é dada pelo seguinte determinante:

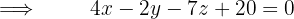
Considere π um plano que passe por P(1, 2, 1) e intercepta os semieixos coordenados positivos nos pontos A, B e C. Sabendo que o triângulo ABC é equilátero, determinar as equações do plano π.
Lembremos que, se conhecemos os pontos em que um plano intercepta os eixos coordenados, temos:
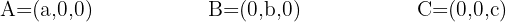
A equação do plano na forma dos interceptos é dada por:

Como o triângulo é equilátero, os três segmentos dos semieixos positivos, desde a origem até os pontos de interseção, são iguais. Assim, a equação fica:

Para encontrar o valor de  basta substituir as coordenadas do ponto P(1, 2, 1) na equação:
basta substituir as coordenadas do ponto P(1, 2, 1) na equação:

Portanto, a equação do plano é:
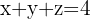
Encontre as equações dos eixos coordenados e planos coordenados.
1. Eixo OX
Ponto pertencente à reta: O(0,0,0): O(0,0,0)
Vetor diretor: 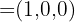
Equação simétrica da reta:

Equação reduzida:
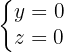
2. Eixo OY
Ponto pertencente à reta: O(0,0,0)
Vetor diretor: 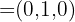
Equação simétrica da reta:

Equação reduzida:
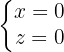
3. Eixo OZ
Ponto pertencente à reta: O(0,0,0)
Vetor diretor: 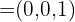
Equação simétrica da reta:
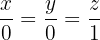
Equação reduzida:
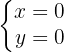
4. Plano XY
Ponto pertencente ao plano: O(0,0,0)
Vetores diretores:
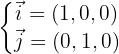
Portanto, a equação do plano é dada pelo seguinte determinante:
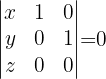

5. Plano XZ
Ponto pertencente ao plano: O(0,0,0)
Vetores diretores:
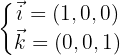
Portanto, a equação do plano é dada pelo seguinte determinante:


6. Plano YZ
Ponto pertencente ao plano: O(0,0,0)
Vetores diretores:
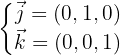
Portanto, a equação do plano é dada pelo seguinte determinante:


Encontre as coordenadas da interseção entre o plano  e a reta definida pelo ponto (1, −3, 2) e o vetor
e a reta definida pelo ponto (1, −3, 2) e o vetor 
1. Obtemos a equação da reta descrita
Com o vetor diretor e o ponto que pertence à reta, sua equação paramétrica é:
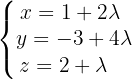
2. Substituímos na equação do plano
Queremos encontrar o ponto que pertence tanto à reta quanto ao plano, então suas coordenadas devem satisfazer ambas as equações. Substituímos as coordenadas paramétricas na equação do plano:

Eliminamos os parênteses:

Simplificamos e isolamos 

3. Calculamos as coordenadas usando o valor de 
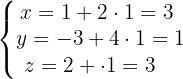
Portanto, as coordenadas do ponto de interseção são: (3,1,3)
Determine a equação reduzida do plano que passe pelo ponto P(1, 1, 1) e seja paralelo a:
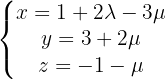
A partir da equação simétrica do plano ao qual ele é paralelo, obtemos dois vetores diretores:
Vetores diretores:
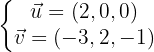
Um ponto no plano: P(1,1,1)
Portanto a equação do plano é dada pelo determinante:
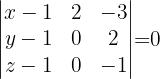
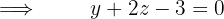
Encontre a equação do plano paralelo às retas das equações: 
e que passe pelo ponto (1, 1, 2).
1. Obtenha a equação paramétrica de 
Para cada uma das retas paralelas, vamos obter um vetor diretor. No entanto, não é possível obter essa informação através da equação reduzida de  . Por isso, devemos fazer sua equação paramétrica.
. Por isso, devemos fazer sua equação paramétrica.
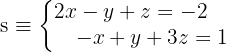
a. Isolamos uma das variáveis (do outro lado da equação)
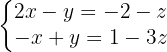
b. Método de Cramer para resolver  e
e  em função de
em função de 
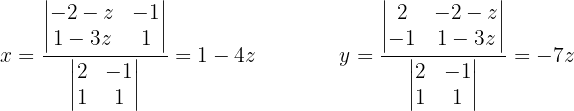
c. Conseguimos 2 pontos na reta atribuindo valores a 


d. Determinamos o vetor diretor da reta 
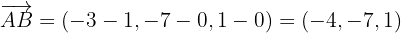
Assim, usando o ponto  sobre a reta
sobre a reta 
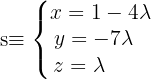
2. Determinamos a equação do plano
Ponto no plano: A(1, 1, 2)
Vetores diretores são:
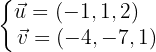
Portanto, a equação do plano é dada pelo determinante:
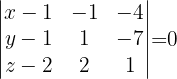
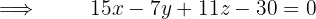
Resumir com IA:












