O que é a média aritmética?
Na matemática, a média aritmética é encontrada através da soma dos valores de números reais de um conjunto e dividida pelo número total de números reais. Por exemplo, se quisermos saber a nota média que os alunos de uma turma obteve, primeiro, temos que somar as pontuações de todos eles, então, dividir pelo número de alunos da turma e, desta forma, vamos obter a nota média que a turma alcançou.
Exercícios resolvidos de média aritmética
Considerando as seguintes informações: 
.
a) Calcule a média.
b) Se multiplicarmos todos os números anteriores por 
. Qual vai ser a nova média?
Considere os seguintes dados: .
a) Calcule a sua média:
A média 
de um conjunto de dados é dada pela soma dos dados entre o número total de dados. Desta forma:
b) Se multiplicarmos todos os dados anteriores por 3, qual será a nova média?
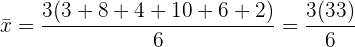
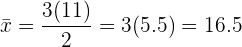
Podemos observar que, se todos os índices são multiplicados por , então a média aritmética fica multiplicada por . Portanto, é possível representar esta observação de acordo com a seguinte propriedade que a média aritmética satisfaz.
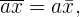
sendo 
uma constante.
A um conjunto de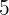 
números cuja média é 
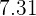são adicionados os números
e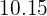 
. Qual é a média do novo conjunto de números?
A um conjunto de 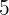números cuja média é 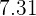foi adicionado os números e 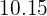. Qual é a média do novo conjunto de números?
A primeira coisa que sabemos é
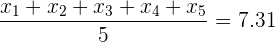
Agora, vamos calcular a média do conjunto de 7 números e desenvolver conforme segue:
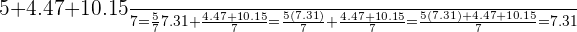
Desta forma, a média aritmética fica sendo a mesma.
Calcule a média de uma distribuição estatística que é dada pela seguinte tabela:
| xi | 61 | 64 | 67 | 70 | 73 |
|---|---|---|---|---|---|
| fi | 5 | 18 | 42 | 27 | 8 |
A tabela indica a variável 
e o número de vezes que se repete no conjunto de dados 
, e, por essa razão, vamos completar a tabela com o resultado da variável pela sua frequência absoluta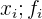 
com a finalidade de obter a soma de todos os valores que se repetem vezes, e, desta forma, poderão ser somados, finalmente, a todos eles e ser divididos entre a quantidade de dados que foram gerados. Observe a fórmula:
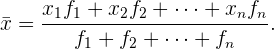
Aqui está a análise numérica:
| xi | fi | xi · fi |
|---|---|---|
| 61 | 5 | 305 |
| 64 | 18 | 1152 |
| 67 | 42 | 2814 |
| 71 | 27 | 1890 |
| 73 | 8 | 584 |
| 100 | 6745 |
Então, basta realizar a divisão.
E vamos chegar ao resultado desejado.
Encontre a média da distribuição estatística que é dada pela seguinte tabela:
| fi | |
|---|---|
| [10, 15) | 3 |
| [15, 20) | 5 |
| [20, 25) | 7 |
| [25, 30) | 4 |
| [30, 35) | 2 |
Primeiramente, observe que agora os dados não são representados da mesma forma que antes, temos intervalos de valores. Neste caso, o que é feito é calcular algo chamado de marca de classe. 
. Isso consiste em calcular a média entre os dois valores que definem o intervalo, por exemplo:
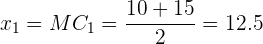
e assim sucessivamente com os outros intervalos.
Uma vez feito o cálculo, completamos a tabela com o produto da variável pela sua frequência absoluta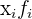 
para calcular a média aritmética
| xi | fi | xi · fi | |
|---|---|---|---|
| [10, 15) | 12.5 | 3 | 37.5 |
| [15, 20) | 17.5 | 5 | 87.5 |
| [20, 25) | 22.5 | 7 | 157.5 |
| [25, 30) | 27.5 | 4 | 110 |
| [30, 35) | 32.5 | 2 | 65 |
| 21 | 457.5 |
Calculamos a soma da variável pela sua frequência absoluta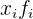 
que é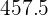 
e então, dividimos pelo total de dados 
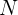que é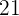 
. Desta forma,
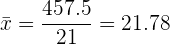
Os resultados que vamos ter ao lançar um dado.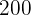 
vezes são representadas pela tabela a seguir.
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| fi | a | 32 | 35 | 33 | b | 35 |
Determinar 
e 
sabendo que a pontução média é 
.
Através dos dados informados, podemos construir a seguinte tabela
| xi | fi | xi · fi |
|---|---|---|
| 1 | a | a |
| 2 | 32 | 64 |
| 3 | 35 | 125 |
| 4 | 33 | 132 |
| 5 | b | 5b |
| 6 | 35 | 210 |
| 135 + a + b | 511 + a + 5b |
A soma dos dados da coluna 
nos dá o resultado
O anterior vamos igualar a 200, que é uma das hipóteses do problema. Sendo assim,
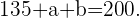
Simplificando, vamos obter como primeira equação:
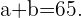
Agora, vamos calcular a média da distribuição e vamos igualar a 3.6, de acordo com o valor que é indicado no enunciado do problema
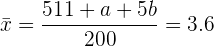
Simplificando novamente, vamos obter a segunda equação:
Desta forma, vamos ter o seguinte sistema de equações:
Resolvemos isso pelo método de eliminação
.
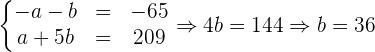Ou seja,
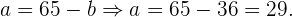
Desta forma, concluímos qu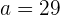e:
e 
Calcule a média da distribuição estatística:
| fi | |
|---|---|
| [0, 5) | 3 |
| [5, 10) | 5 |
| [10, 15) | 7 |
| [15, 20) | 8 |
| [20, 25) | 2 |
| [25, ∞) | 6 |
Vamos começar calculando a 
| xi | fi | |
|---|---|---|
| [0, 5) | 2.5 | 3 |
| [5, 10) | 7.5 | 5 |
| [10, 15) | 12.5 | 7 |
| [15, 20) | 17.5 | 8 |
| [20, 25) | 22.5 | 2 |
| [25, ∞) | --- | 6 |
| 31 |
E aqui observamos que NÃO é possível calcular a média porque não é possível encontrar a marca de classe do último intervalo.
Considere as seguintes informações: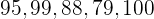 
.
a) Calcule sua média.
b) Se adicionarmos 6 a todos os dados anteriores, qual será a nova média?
Considerando os seguintes dados: .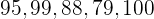
a) Calcule sua média.
A média de um conjunto de dados é dada pela soma dos dados dividida pelo número total de dados. Desta forma,
b) Se adicionarmos 
a todos os dados anteriores, qual será a nova média?
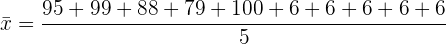
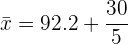
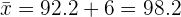
Vamos observar que, se somarmos a todos os dados, então a média aritmética fica somada por . Desta forma, é possível representar esta observação conforme a propriedade que a média aritmética satisfaz é a seguinte:
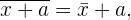
tendo como constante.
A altura em cm dos 
jogadores que começaram um jogo de vôlei, separados por times, são conforme segue:
Time 1: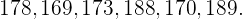 
Time 2: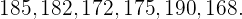 
a) Calcule a média aritmética de cada time.
b) Calcule a média aritmética do jogo.
A altura em cm dos jogadores que começaram o jogo vôlei, separados por time, são as seguintes:
Time 1: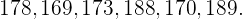
Time 2: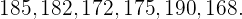
a) Calcule a média aritmética de cada time.
Time 1:
Time 2:
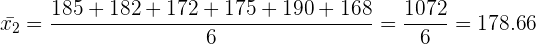
b) Calcule a média aritmética do jogo.
Para calcular a média aritmética do jogo, , calculamos a média aritméticas das médias 
e 
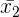. Desta forma,
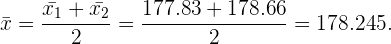
A mediana de um conjunto de dados é de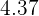 
. Se forem adicionados 
dados, um dos quais é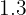 
, qual valor o segundo dado deve ter para que a média seja mantida?
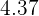A mediana de um conjunto de dados é de . Se forem adicionados dados, um dos quais é 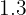, qual valor o segundo dado deve ter para que a média seja mantida?
Para que a média do conjunto de dados seja mantida, os dois dados adicionados devem satisfazer que a sua média seja igual a 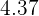. Sabemos que um deles é 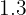. Vamos chamar o segundo dado de "". Portanto, o que procuramos é que:
Vamos resolver essa equação de primeiro grau:
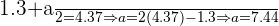
Desta forma, o segundo dado deve ser 
. Podemos verificar facilmente que a média continua sendo :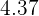
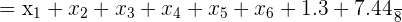
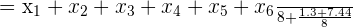
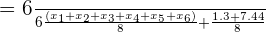
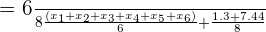
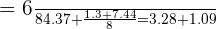
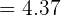
Calcule a média dos primeiros 
múltiplos de 
. Generalize o resultado anterior para calcular a média dos primeiros 
múltiplos de .
Calcule a média dos primeiros múltiplos de . Generalizar o resultado anterior para calcular a média dos primeiros múltiplos de .
Os primeiros múltiplos de são:
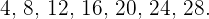
Desta forma, sua média aritmética é:
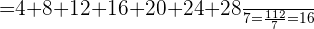
Para generalizar o resultado anterior, nota-se que o enésimo múltiplo de é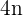 
. Sendo assim, a média é:
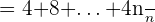
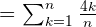
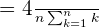
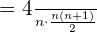
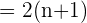
Tendo como valor 
da expressão obtida acima, vamos obter o resultado da primeira parte do exercício.
Gostou desse artigo? Deixe uma nota!
Loading...
