O que representa a integral definida e como a calculamos?
Vamos relembrar que o Teorema Fundamental do Cálculo diz que a integral definida pode ser calculada utilizando:

onde  é qualquer função primitiva de
é qualquer função primitiva de  .
.
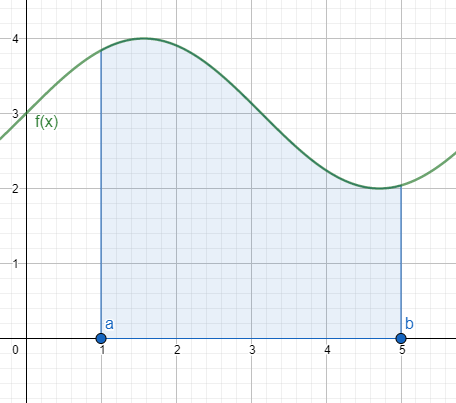
Além disso, vamos lembrar que a integral definida representa a área sob a curva de  entre os pontos
entre os pontos  e
e  , conforme pode ser observado na figura a seguir:
, conforme pode ser observado na figura a seguir:
Exercícios propostos
Resolva as seguintes integrais definidas:
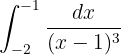
A primeira integral pode ser resolvida utilizando a fórmula da integral de uma potência. Observe primeiro que:

Assim, podemos utilizar a fórmula:
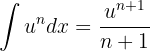
com a substituição de variável 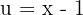 e
e  (observe que em integrais definidas não é necessário adicionar a constante de integração). Dessa forma, obtemos:
(observe que em integrais definidas não é necessário adicionar a constante de integração). Dessa forma, obtemos:
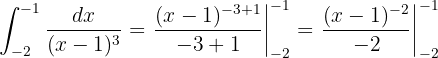
Ou seja,
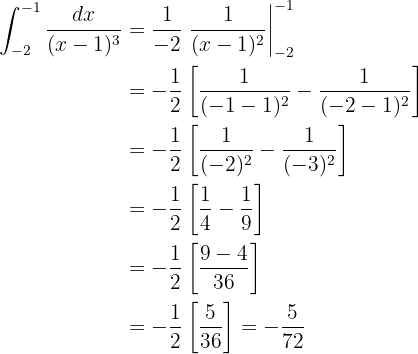
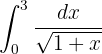
Assim como no caso anterior, esta integral é resolvida com a fórmula da integral de uma potência:

simplificamos um pouco,
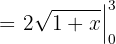
E agora avaliamos nos limites da integral:
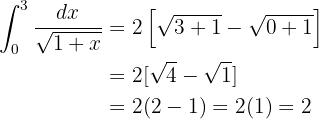
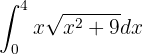
Esta integral é resolvida com uma substituição de variável. Observe que dentro da raiz temos: 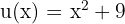 . Derivamos:
. Derivamos: 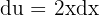 ; e ao isolar:
; e ao isolar:  , temos:
, temos:

Além disso, como faremos uma substituição de variável, também devemos ajustar os limites da integral. Em especial:
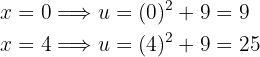
Portanto, a integral é convertida em:
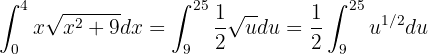
Agora, resolvemos a integral utilizando a fórmula da integral de uma potência:
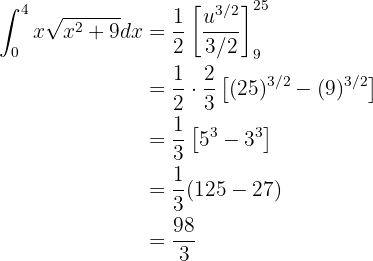
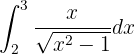
Assim como no caso anterior, fazemos a seguinte substituição da variável:

Fazendo a derivação, temos: 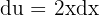 . Portanto, quando isolamos
. Portanto, quando isolamos  (já que é o que aparece no integrando), obtemos:
(já que é o que aparece no integrando), obtemos:

Agora, ajustamos os novos limites da integral:
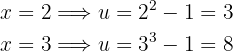
Por tanto, a integral se transforma em:

Integramos usando a fórmula da integral de uma potência:
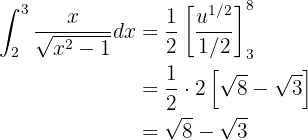
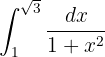
Essa integral é resolvida rapidamente ao lembrar que:

Portanto, a integral definida é resolvida imediatamente:
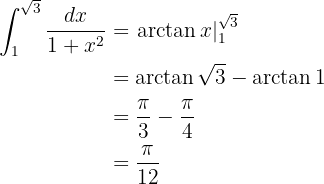
Lembre-se que: 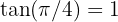 e
e 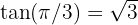 (conhecer esses valores ajuda quando queremos encontrar os valores da função arco-tangente).
(conhecer esses valores ajuda quando queremos encontrar os valores da função arco-tangente).
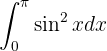
Para resolver essa integral, precisamos usar uma identidade trigonométrica. Em particular, como temos 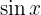 elevado a uma potência par (2 neste caso), usamos uma identidade para reduzir a potência impar. Essa identidade é derivada da fórmula do ângulo duplo para o cosseno:
elevado a uma potência par (2 neste caso), usamos uma identidade para reduzir a potência impar. Essa identidade é derivada da fórmula do ângulo duplo para o cosseno:
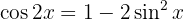
que, ao isolar,  , obtemos:
, obtemos:
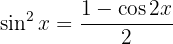
Dessa forma, a integral se transforma em:
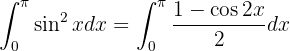
Agora, essa integral pode ser resolvida com mais facilidade:
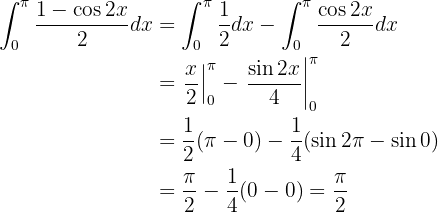
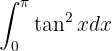
É um pouco difícil encontrar diretamente uma função (por meio de teste - erro e acerto)  tal que
tal que  ). Por isso, é melhor reescrever
). Por isso, é melhor reescrever 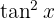 utilizando uma identidade trigonométrica. Ou seja,
utilizando uma identidade trigonométrica. Ou seja,
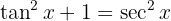
Logo 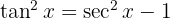 .Assim, a integral se transforma em:
.Assim, a integral se transforma em:

Sabemos que:
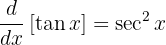
Então, a integral pode ser resolvida diretamente:
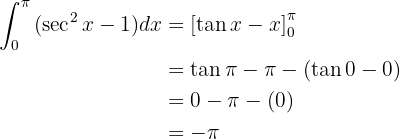
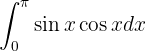
Para essa integral, não é necessário utilizar identidade trigonométrica, uma vez que nem 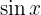 nem
nem  estão elevados a nenhuma potência. Portanto:
estão elevados a nenhuma potência. Portanto:
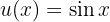
Logo,
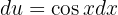
Observe que essa substituição não é injetora (um para um) no intervalo de integração. Portanto, é necessário retornar à variável original antes de avaliar:
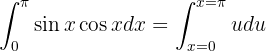
Calculamos a primitiva:

Retornando à variável original:

Agora avaliamos nos limites da integral:

Esse é o resultado que procurávamos.
Observação: se tivéssemos escolhido  também conseguiríamos resolver a integral com facilidade.
também conseguiríamos resolver a integral com facilidade.
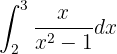
Observe que nesta integral também podemos aplicar uma substituição de variável. Em particular:

que continua em 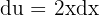 . Portanto,
. Portanto,

Além disso,
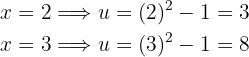
Assim, a integral se transforma em:

Ao resolver e avaliar, obtemos o valor final da integral.
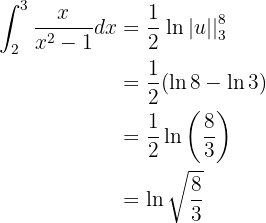

Embora não pareça de imediato, essa integral também pode ser resolvida com uma substituição de variável.
(Observe que nem toda integral exige substituição de variável, mas neste caso ela funciona bem). Veja o exemplo abaixo:
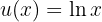
Assim,
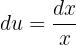
Portanto, a integral se transforma em:
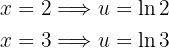
Portanto, a integral também e transforma em:
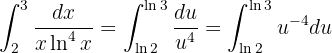
Agora. resolver a integral e avaliar nos limites dados:
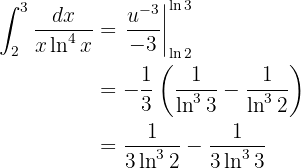
E é a forma mais simples possível que pode ficar.
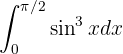
Nesta integral temos uma potência ímpar de 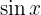 . Vamos fazer uma substituição de variável, onde
. Vamos fazer uma substituição de variável, onde 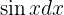 será a parte do diferencial dessa nossa variável. Portanto, separamos da seguinte maneira:
será a parte do diferencial dessa nossa variável. Portanto, separamos da seguinte maneira:
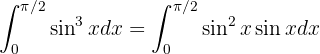
Agora utilizamos a identidade trigonométrica: 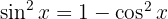 para obter:
para obter:

Fazemos a substituição:  , logo,
, logo, 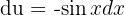 , assim:
, assim:

Além disso, essa substituição é válida pois a função é injetiva no intervalo de integração, uma vez que:
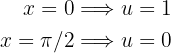
Deste modo, a integral se transforma em:

E, resolvendo a integral, temos:
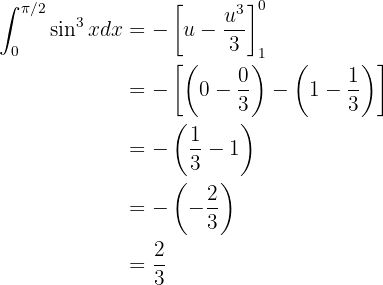
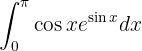
Aqui, podemos ver imediatamente que é possível aplicar uma substituição de variável:
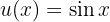
logo 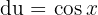 . Dessa forma, a integral se transforma em:
. Dessa forma, a integral se transforma em:

Ao integrar, temos:
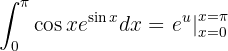
Retornamos à variável original e avaliamos nos limites.
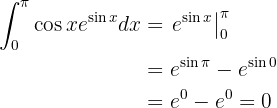
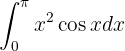
Essa integral é resolvida por integração por partes. Primeiro resolvemos a integral e depois avaliamos nos limites:

Como temos um polinômio multiplicando  , escolhemos
, escolhemos  e
e  . Assim:
. Assim:
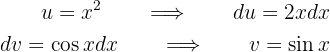
Portanto, a integral passa a ser:
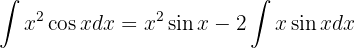
Repetimos o procedimento, dessa vez com:
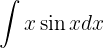
e escolhemos  e
e 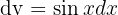 . Temos:
. Temos:
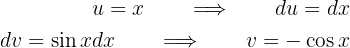
Logo, essa segunda integral se transforma:
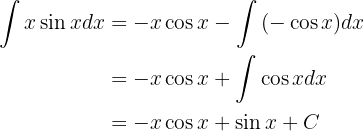
Substituindo na integral original, temos:
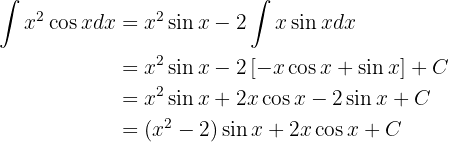
Agora que temos a integral indefinida, fazemos a avaliação nos limites de integração:
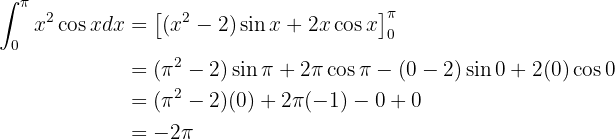
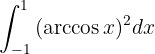
Resolver integrais com funções trigonométricas inversas pode ser mais trabalhoso. Geralmente, tentamos uma substituição de variável como:
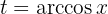
(mesmo que nem sempre funcione). Isolando  , temos
, temos 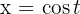 . Portanto,
. Portanto,
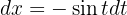
Continuamos da seguinte forma:
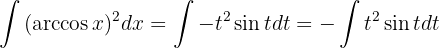
Essa integral também é resolvida por integração por partes. Começamos com:  e
e 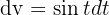 , por tanto
, por tanto
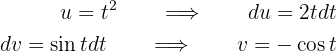
Assim, a integral se transforma em:

Agora aplicamos 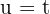 e
e  , así,
, así,
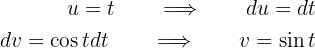
Com isso, a integral se torna:
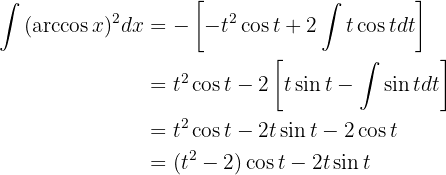
Agora, podemos retornar à variável original ou trocar os limites da integral. Vamos optar pela segunda opção:
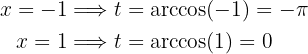
Dessa forma, a integral é:
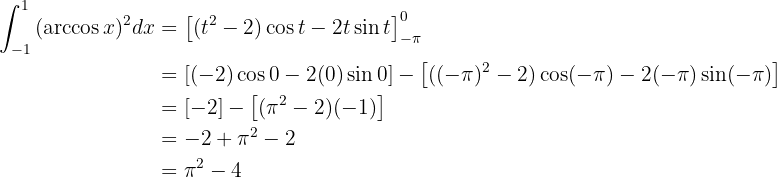

Por fim, essa integral será resolvida com uma substituição de variável, com o objetivo de eliminar a raiz. Tomamos: 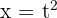 , deste modo:
, deste modo:
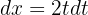
Consideramos 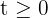 . Assim,
. Assim, 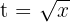 e
e
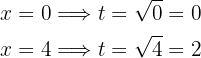
Assim, a integral se transforma em:

Note que podemos reescrever o integrando para facilitar a integração. Observe:
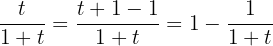
Assim, temos:
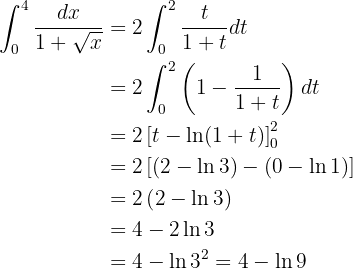
Esse é o resultado final da integral.