Seja bem-vindo e bem-vinda à nossa seção dedicada à resolução de problemas utilizando o método de integração por substituição. Essa técnica, também conhecida como mudança de variável, é uma ferramenta fundamental no cálculo integral e permite lidar com uma ampla variedade de funções de forma mais eficiente.
Vamos guiá-lo por meio de exercícios resolvidos que mostram como escolher substituições adequadas para simplificar expressões complexas. Cada exemplo inclui uma explicação passo a passo da estratégia adotada, desde a escolha da substituição até a aplicação da regra da cadeia e a resolução final da integral.
A técnica de substituição é essencial para resolver integrais mais desafiadoras, e dominá-la abrirá caminho para enfrentar sem medo os diversos tipos de problemas matemáticos. Acompanhe-nos nesta jornada de aprendizado em que exploraremos a utilidade da integração por substituição e desenvolveremos, juntos, as habilidades necessárias para resolver integrais com confiança.

1 Realizamos a mudança de variável e calculamos o diferencial:
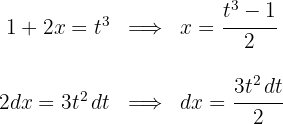
2Substituímos na integral e simplificamos:
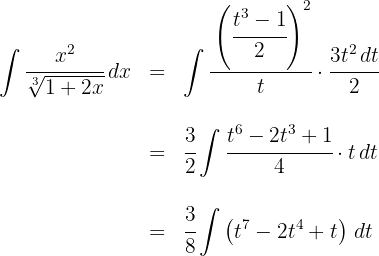
3Resolvemos a integral obtida:
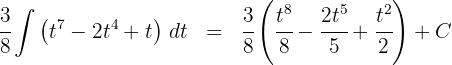
4Voltamos para a variável inicial, para tal, usamos 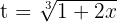

Assim, a solução em termos da variável inicial é:
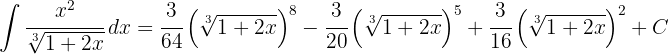
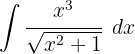
1 Realizamos a mudança de variável e calculamos o diferencial:
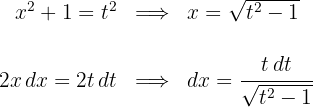
2Substituímos na integral e simplificamos:

3Resolvemos a integral obtida:
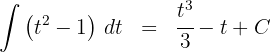
4Voltamos para a variável inicial, para tal, usamos 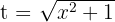
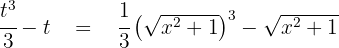
Assim, a solução em termos da variável inicial é:


1Realizamos a mudança de variável e calculamos o diferencial:
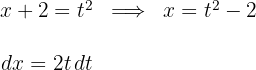
2Substituímos na integral e simplificamos
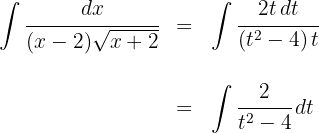
3Resolvemos a integral obtida empregando as frações parciais:
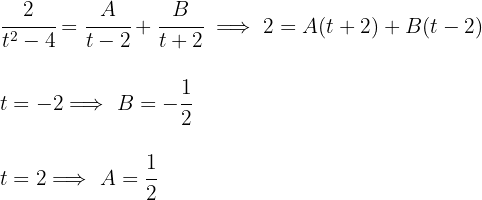
A integral é:

4Voltamos para a variável inicial, para tal, usamos 
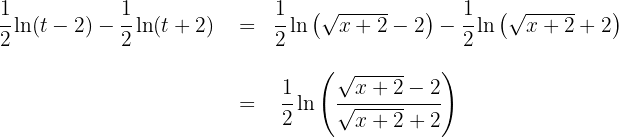
Assim, a solução em termos da variável inicial é:

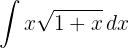
1Realizamos a mudança de variável e calculamos o diferencial:

2Substituímos na integral e simplificamos:
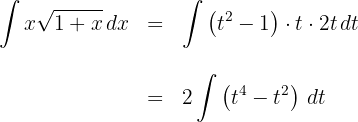
3Resolvemos a integral obtida:
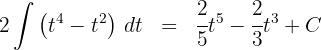
4Voltamos para a variável inicial, para tal, usamos 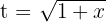
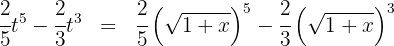
Assim, a solução em termos da variável inicial é:
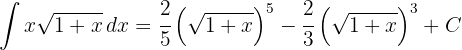
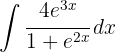
1Realizamos a mudança de variável e calculamos o diferencial:

2Substituímos na integral e simplificamos:
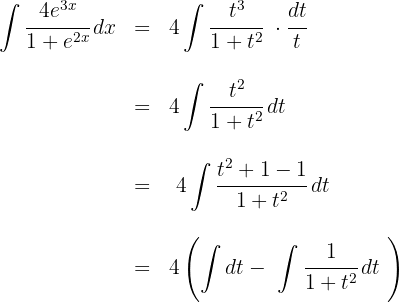
3Resolvemos a integral obtida:

4Voltamos para a variável inicial, para tal, usamos 
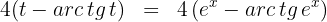
Assim, a solução em termos da variável inicial é:
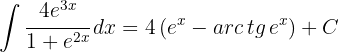

1Realizamos a mudança de variável e calculamos o diferencial:
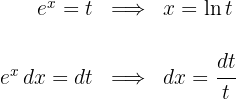
2Substituímos na integral e simplificamos:

3Resolvemos a integral obtida:
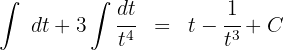
4Voltamos para a variável inicial, para tal, usamos 

Assim, a solução em termos da variável inicial é:
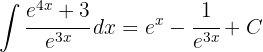
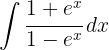
1Realizamos a mudança de variável e calculamos o diferencial:
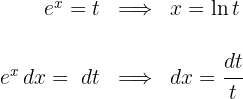
2Substituímos na integral e simplificamos:
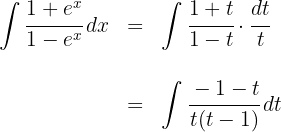
3Resolvemos a integral obtida utilizando frações parciais:
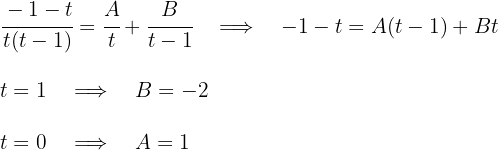
A integral é:
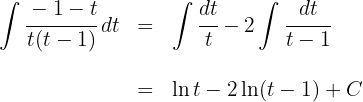
4Voltamos para a variável inicial, para tal, usamos 
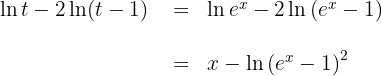
Assim, a solução em termos da variável inicial é:


1Realizamos a mudança de variável e calculamos o diferencial:


2Substituímos na integral e para simplificar utilizamos identidades trigonométricas:

3Resolvemos as integrais obtidas:

4Voltamos para a variável inicial, para isso isolamos  na mudança de variável inicial.
na mudança de variável inicial.

Calculamos o seno e cosseno de  :
:


Assim, o resultado se expressa em termos da variável  como:
como:
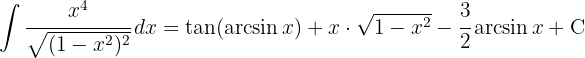

1Realizamos a mudança de variável e calculamos o diferencial:

2Substituímos na integral e simplificamos:
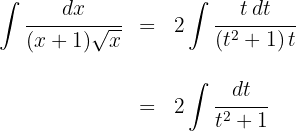
3Resolvemos a integral obtida:
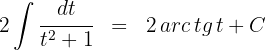
4Voltamos para a variável inicial, para tal, usamos 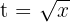
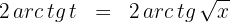
Assim, a solução em termos da variável inicial é:
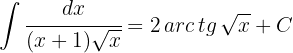

1Realizamos a mudança de variável e calculamos o diferencial
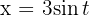
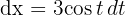
2Substituímos na integral e para simplificar utilizamos identidades trigonométricas

3Resolvemos as integrais obtidas
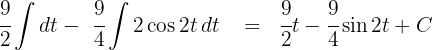
4Voltamos para a variável inicial, para isso isolamos  na mudança de variável inicial.
na mudança de variável inicial.

Calculamos o seno e cosseno de 
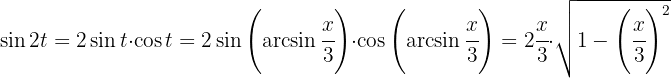
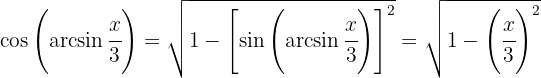
Dessa forma, o resultado é expresso na variável  como:
como:
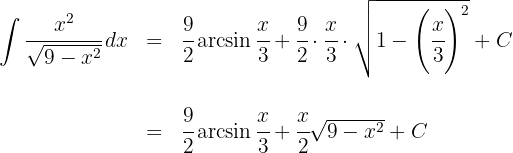

1Realizamos a mudança de variável e calculamos o diferencial:


2Substituímos na integral e simplificamos:
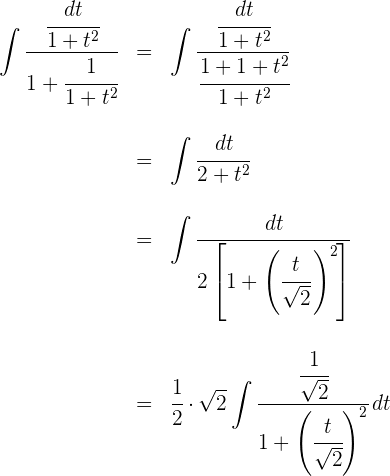
3Resolvemos as integrais obtidas:

4Voltamos para a variável inicial:
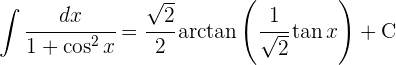
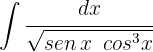
1Realizamos a mudança de variável e calculamos o diferencial:
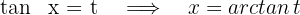

2Substituímos na integral e simplificamos:
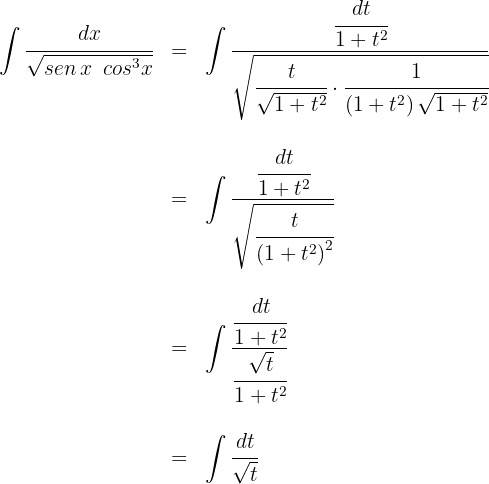
3Resolvemos as integrais obtidas:

4Voltamos para a variável inicial:
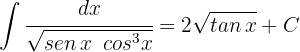

1Realizamos a mudança de variável e calculamos o diferencial:


2Substituímos na integral e simplificamos:

3Resolvemos as integrais obtidas:

4Voltamos para a variável inicial:


1Realizamos a mudança de variável e calculamos o diferencial:

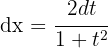
2Substituímos na integral e simplificamos:
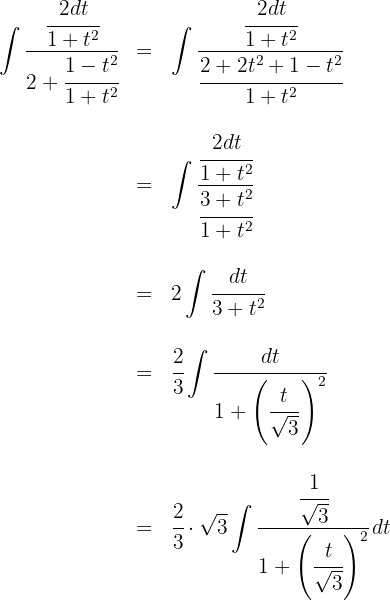
3Resolvemos as integrais obtidas:

4Voltamos para a variável inicial:

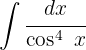
1 Realizamos a mudança de variável e calculamos o diferencial
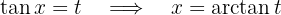

2Substituímos na integral e simplificamos

3Resolvemos las integrales obtidas
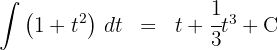
4Voltamos para a variável inicial
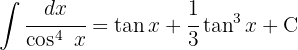
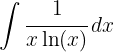
1Realizamos a mudança de variável e calculamos o diferencial:
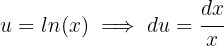
2Substituímos na integral e simplificamos
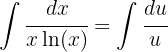
3Resolvemos a integral obtida:
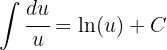
4Voltamos para a variável inicial:

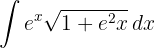
1Realizamos a mudança de variável e calculamos o diferencial:
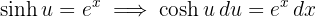
2Substituímos na integral e simplificamos, utilizando:
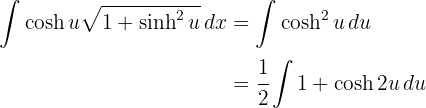
3Resolvemos a integral obtida:
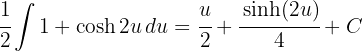
4Voltamos para a variável inicial:


1Realizamos a mudança de variável e calculamos o diferencial:
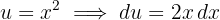
2Substituímos na integral e simplificamos, utilizando:
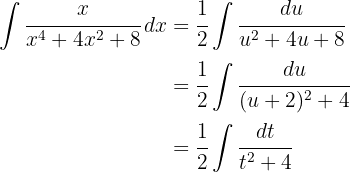
3Resolvemos a integral obtida:
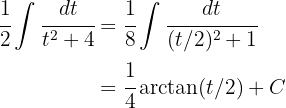
4Voltamos para a variável inicial usando 

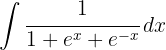
1Realizamos a mudança de variável e calculamos o diferencial:
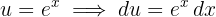
2Substituímos na integral e simplificamos, utilizando:
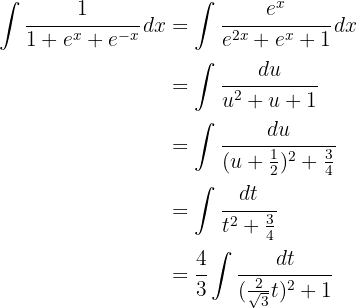
3Resolvemos a integral obtida:
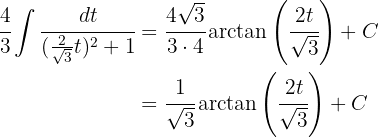
4Voltamos para a variável inicial, usando 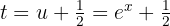
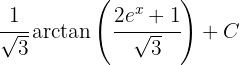

1Realizamos a mudança de variável e calculamos o diferencial:
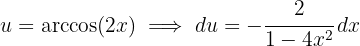
2Substituímos na integral e simplificamos, utilizando:
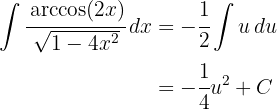
3Voltamos para a variável inicial, usando 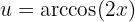
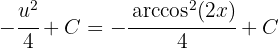
Resumir com IA:


