Bem-vindo à nossa página de exercícios resolvidos de Integrais! Se você é um ou uma estudante, já deve saber que o cálculo integral é uma das áreas mais importantes da matemática, com inúmeras aplicações em outras áreas do conhecimento.
Neste artigo, você encontrará explicações com passo a passo, exemplos resolvidos e dicas úteis para resolver integrais de maneira eficaz, utilizando diferentes técnicas de integração. Se você está buscando aprimorar suas habilidades matemáticas ou apenas precisando de ajuda com um problema específico, você veio ao lugar certo!
Te convidamos a resolver as integrais abaixo por conta própria e, em seguida, verificar suas respostas com as soluções exibidas que o Superprof tem para você. Chega junto e bora!
Resolver as integrais abaixo
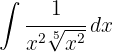
Para resolver a integral, elevamos o denominador e simplificamos as potências, em seguida, aplicamos a integral imediata de potências.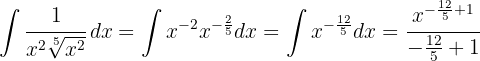
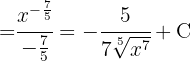
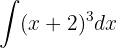
Para resolver a integral, fazemos a mudança de variável.  e então, aplicamos a integral imediata de potências.
e então, aplicamos a integral imediata de potências.


Para resolver a integral, fazemos a mudança de variável. 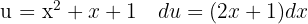 , e então, aplicamos a integral imediata de potências.
, e então, aplicamos a integral imediata de potências.
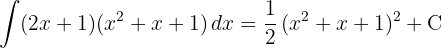

Para resolver a integral, fazemos a substituição de variável.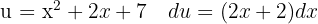 , e então, aplicamos a integral imediata de potências.
, e então, aplicamos a integral imediata de potências.

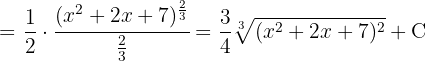
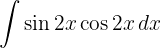
Para resolver a integral, fazemos a substituição de variável.  ,e então, aplicamos a integral imediata de potências.
,e então, aplicamos a integral imediata de potências.
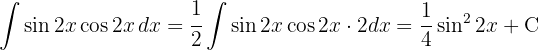
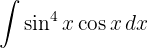
Para resolver a integral, fazemos a mudança de variável.  , e então, aplicamos a integral imediata de potências.
, e então, aplicamos a integral imediata de potências.
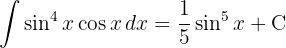
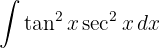
Para resolver a integral, fazemos a substituição de variável.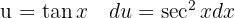 , e então, aplicamos a integral imediata de potências.
, e então, aplicamos a integral imediata de potências. 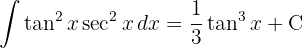
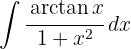
Para resolver a integral, fazemos a substituição de variável. 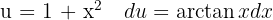 , e então aplicamos a integral imediata de potências.
, e então aplicamos a integral imediata de potências.
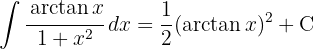
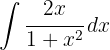
Para resolver a integral, fazemos a substituição de variável.  , e então aplicamos a integral imediata de potências.
, e então aplicamos a integral imediata de potências.  .
.
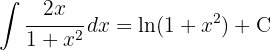
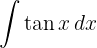
Para resolver a integral, utilizamos a definição da tangente em termos de seno e cosseno, e então aplicamos a integral imediata de potências.  .
.

Para resolver a integral, realizamos uma mudança de variável.  , e então aplicamos a integral imediata de potências.
, e então aplicamos a integral imediata de potências.
 .
.
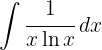
Para resolver a integral, realizamos uma mudança de variável. 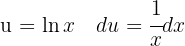 , e então aplicamos a integral imediata de potências.
, e então aplicamos a integral imediata de potências.
 .
.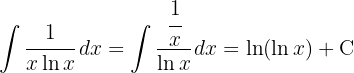

Para resolver a integral, realizamos uma mudança de variável.  , e então aplicamos a integral imediata de potências.
, e então aplicamos a integral imediata de potências.  .
.
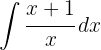
Para resolver a integral, separamos a integral e então aplicamos a integral imediata de potências.  .
.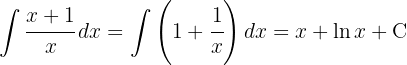
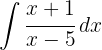
Para resolver a integral, adicionamos um zero para poder separá-la em duas integrais e então aplicamos a integral imediata de potências.  .
.

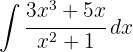
Para resolver a integral, começamos fazendo uma divisão sintética para poder separá-la em duas integrais, e então aplicamos a integral imediata de potências.  , com uma troca de variável
, com uma troca de variável  .
.
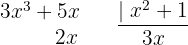
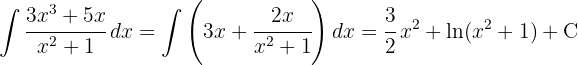
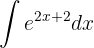
Para resolver a integral, realizamos uma mudança de variável.  e então aplicamos a integral imediata de potências.
e então aplicamos a integral imediata de potências.  .
.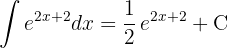

Para resolver a integral, fazemos a integral imediata 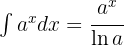 .
.
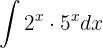
Para resolver a integral, fazemos a integral imediata 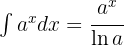 .
.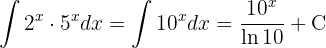
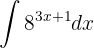
Para resolver a integral, realizamos uma mudança de variável 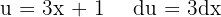 e então aplicamos a integral imediata
e então aplicamos a integral imediata 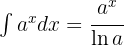 .
.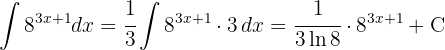
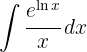
Para resolver a integral, realizamos uma mudança de variável. 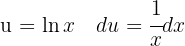 e então aplicamos a integral imediata de potências.
e então aplicamos a integral imediata de potências.  .
.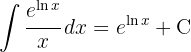 .
.

Para resolver a integral, realizamos uma mudança de variável.  e então aplicamos a integral imediata de potências.
e então aplicamos a integral imediata de potências.  .
.

Para resolver a integral, realizamos uma mudança de variável. 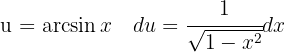 e então aplicamos a integral imediata de potências.
e então aplicamos a integral imediata de potências.  .
.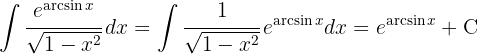
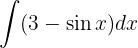
Começamos separando a integral e aplicando as respectivas integrais imediatas. 


Começamos fazendo uma mudança de variável 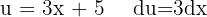 e aplicar a integral imediata
e aplicar a integral imediata 


Começamos fazendo uma mudança de variável 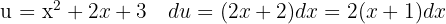 e aplicar a integral imediata
e aplicar a integral imediata 
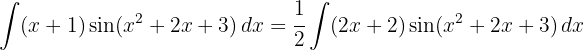

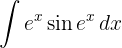
Começamos fazendo uma mudança de variável 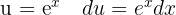 e aplicar a integral imediata
e aplicar a integral imediata 


Começamos fazendo uma mudança de variável  e aplicar a integral imediata
e aplicar a integral imediata 


Começamos por utilizar a identidade.  , separar a integral e aplicar a integral imediata
, separar a integral e aplicar a integral imediata  , con un cambio de variable
, con un cambio de variable  .
.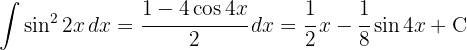
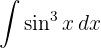
Vamos começar com separando e seno e utilizando a identidade trigonométrica. 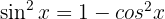 , aplicando a integral imediata
, aplicando a integral imediata  e uma substituição de variável
e uma substituição de variável 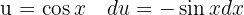
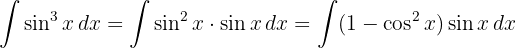
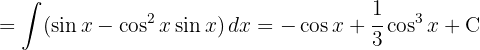
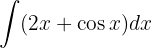
Vamos começar separando a integral e aplicar a integral imediata 

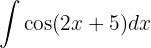
Começamos fazendo uma mudança de variável 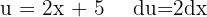 e aplicar a integral imediata
e aplicar a integral imediata 
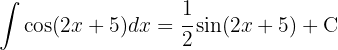
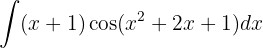
Começamos fazendo uma troca de variável 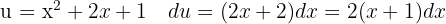 e aplicar a integral imediata
e aplicar a integral imediata

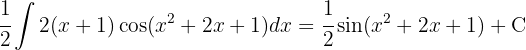

Começamos fazendo uma troca de variável  e aplicar a integral imediata
e aplicar a integral imediata 


Começamos utilizando a identidade trigonométrica 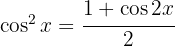 , separar a integral e aplicar a integral imediata
, separar a integral e aplicar a integral imediata  , com uma troca de variável
, com uma troca de variável 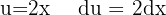

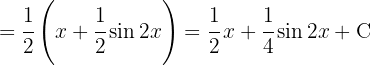

Vamos começar utilizando a identidade trigonométrica 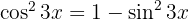 , separando a integral, aplicar a integral imediata
, separando a integral, aplicar a integral imediata  , e uma troca de variável
, e uma troca de variável 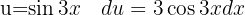


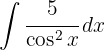
Começamos utilizando a identidade trigonométrica 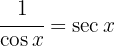 e aplicar a integral imediata
e aplicar a integral imediata 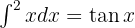 }
}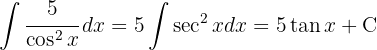
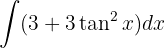
Começamos utilizando a identidade trigonométrica  e aplicamos a integral imediata
e aplicamos a integral imediata 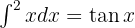 }
} 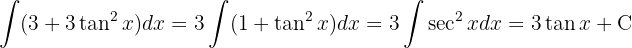

Vamos começar fazendo uma troca de variável  e aplicar a integral imediata
e aplicar a integral imediata 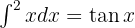 }
} 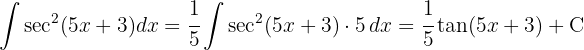

Começamos separando a secante e utilizando a identidade trigonométrica  , aplicar a integral imediata
, aplicar a integral imediata 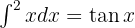 e uma troca de variável
e uma troca de variável 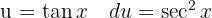
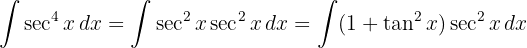

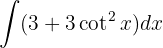
Começamos utilizando a identidade trigonométrica 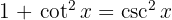 e aplicar a integral imediata
e aplicar a integral imediata 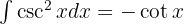
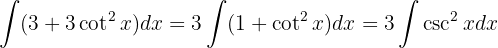
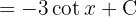

Começamos adicionando um zero e utilizando a identidade trigonométrica  , separamos a integral e aplicamos a integral imediata
, separamos a integral e aplicamos a integral imediata 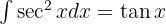

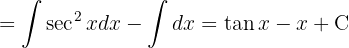
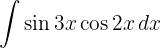
Para resolver a integral, vamos encontrar os valores de A e B que satisfaçam a seguinte identidade

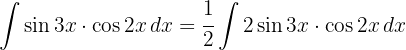
Aplicamos a identidade anterior, seguida por uma mudança de variável. 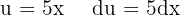 e aplicamos a integral
e aplicamos a integral 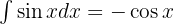
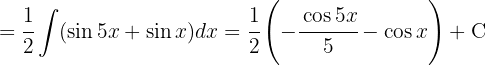
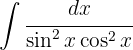
Para resolver a integral, utilizamos a identidade trigonométrica.  , separamos a integral e simplificamos.
, separamos a integral e simplificamos.

Agora, vamos usar as definições 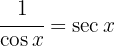 y
y 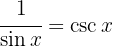 e, finalmente, as integrais imediatas.
e, finalmente, as integrais imediatas.  y
y 
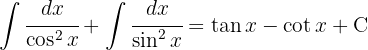
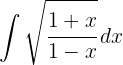
Para resolver a integral a seguir, multiplicamos o numerador e o denominador por  , e então, separamos a integral
, e então, separamos a integral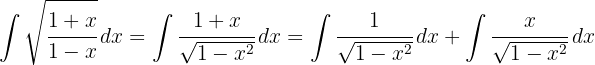
Aplicamos a integral  com a mudança de variável
com a mudança de variável 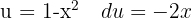
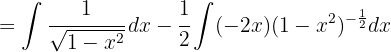


Para resolver a integral a seguir, multiplicamos o numerador e o denominador por 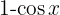 , colocamos o binômio ao quadrado, utilizando a identidade
, colocamos o binômio ao quadrado, utilizando a identidade 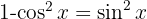 e, então, separamos a integral
e, então, separamos a integral
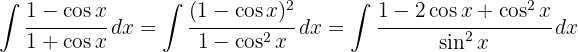
Agora usamos as definições 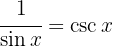 , a integral imediata
, a integral imediata  , uma mudança de variável
, uma mudança de variável 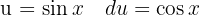 e adicionamos um zero para poder utilizar a identidade.
e adicionamos um zero para poder utilizar a identidade. 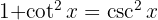 e, por fim, a integral
e, por fim, a integral 


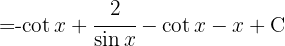

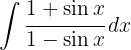
Para resolver a integral a seguir, multiplicamos o numerador e o denominador por 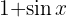 , desenvolvemos o binômio ao quadrado, utilizando a identidade
, desenvolvemos o binômio ao quadrado, utilizando a identidade 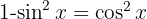 e, depois separamos a integral
e, depois separamos a integral
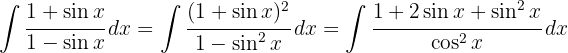

Agora, utilizamos as definições 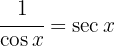 , a integral imediata
, a integral imediata 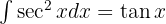 , uma mudança de variável
, uma mudança de variável 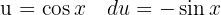 e adicionamos um zero para poder utilizar a identidade
e adicionamos um zero para poder utilizar a identidade 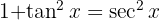
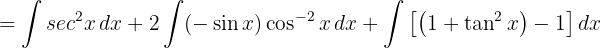
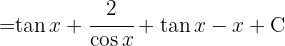
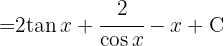

Para resolver a integral a seguir, buscamos completar os quadrados para ter uma integral da forma 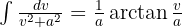 , onde
, onde 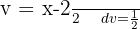 .
.
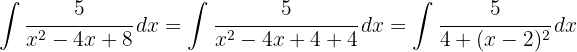
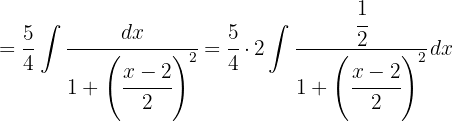
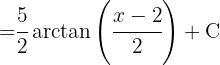

Começamos separando a integral; por um lado, temos uma mudança de variável  , por outro lado, buscamos ter uma integral da forma.
, por outro lado, buscamos ter uma integral da forma. 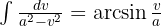 , onde
, onde 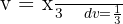 .
.
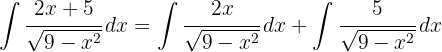
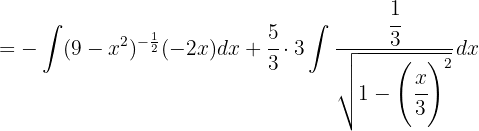


Estamos procurando obter uma integral na forma 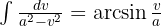 , onde
, onde  .
.
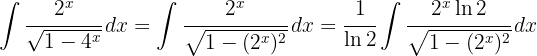
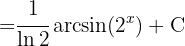
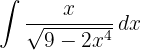
Estamos procurando obter uma integral na forma 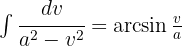 , então, no denominador, podemos fazer a seguinte mudança:
, então, no denominador, podemos fazer a seguinte mudança:

onde 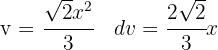 .
.

Resumir com IA:


