Temas
Vamos lembrar que uma inequação é uma desigualdade algébrica, ou seja, uma expressão algébrica separada pelos sinais 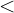 (menor que),
(menor que), 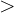 (maior que),
(maior que),  (menor ou igual a) ou
(menor ou igual a) ou  (maior ou igual a).
(maior ou igual a).
Neste caso, vamos analisar as inequações do segundo grau, também chamadas de inequações quadráticas, da forma: 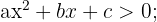 em que
em que  e
e  são números reais e
são números reais e 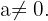

Procedimento para a resolução de uma inequação do 2º grau
Vamos resolver a inequação do segundo grau  seguindo a seguinte sequência de passos:
seguindo a seguinte sequência de passos:
1Igualar o primeiro membro a zero e calcular as raízes da equação do segundo grau associada
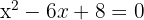
Neste caso, o método mais direto é a fatoração:
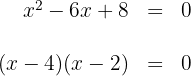
Igualamos cada fator a zero e obtemos as raízes:
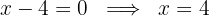

Observação: Esse primeiro passo, obter as raízes da equação do segundo grau associada, também é conhecido como encontrar os valores críticos da inequação.
2Representar esses valores na reta real
A reta real fica dividida em três intervalos a partir dos valores  e
e  :
: 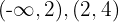 e
e  .
.
Escolhe-se um ponto de cada intervalo e substitui-se na inequação para verificar o sinal da expressão em cada um. Por exemplo, podemos usar a tríade de valores: 


Observação: Caso a inequação estivesse representada pelos sinais “menor ou igual a” ou “maior ou igual a”, os intervalos das extremidades deveriam ser 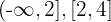 e
e 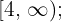 ou seja, os extremos dos intervalos deveriam ser incluídos, tornando-se intervalos fechados ou semiabertos.
ou seja, os extremos dos intervalos deveriam ser incluídos, tornando-se intervalos fechados ou semiabertos.
3Análise do sinal dos valores e da expressão quadrática
A solução é formada pelos intervalos em que a expressão possui o mesmo sinal indicado na inequação. Neste caso, a expressão deve ser positiva, pois a inequação é do tipo “maior que zero”.

Portanto, a solução da inequação do segundo grau é o conjunto 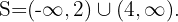
Casos especiais para resolver inequações de 2º grau
Uma inequação formada por um binômio ao quadrado
A seguir, analisaremos a inequação 
Aplicando o método da fatoração, temos:
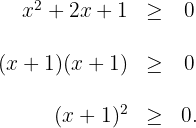
Como qualquer número real elevado ao quadrado é sempre maior ou igual a zero, sempre que uma inequação for positiva e associada ao sinal  e se tratar de um binômio ao quadrado, sua solução será todo o conjunto dos números reais:
e se tratar de um binômio ao quadrado, sua solução será todo o conjunto dos números reais:  .
.
Caso a inequação esteja associada a outros sinais de desigualdade, as soluções seguem a tabela abaixo:

Uma inequação sem pontos críticos
Vamos analisar agora a inequação: 
Sua equação de 2º grau associada é 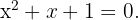
Uma maneira de saber quantas soluções tem uma equação de 2º grau é calcular o discriminante 
1 Se esse valor for positivo, a equação terá duas raízes reais
2 Se esse valor for zero, terá apenas uma raiz real
3 Se esse valor for negativo, não terá raízes reais.
Calculamos o discriminante usando os coeficientes 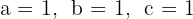
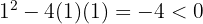
Portanto, a inequação não tem pontos críticos e, por isso, a reta numérica não é dividida.
Dessa forma, a inequação pode ter como solução todos os números reais ou nenhum número real. Se o sinal do termo quadrático for diferente do sinal da desigualdade, a inequação não tem solução.

Exercícios de inequações de 2º grau ou quadráticas
x^2-1<0
1 Obtenha os valores críticos da inequação.
Para isso, vamos igualar a zero e fatorar:
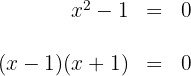
Igualando os fatores a zero, vamos obter as raízes 
2 Represente os valores críticos na reta numérica.
Como as raízes são 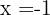 e
e  , a reta real é dividida nos intervalos
, a reta real é dividida nos intervalos 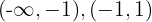 e
e 
Considerando os valores 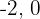 e
e 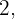 e fazendo a substituição na inequação:
e fazendo a substituição na inequação:
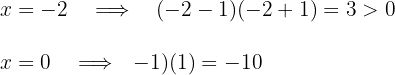

Como a expressão do 2º grau é negativa, a solução é o intervalo 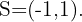
7-x^2<0
1 Obtenha os valores críticos da inequação
Para isso, igualamos a zero e fazemos a fatoração.
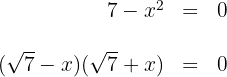
Igualando os fatores a zero, vamos obter as raízes 
2 Represente os valores críticos na reta numérica.
Como as raízes são 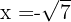 e
e 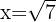 , a reta real é dividida nos intervalos
, a reta real é dividida nos intervalos 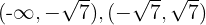 e
e 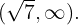
Considerando os valores 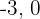 e
e  e fazendo a substituição na inequação:
e fazendo a substituição na inequação:
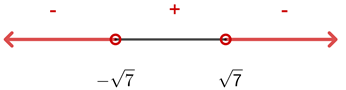
Como a expressão do 2º grau é negativa, a solução é o intervalo 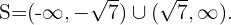
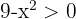
1 Obtenha os valores críticos da inequação.
Para isso, vamos igualar a zero e fatorar:
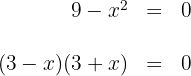
Igualando os fatores a zero, obtêm-se as raízes 
2 Represente os valores críticos na reta numérica.
Como as raízes são 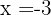 e
e  , a reta real é dividida nos intervalos
, a reta real é dividida nos intervalos 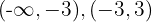 e
e 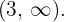
Considerando os valores 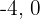 e
e  e fazendo a substituição na inequação:
e fazendo a substituição na inequação:

Como a expressão do 2º grau é positiva, a solução é o intervalo 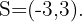
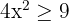
1 Obtenha os valores críticos da inequação.
Para isso, vamos igualar a zero e fatorar:
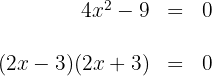
Igualando os fatores a zero, obtêm-se as raízes 
2 Represente os valores críticos na reta numérica.
Como as raízes são 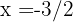 e
e 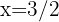 , a reta real é dividida nos intervalos
, a reta real é dividida nos intervalos 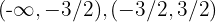 e
e 
Considerando os valores 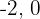 y
y 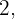 e fazendo a substituição na inequação.
e fazendo a substituição na inequação.
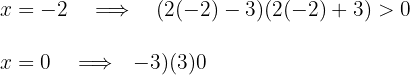
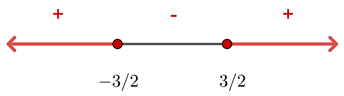
Como a expressão do 2º grau é negativa, a solução é o intervalo 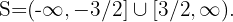
- x^2 < 4
1 Obtenha os valores críticos da inequação.
Como não é possível fatorar como o produto de dois binômios, vamos calcular o valor do discriminante:
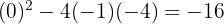
2 Como o discriminante é negativo, a inequação ou não possui soluções, ou suas soluções são todos os números reais.
Como o sinal do termo quadrático coincide com o da desigualdade (negativo – menor que), a solução da inequação é o conjunto dos números reais:
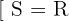
x^2-4x+4 < 0
1 Obtenha os valores críticos da inequação.
Para isso, igualamos a zero e fatoramos:
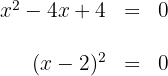
Igualando o fator a zero, obtém-se 
2 Represente os valores críticos na reta numérica.
Como la raiz é 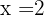 a reta é dividida nos intervalos
a reta é dividida nos intervalos 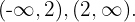
Considerando os valores  e
e  e substituindo-os na inequação:
e substituindo-os na inequação:
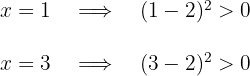
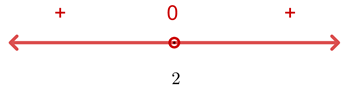
Como a expressão do 2º grau é sempre positiva ou igual a zero, a inequação não possui solução.
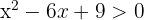
1 Obtenha os valores críticos da inequação.
Para isso, igualamos a zero e fatoramos:

Igualando o fator a zero, vamos obter 
2Represente os valores críticos na reta numérica.
Como la raiz é 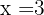 reta é dividida nos intervalos
reta é dividida nos intervalos 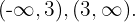
Considerando os valores  e
e  e substituindo-os na inequação:
e substituindo-os na inequação:
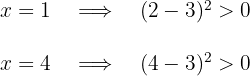
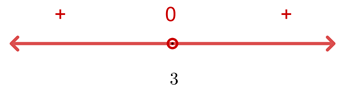
Como a expressão do 2º grau é sempre positiva ou igual a zero, a inequação tem como solução: 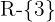
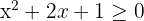
1 Obtenha os valores críticos da inequação.
Para isso, igualamos a zero e fatoramos:
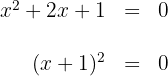
Igualando o fator a zero, obtém-se 
2 Represente os valores críticos na reta numérica
Como a raiz é 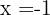 a reta é dividida nos intervalos
a reta é dividida nos intervalos 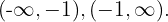
Considerando os valores  e
e 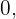 e substituindo-os na inequação:
e substituindo-os na inequação:
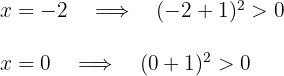
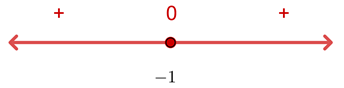
Como a expressão do 2º grau é sempre positiva ou igual a zero, a inequação tem como solução o conjunto dos números reais: 
 7x^2+21x-28<0[/latex]
7x^2+21x-28<0[/latex]
1 Obtenha os valores críticos da inequação.
Para isso, igualamos a zero e fatoramos:

Igualando o fator a zero, obtemos as raízes 
2 Represente os valores críticos na reta numérica.
Como a raiz é 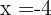 e
e  , a reta real é dividida nos intervalos
, a reta real é dividida nos intervalos 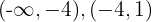 e
e 
Considerando os valores 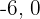 e
e  e substituindo-os na inequação:
e substituindo-os na inequação:
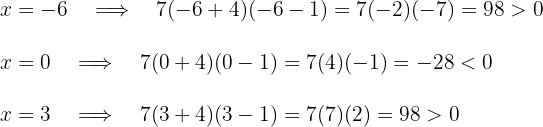

Como a expressão do 2º grau é negativa, a solução é o intervalo 
 -x^2+4x-7<0[/latex]
-x^2+4x-7<0[/latex]
1 Determine os valores críticos da inequação.
Como não é possível fatorar como o produto de dois binômios, calculamos o valor do discriminante:
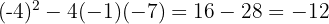
2 Como o discriminante é negativo, a inequação ou não possui solução, ou a solução é o conjunto dos números reais.
Como o sinal do termo do 2º grau coincide com o da desigualdade (negativo – “menor que”), a solução da inequação é o conjunto dos números reais: 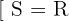
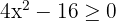
1 Determine os valores críticos da inequação.
Para isso, igualamos a zero e fatoramos:
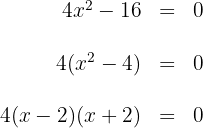
Igualando os fatores a zero, obtêm-se as raízes  . Essas raízes são soluções da inequação (já que, ao substituí-las, a desigualdade satisfazem em uma igualdade verdadeira).
. Essas raízes são soluções da inequação (já que, ao substituí-las, a desigualdade satisfazem em uma igualdade verdadeira).
2 Represente os valores críticos de uma reta numérica.
Como as raízes são 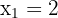 e
e 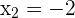 , a reta real é dividida nos intervalos
, a reta real é dividida nos intervalos  e
e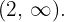
Considerando os valores 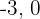 e
e  e substituindo-os na inequação:
e substituindo-os na inequação:
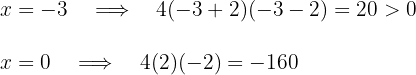

Como a expressão do 2º grau é positiva nos intervalos externos, a solução da inequação é a união dos dois intervalos: 
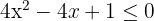
1 Obter os valores críticos da inequação.
Para isso, igualamos a zero e fatoramos:

Igualando o fator a zero, obtém-se a raiz 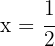
2 Como o binômio ao quadrado é sempre não negativo e o sinal da inequação é "menor ou igual que", a inequação possui uma única solução: 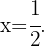
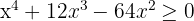
1 Obter os valores críticos da inequação.
Para isso, igualamos a zero e fatoramos:
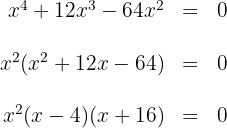
Igualando os fatores a zero, obtêm-se as raízes 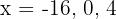 . Essas raízes são soluções da inequação (já que, ao substituí-las, a desigualdade se transforma em uma igualdade verdadeira).
. Essas raízes são soluções da inequação (já que, ao substituí-las, a desigualdade se transforma em uma igualdade verdadeira).
2 Representar os valores críticos na reta numérica.
Como as raízes são  e
e  , a reta real é dividida nos seguintes intervalos:
, a reta real é dividida nos seguintes intervalos:  e
e 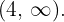
Considerando os valores 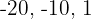 e
e  e substituindo-os na inequação:
e substituindo-os na inequação:
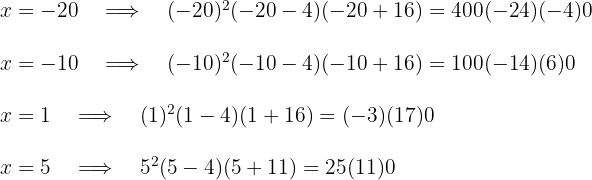

Como a expressão é positiva nos intervalos extremos, a solução é a união dos intervalos 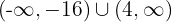 e incluindo, também, os valores críticos que satisfazem a inequação.
e incluindo, também, os valores críticos que satisfazem a inequação.
Assim, a solução final é:
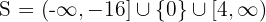
 x^4-25x^2+144< 0 [/latex]
x^4-25x^2+144< 0 [/latex]
1 Obtenha os valores críticos da inequação.
Para isso, igualamos a zero e fatoramos:
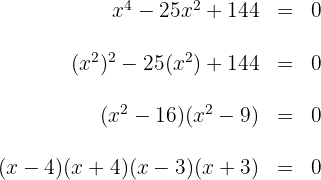
Igualando os fatores a zero, obtêm-se as raízes 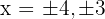 .
.
2 Represente os valores críticos na reta numérica.
Como as raízes são 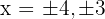 , a reta real é dividida nos seguintes intervalos:
, a reta real é dividida nos seguintes intervalos: 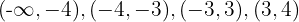 e
e 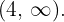
Considerando os valores  e
e  fazemos a substituição na inequação.
fazemos a substituição na inequação.
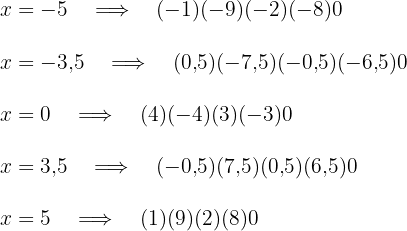

Como a expressão do 2º grau é negativa, a solução é a união dos intervalos 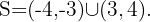

1 Obter os valores críticos da inequação.
Para isso, igualamos a zero e fatoramos:

Como o binômio 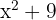 é sempre maior que zero para qualquer valor de
é sempre maior que zero para qualquer valor de  , apenas os binômios lineares são considerados para calcular os valores críticos. Portanto,
, apenas os binômios lineares são considerados para calcular os valores críticos. Portanto,  são as raízes buscadas. Essas raízes são soluções (já que, ao substituí-las na inequação, a igualdade é satisfeita).
são as raízes buscadas. Essas raízes são soluções (já que, ao substituí-las na inequação, a igualdade é satisfeita).
2 Represente os valores críticos na reta numérica.
Como as raízes são;
 , la recta real se divide en los intervalos
, la recta real se divide en los intervalos 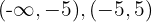 e
e 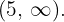
Considerando os valores  e
e  , e fazemos a substituição na inequação.
, e fazemos a substituição na inequação.


Como a expressão é positiva ou igual a zero nos intervalos extremos e nos pontos críticos, a solução é a união desses intervalos com os valores críticos. Assim, a solução é:
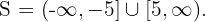
Resumir com IA:












