As equações logarítmicas são fundamentais na matemática porque ajudam a resolver problemas em várias áreas, como ciência e economia. De um jeito simples, um logaritmo responde à pergunta: "A que número precisamos elevar uma base para chegar a um certo valor?" Essa propriedade transforma multiplicações em somas, o que facilita bastante na hora de resolver equações mais complicadas.
Agora, resolva as equações logarítmicas a seguir!
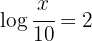
a. Aplicamos a propriedade do logaritmo de um quociente:
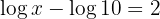
b. Levando em conta que 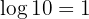
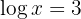
c. Tendo em consideração a definição do logaritmo e que se trata de um logaritmo decimal:
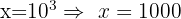
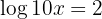
a. Aplicamos a propriedade do logaritmo do produto:
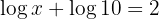
b. Considerando que 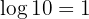
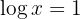
c. Tendo em conta a definição do logaritmo e que se trata de um logaritmo decimal:
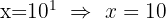
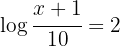
a. Aplicamos a propriedade do logaritmo do quociente:
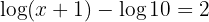
b. Sabendo que 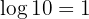
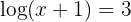
c. Considerando definição do logaritmo e que se trata de um logaritmo decimal:
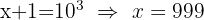
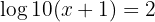
a. Aplicamos a propriedade do logaritmo do produto:
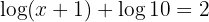
b. Tendo em conta que 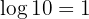
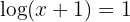
c. Tendo em consideração a definição do logaritmo e que se trata de um logaritmo decimal:
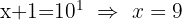
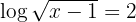
a. No lado esquerdo da equação, escrevemos a raiz como potência fracionária e aplicamos a propriedade do logaritmo de uma potência:
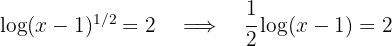
b. Isolamos a variável:
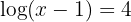
c. Levando em conta a definição de logaritmo e que se trata de um logaritmo decimal:
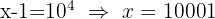
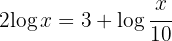
a. Aplicamos a propriedade do logaritmo de um quociente, no lado direito da equação:
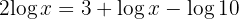
b. Subtraímos  dos dois lados e, levando em conta que
dos dois lados e, levando em conta que 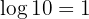 , temos:
, temos:
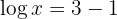
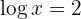
c. Considerando a definição de logaritmo e que se trata de um logaritmo decimal:
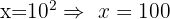
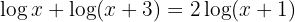
a. No lado esquerdo da equação, aplicamos a propriedade da soma de logaritmos:
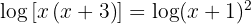
b. Considerando que estamos igualando os argumentos, temos:

c. Resolvemos a equação e verificamos a solução:
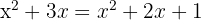


a. Aplicamos a propriedade do logaritmo de uma potência em ambos os membros:
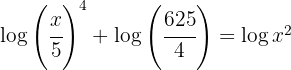
b. Aplicamos a propriedade do logaritmo de um produto:
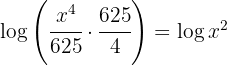
c. Fazemos a operação do lado esquerdo da equação:

d. Igualamos os argumentos para remover logaritmos:
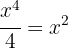
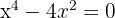
e. Resolvemos a equação:
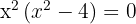
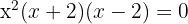
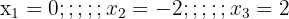
f. Nem  nem
nem  são soluções, pois ao substituí-los na equação obtemos logaritmo de 0 e logaritmo de um número negativo, que não são definidos.
são soluções, pois ao substituí-los na equação obtemos logaritmo de 0 e logaritmo de um número negativo, que não são definidos.
Assim, a única solução é  .
.
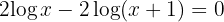
a. Passamos 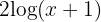 para o lado direito e aplicamos a propriedade da potência em ambos os membros:
para o lado direito e aplicamos a propriedade da potência em ambos os membros:
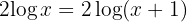

b. Igualamos os argumentos e encontramos os valores de 
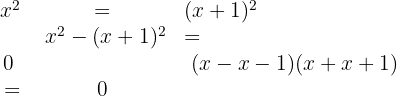
c. Resolvendo o primeiro fator obtemos 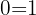 , o que é uma inconsistência e significa que a equação não tem solução. Resolvendo o segundo fator, temos
, o que é uma inconsistência e significa que a equação não tem solução. Resolvendo o segundo fator, temos 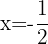 , mas
, mas  não está definido.
não está definido.
Portanto, a equação não tem solução.

a. Eliminamos os denominadores e realizamos uma mudança de variável:
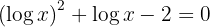
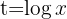
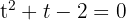
b. Resolvendo a equação:
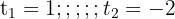
c. Desfazemos a mudança de variável e aplicamos a definição de logaritmo:
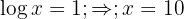
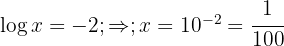

a. Passamos o segundo termo para o lado direito e aplicamos a propriedade do logaritmo de uma potência:
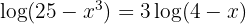

b. Igualamos os argumentos e desenvolvemos as operações:
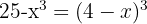
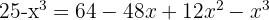
c. Resolvemos a equação aplicando a fórmula geral:

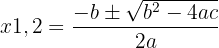
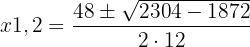
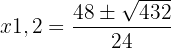

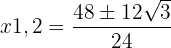
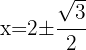

a. Multiplicamos ambos os membros por 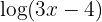
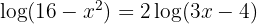
b. Aplicamos a propriedade do logaritmo de uma potência e igualamos os argumentos:

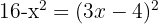
c. Resolvemos a equação.
 não é solução, pois levaria ao logaritmo de um número negativo no denominador ao substituir na equação.
não é solução, pois levaria ao logaritmo de um número negativo no denominador ao substituir na equação.

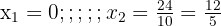
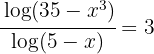
a. Eliminamos denominadores:
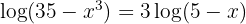
b. Vamos aplicar a propriedade do logaritmo de uma potência e posteriormente, igualar os argumentos:

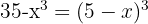
c. Realizamos as operações e resolvemos a equação do 2º grau:

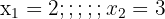
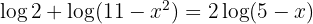
a. Do lado esquerdo, aplicamos a propriedade do logaritmo de um produto e, no segundo, a propriedade do logaritmo de uma potência.
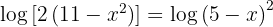
b. Considerando que precisamos igualar os argumentos, temos que:
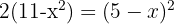
c. Resolvemos a equação e verificamos se não obtemos um logaritmo nulo ou negativo
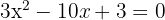


a. Multiplicamos ambos os membros por 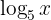 e passamos tudo para o lado esquerdo:
e passamos tudo para o lado esquerdo:
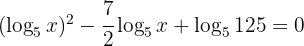
b. Considerando que  e eliminando denominadores:
e eliminando denominadores:
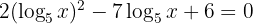
c. Realizamos uma mudança de variável:
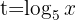
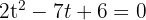
d. Resolvemos a equação:

e. Desfazemos a mudança de variável
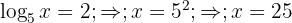
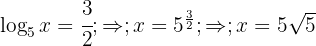
Resumir com IA:


