Exercícios de Equações Exponenciais

1 Como o número 4   pode ser escrito como 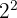, podemos reescrever a equação da seguinte forma:

2Agora que temos a mesma base em ambos os lados da equação, podemos igualar os expoentes:

3 Resolvemos a equação do 1º grau que surgiu:

1 Transformamos as raízes em potências com expoente fracionário e podemos igualar os expoentes:

2 Resolvemos a nova equação:

1 Reescrevemos  como e igualamos os exponentes

2 Resolvemos a nova equação

1 Reescrevemos a raiz na forma de potência com exponente fracionário e  é decomposto em fatores.

1Transformamos a fração do lado direito

2 Igualamos exponentes e resolvemos a nova equação:

1Transformamos a raiz em uma potência com expoente fracionário.

2 Resolvemos a equação resultante

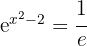
1Transformamos a fração do lado direito

2 Igualamos exponentes e resolvemos a equação resultante

1Reescrevemos a fração do lado direito e expressamos a raiz quadrada como expoente fracionário:

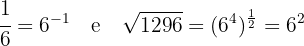
2 Igualamos as potências e resolvemos a equação resultante:

1 Decompomos os números  e e igualamos os expoentes:

2 Podemos simplificar a equação resultante para então, ser resolvida:

1 Passamos o segundo termo para o lado direito, decompomos o número e igualamos os exponentes:

2 Resolvemos a equação irracional resultante:

Como temos bases diferentes, aplicamos logaritmos em ambos os lados:

2 Aplicamos a propriedade do logaritmo de uma potência no primeiro membro:

3 Passamos para o outro lado e resolvemos a equação:

1 Podemos reescrever a equação como:

2 Passamos para primeiro membro e para o segundo membro:

3 Aplicamos logaritmo nos dois membros:

4 Aplicamos a propriedade do logaritmo de uma potência no primeiro membro e resolvemos a equação resultante:

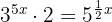
1 Podemos reescrever a equação como:

2 Passamos para o primeiro membro e  para o segundo membro:

3Aplicamos logaritmo em ambos os membros

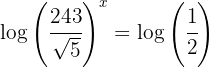
4 Aplicamos a propriedade do logaritmo de uma potência no primeiro membro e resolvemos a equação resultante:

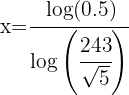
1 Aplicamos logaritmo em ambos os membros

2 Aplicamos a propriedade do logaritmo de uma potência no primeiro membro e resolvemos a equação resultante:

1 Aplicamos logaritmo em ambos os membros e aplicamos a propriedade do logaritmo do produto no primeiro membro

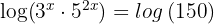
2 Aplicamos a propriedade do logaritmo da potência e colocamos o fator comum em evidência:

3 Isolamos a incógnita e resolvemos as operações com os logaritmos:

1 Aplicamos a propriedade da potência no produto e no quociente, para eliminar a soma ou subtração dos expoentes

2 Colocamos 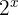como fator comum

3 Isolamos 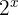e expressamos ambos os membros com base

4 Igualamos os exponentes

1 Aplicamos a propriedade da potência no produto e no quociente, para eliminar  subtração dos expoentes:

2 Fazemos a substituição de variável e  substituimos na equação:

3 Ao multiplicar ambos os membros da equação por passar todos os termos para o primeiro membro, obtemos:

4 Ao resolver a equação do segundo grau, obtemos:

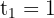
5 Substituimos os valores de em

   ...

  ...

6  A equação não tem  solução, pois uma potência com base positiva nunca resulta em número negativo. Assim, resolvemos apenas a equação

1 Aplicamos as propriedades das potências no produto ou quociente, para eliminar as somas ou subtrações nos expoentes:

2 Fazemos a substituição da variável  e substituímos na equação:

3 Multiplicamos os dois membros por e resolvemos a equação resultante:

Não tem solução

1 Decompomos em fatores e aplicamos as propriedades do produto e do quociente de potências para eliminar as somas e subtrações nos expoentes:

2 Fazemos a substituição da variável e resolvemos a equação resultante:

3 Retornamos à variável original e verificamos se as soluções são válidas:

Não tem solução

1 Decompomos em fatores  e 

2 Fazemos a substituição da variável e resolvemos a equação resultante:

3 Desfazemos a substituição da variável apenas com a solução positiva:

4 Como não podemos igualar os expoentes, aplicamos logaritmo em ambos os membros e, no primeiro membro, usamos a propriedade da potência:

5 Isolamos a variável

6 Para a solução negativa da equação quadrática, não há solução para a equação exponencial, pois ao aplicar logaritmo no segundo membro, teríamos o logaritmo de um número negativo, o que não é possível.

 Não tem solução

1 Eliminamos os expoentes negativos fazendo o inverso:

2 Eliminamos os denominadores multiplicando por

3 Fazemos a substituição da variável e resolvemos a equação resultante:

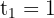
4 Retornamos à variável original e resolvemos 

1 Fazemos a substituição da variável

2 Resolvemos a equação e desfazemos a substituição da variável:

Não tem solução

1 Aplicamos a fórmula da soma dos  termos de uma progressão geométrica:

2 Isolamos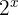

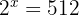
3 Reescrevemos o como e igualamos as potências

1 Aplicamos la fórmula de soma de termos de uma progressão geométrica:

2 Colocamos os termos com denominador comum:

3 Eliminamos os denominadores e resolvemos a equação resultante:

1 Elevamos ambos os lados da equação ao cubo para manter a igualdade:

2 Utilizamos as propriedades dos expoentes e reescrevemos a equação.

Sabemos que:

3 Novamente, utilizamos as propriedades dos expoentes e reescrevemos a equação:

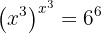
4 Portanto, temos que:

5 Finalmente, temos que: