Seja bem-vindo e bem-vinda aos exercícios de equações da reta no plano! Nesta série de exercícios, mergulharemos no emocionante mundo da geometria analítica e aprenderemos a representar e compreender as retas no plano cartesiano.
A equação da reta é uma ferramenta fundamental para descrever a relação linear entre variáveis e entender como elas se comportam em função das mudanças em uma ou mais dimensões. Através desses exercícios, exploraremos diferentes formas de expressar a equação de uma reta, como a forma contínua, a forma ponto-pendente ou até mesmo a forma geral.
A equação da reta é uma ferramenta fundamental para descrever a relação linear entre variáveis e entender como elas se comportam em função das mudanças em uma ou mais dimensões. Através desses exercícios, exploraremos diferentes formas de expressar a equação de uma reta, como a forma contínua, a forma ponto-pendente ou até mesmo a forma geral.

Distância entre pontos e retas
Calcule a distância do ponto  á reta
á reta  da equação
da equação 
Para uma equação da  expressa em sua forma ordinária
expressa em sua forma ordinária  e um ponto
e um ponto  , é possível calcular sua distância através da seguinte fórmula:
, é possível calcular sua distância através da seguinte fórmula:

Neste caso, os coeficientes e as coordenadas do ponto são determinados da seguinte maneira:





Fazendo a substituição destas variáveis na fórmula anterior, vamos obter

Ou seja, a distância entre  e
e  é igual a
é igual a

Encontre a distância entre  e
e 
Considerando as retas  y
y  , acontece um e apenas um dos cenários seguintes: ou eles são paralelos ou têm algum ponto em comum.
, acontece um e apenas um dos cenários seguintes: ou eles são paralelos ou têm algum ponto em comum.
Se forem retas paralelas, elas são distintas ou coincidem. Ou seja, são distintas ou são a mesma reta. É por isso que, antes de calcular a distância entre duas retas, é necessário calcular a inclinação para determinar em qual caso estamos.
Se tiverem a mesma inclinação, serão retas paralelas; caso contrário, se cruzarão em algum ponto.
Para uma equação da reta  expressa em sua forma ordinária
expressa em sua forma ordinária  a inclinação delas é determinada pela expressão.
a inclinação delas é determinada pela expressão.  .
.
Então, particularmente  e
e  , tem inclinações
, tem inclinações
 e
e 
Dado que ambas retas têm a mesma inclinação, podemos concluir que são paralelas. Denominamos essa relação como tal. 
Dado que  , deve-se verificar se são a mesma reta ou diferentes. Para isso, é suficiente encontrar um ponto em comum.
, deve-se verificar se são a mesma reta ou diferentes. Para isso, é suficiente encontrar um ponto em comum.  que não pertença a
que não pertença a  . Com essa ideia em mente, vamos realizar a próxima etapa
. Com essa ideia em mente, vamos realizar a próxima etapa  a equação de
a equação de  para obter
para obter  ; isso implica que
; isso implica que  é um punto na reta
é um punto na reta  mas não é um ponto em
mas não é um ponto em  pois
pois
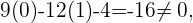
isso confirma que este ponto não satisfaz a equação que define o  . Desta forma, podemos concluir que
. Desta forma, podemos concluir que  e
e  são retas distintas.
são retas distintas.
Agora, vamos encontrar um ponto  de qualquer uma delas e calculamos a distância deste ponto à reta restante. Vamos utilizar
de qualquer uma delas e calculamos a distância deste ponto à reta restante. Vamos utilizar  pois já sabemos que
pois já sabemos que  .
.
Finalmente, usando a fórmula

vamos obter

Uma reta é paralela àquela que tem a seguinte equação  , e é distante
, e é distante  unidades da origem. Qual é sua equação?
unidades da origem. Qual é sua equação?
Vamos chamar a reta que estamos procurando de  . Como sabemos, duas retas são paralelas se os coeficientes
. Como sabemos, duas retas são paralelas se os coeficientes  e
e  respectivos são proporcionais, e como deve ocorrer que
respectivos são proporcionais, e como deve ocorrer que  e, em particular, os coeficientes iguais são proporcionais, a equação que descreve
e, em particular, os coeficientes iguais são proporcionais, a equação que descreve  deve ser da forma
deve ser da forma  .
.
Por outro lado, vamos lembrar que a distância de um ponto  a uma reta
a uma reta  pode ser encontrado através da fórmula
pode ser encontrado através da fórmula

Se o ponto  resulta ser a origem, então a fórmula anterior se reduz a
resulta ser a origem, então a fórmula anterior se reduz a

Isso significa que  deve cumprir com
deve cumprir com

Vamos observar que realmente existe um par de retas que têm distância  com a origem e que são paralelas entre si, é por isso que
com a origem e que são paralelas entre si, é por isso que

>E assim, as equações desse par de retas são dadas por  .
.
Considerando o quadrilátero  cujos vértices são
cujos vértices são  e
e 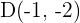 . Calcule a sua área.
. Calcule a sua área.
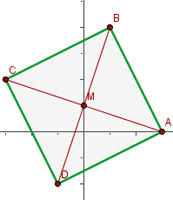
Vamos começar observando que a área que estamos procurando é o resultado da multiplicação das magnitudes  e
e  . Então, vamos proceder com o cálculo de cada magnitude.
. Então, vamos proceder com o cálculo de cada magnitude.


Ao multiplicar os resultados anteriores se obtém


Portanto, a área do quadrilátero é de 20.
Ângulos entre retas
Calcule o ângulo que formam as retas  e
e  , sabendo que seus vetores diretores são:
, sabendo que seus vetores diretores são:  e
e 
Se  e
e  são um par de vetores não nulos, o ângulo formado entre eles é o único número real.
são um par de vetores não nulos, o ângulo formado entre eles é o único número real.  que satisfaz
que satisfaz

onde

e

Fazendo os cálculos correspondentes, temos que



Portanto,
 e assim
e assim 
Calcule o ângulo que formam as retas  e
e 
Para calcular o ângulo que formam duas retas podemos usar a seguinte fórmula:

onde  e
e  as inclinações das retas são
as inclinações das retas são  e
e  respectivamente.
respectivamente.
Uma vez que a equação da reta esteja escrita da forma  , o coeficiente que acompanha
, o coeficiente que acompanha  , isso significa que
, isso significa que  , é a inclinação. Com isso em mente e representado
, é a inclinação. Com isso em mente e representado  e
e  como a seguir
como a seguir
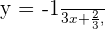

inferimos que  e
e 
Assim, na substituição, obtemos


Portanto  .
.
Encontre uma reta paralela e outra perpendicular a  , que passem pelo ponto
, que passem pelo ponto  .
.
Devemos lembrar que duas retas serão paralelas se tiverem a mesma inclinação. Portanto, para encontrar uma reta paralela a  primeiro devemos conhecer sua inclinação.
primeiro devemos conhecer sua inclinação.
Notamos que a definição de  é equivalente a
é equivalente a

e com esta expressão, podemos facilmente conhecer a inclinação dessa reta, pois é o coeficiente que acompanha a  , ou seja
, ou seja  .
.
Chamando  de reta paralela a
de reta paralela a  que passa pelo ponto
que passa pelo ponto  e
e  em sua inclinação, encontramos que
em sua inclinação, encontramos que  onde
onde  é a inclinação de de
é a inclinação de de  .
.
Agora com as coordenadas de  podemos fazer uso da equação ponto-inclinação da reta, que está descrita por
podemos fazer uso da equação ponto-inclinação da reta, que está descrita por  .
.
Substituindo, entende-se que


Com estes cálculos podemos concluir que  , com
, com  .
.
Para encontrar uma reta perpendicular a  seguiremos o mesmo pensamento anterior, mas com uma condição diferente na inclinação; vamos nomear
seguiremos o mesmo pensamento anterior, mas com uma condição diferente na inclinação; vamos nomear  a reta perpendicular que desejamos encontrar. Neste caso sua inclinação
a reta perpendicular que desejamos encontrar. Neste caso sua inclinação  deve satisfazer a condição
deve satisfazer a condição  para garantir sua perpendicularidade. Então
para garantir sua perpendicularidade. Então  , pois
, pois  .
.
Usando mais uma vez a equação ponto-inclinação da reta e das coordenadas de  , vamos ter que
, vamos ter que

E assim  fica definida pela equação
fica definida pela equação  , onde
, onde  .
.
Encontre a equação da mediatriz do segmento de extremos  e
e  .
.
Dado um segmento, sua mediatriz é o lugar geométrico dos pontos do plano equidistante dos extremos. Em termos matemáticos isso vai se traduzir aos pontos  que satisfazem a igualdade
que satisfazem a igualdade
para  e
e  extremos. Vamos levar em consideração que
extremos. Vamos levar em consideração que
 e
e 
Para encontrar a equação desejada, procedemos igualando essas equações e simplificando os termos.

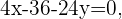
e multiplicando a equação por  podemos simplificar a equação ainda mais, ao obter a expressão
podemos simplificar a equação ainda mais, ao obter a expressão

Encontre as equações das bissetrizes dos ângulos que determinam as retas  e
e  .
.
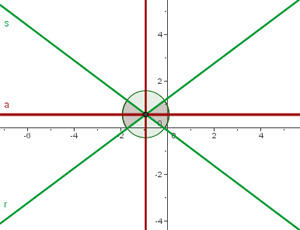
Considerando duas retas que se cruzam, a bissectriz do ângulo que formam é o lugar geométrico dos pontos no plano que ficam equidistantes a estas. Então, vamos procurar a equação que descreva aos pontos  de forma que
de forma que

Por outro lado, a fórmula da distância de um ponto  a uma reta
a uma reta  é dada pela expressão
é dada pela expressão
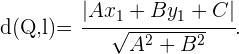
Da fórmula anterior, vamos continuar com

e

Fazendo  , vamos obter
, vamos obter

E multiplicando esta última por  entender que
entender que

Daqui, pelo valor absoluto, vamos obter duas equações:

e

onde cada uma vai descrever a equação, isso nos dará a equação das respectivas bissetrizes.
Para a primeira equação vamos obter

Enquanto que, para a segunda,

Calcule a equação da reta perpendicular a  que passa pelo ponto
que passa pelo ponto  .
.
Vamos notar que a inclinação da reta  é
é  , pois, ao ser expressa na forma
, pois, ao ser expressa na forma  ,a inclinação é simplesmente o coeficiente que acompanha
,a inclinação é simplesmente o coeficiente que acompanha  .
.
Se  é a equação da reta perpendicular a
é a equação da reta perpendicular a  que passa por
que passa por  Então, sua inclinação deve ser
Então, sua inclinação deve ser  , pois o produto de ambas as inclinações deve dar como resultado -1, para obter a ortogonalidade.
, pois o produto de ambas as inclinações deve dar como resultado -1, para obter a ortogonalidade.
Agora com as coordenadas de  podemos fazer uso da equação ponto-inclinação da reta, que está descrita como
podemos fazer uso da equação ponto-inclinação da reta, que está descrita como 
Substituindo, conclui-se que a equação procurada é

ou ao equivale a

Calcule as bissetrizes dos ângulos determinados pelas retas:
Dadas duas retas que se cruzam, a bissetriz do ângulo que forma é o conjunto de pontos no plano que estão equidistantes delas. Portanto, estamos buscando a equação que descreve os pontos  de forma que
de forma que  .
.
Desta forma,

e

Fazendo  , obtemos
, obtemos

E multiplicando esta última por  podemos concluir que
podemos concluir que

A partir disso, ao usar o valor absoluto, obtemos duas equações:
 e
e 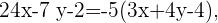
onde cada uma descreverá a equação das respectivas bissetrizes
Para a primeira equação, vamos ter

Enquanto que, para a segunda,

Encontre o ângulo que formam as retas que têm as equações:
a.

b.


a.
Como as equações das retas se encontram em sua forma paramétrica, podemos identificar seus vetores diretores como os coeficientes que acompanham seus parâmetros  . Isso significa que
. Isso significa que  é vetor diretor de
é vetor diretor de  , e
, e  é vetor diretor de
é vetor diretor de  .
.
Aqui, recorrendo à fórmula do ângulo entre vetores:

podemos calcular o ângulo que estamos buscando.
Substituindo as coordenadas de 



b.
Vamos perceber que os vetores diretores dessas retas são  e
e  respectivamente.
respectivamente.
O ângulo formado entre eles é determinado pela expressão



Encontre o ângulo formado pelas retas cujas equações são:
a.

b.

a.
Como primeiro passo, devemos encontrar os vetores diretores de cada uma das retas e, em seguida, calcular o ângulo entre eles. Isso nos dará o ângulo entre  e
e  .
.
Uma reta descrita em sua equação cartesiana  , tem como vetor diretor
, tem como vetor diretor  . Então para
. Então para  e
e  temos vetores diretores
temos vetores diretores  e
e 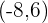 .
.
O ângulo determinado entre esses dois vetores é dado pela fórmula:

Substituindo os vetores diretores que encontramos, vamos ter




b.
Neste caso, os vetores diretores das retas  e
e  são
são  e
e  .
.
Vamos observar que

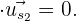
Isso significa que o ângulo entre  e
e  é de 90º, pois a condição
é de 90º, pois a condição 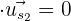 é equivalente a que
é equivalente a que  .
.
Dadas as retas  e
e  , determine
, determine  para que formem um ângulo de
para que formem um ângulo de  .
.
Sejam  e
e  os vetores diretores de
os vetores diretores de  e
e  respectivamente, buscamos
respectivamente, buscamos  de forma que
de forma que
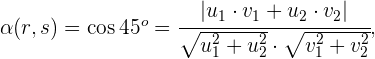
assim, a fórmula anterior nos ajuda a encontrar o ângulo entre duas retas.
Substituindo as coordenadas dos vetores directores e  , vamos obter
, vamos obter
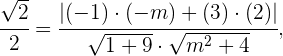
e elevando toda a equação ao quadrado



multiplicando por  toda a equação
toda a equação



Através da fórmula geral para equações ao quadrado

podemos resolver a equação anterior.
Vamos lembrar que  é o coeficiente do termo ao quadrado,
é o coeficiente do termo ao quadrado,  o coeficiente do termo linear e
o coeficiente do termo linear e  o termo independente. Para o nosso caso, eles são determinados da seguinte maneira:
o termo independente. Para o nosso caso, eles são determinados da seguinte maneira:

Portanto, usando a fórmula geral





Em seguida, obtemos que os possíveis valores para satisfazer a condição desejada são  e
e 
Uma reta é perpendicular a que tem como equação  e está distante
e está distante  unidades da origem. Qual é a sua equação?
unidades da origem. Qual é a sua equação?
Para uma reta qualquer  , expressa em sua forma canónica
, expressa em sua forma canónica

tem como coordenadas do seu vetor diretor  .
.
Por outro lado, sabemos que duas retas  são perpendiculares se os seus vetores diretores
são perpendiculares se os seus vetores diretores  são, ou equivalentemente se
são, ou equivalentemente se

onde  . No nosso caso, o vetor diretor de
. No nosso caso, o vetor diretor de  é
é  .
.
Se chamamos de  a reta desejada, seguindo a condição do parágrafo anterior, deve-se obter que o vetor diretor de
a reta desejada, seguindo a condição do parágrafo anterior, deve-se obter que o vetor diretor de  tem como coordenadas
tem como coordenadas  , e assim,
, e assim,  .
.
Por outro lado, vamos recordar que a distância de um ponto  a uma reta
a uma reta  é possível de encontrar através da fórmula
é possível de encontrar através da fórmula
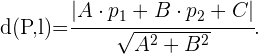
Se o ponto  resulta ser a origem, então a fórmula anterior vai ser reduzida a
resulta ser a origem, então a fórmula anterior vai ser reduzida a
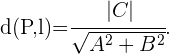
Isso quer dizer que  deve satisfazer a condição
deve satisfazer a condição

Vamos observar que realmente existe um par de retas, que têm uma distância de em relação à origem e são paralelas entre si. É por isso que
em relação à origem e são paralelas entre si. É por isso que

E assim, as equações desse par de retas são dadas por  .
.
Exercícios avançados
Considerando o triângulo  ; calcule as equações das alturas e determinar o ortocentro de um triângulo.
; calcule as equações das alturas e determinar o ortocentro de um triângulo.
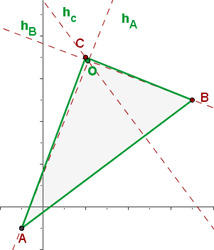
Como primeiro passo, vamos calcular as equações das alturas do triângulo definido. Vamos chamar e
e  às equações das retas que passam pelos pontos
às equações das retas que passam pelos pontos  e
e  respectivamente.
respectivamente.
Para  temos que
temos que  , isso significa que a inclinação
, isso significa que a inclinação  do segmento
do segmento  multiplicada pela inclinação
multiplicada pela inclinação  de
de  deve dar como resultado
deve dar como resultado 
Conhecendo as coordenadas dos pontos  e
e  podemos obter sua inclinação através da fórmula
podemos obter sua inclinação através da fórmula  . Portanto
. Portanto
 e
e
Com as coordenadas de  ,
,  e a forma ponto-inclinação, podemos deduzir a equação da reta é
e a forma ponto-inclinação, podemos deduzir a equação da reta é  . Então
. Então  é a equação que define
é a equação que define  .
.
Simplificando esta última, temos que  .
.
Seguindo o mesmo raciocínio, podemos encontrar as equações restantes
Vamos começar pelas inclinações.
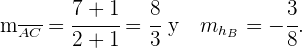
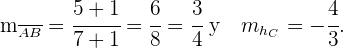
Em seguida, com a fórmula ponto-inclinação para 


e para 


Para encontrar as coordenadas do ortocentro basta encontrar a interseção de qualquer uma das duas alturas.
Resolvendo o sistema de equações lineares

encontramos que o ortocentro se encontra situado em 
Dado o triângulo  ; calcule as equações das medianas e determinar o baricentro do triângulo.
; calcule as equações das medianas e determinar o baricentro do triângulo.
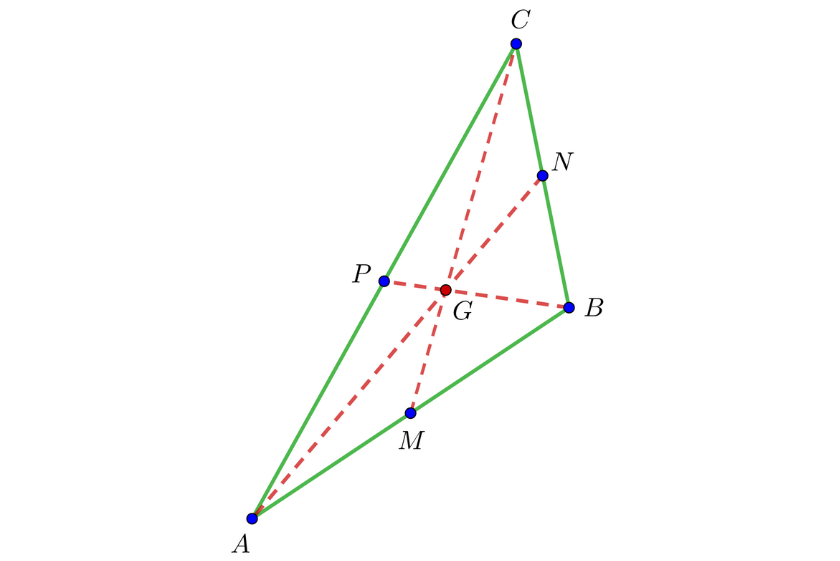
Como primeiro passo, vamos calcular os pontos médios dos lados do triângulo definido. Vamos chamar de  aos pontos médios de
aos pontos médios de  , respectivamente
, respectivamente
 ,
,
 ,
,
 ,
,
Vamos calcular as equações das medianas do triângulo definido. Vamos chamar  e
e  às equações das medianas que passam pelos pontos
às equações das medianas que passam pelos pontos  e
e  respectivamente.
respectivamente.
Ao conhecer as coordenadas dos pontos  e
e  podemos obter sua inclinação através da fórmula
podemos obter sua inclinação através da fórmula  . Portanto
. Portanto



Com as coordenadas de  ,
,  e a fórmula ponto-inclinação, podemos deduzir a equação da reta para
e a fórmula ponto-inclinação, podemos deduzir a equação da reta para  . Então
. Então  é a equação que define
é a equação que define  .
.
Simplificando esta última, obtemos que  .
.
Seguindo o mesmo raciocínio, podemos encontrar as equações que faltam.
 .
.
 .
.
Para encontrar as coordenadas do baricentro, basta encontrar a interseção de quaisquer duas medianas.
Resolvendo o sistema de equações lineares

encontramos que o baricentro está localizado em 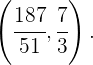
Considerando o triângulo  ; calcular as equações das mediatrizes e determinar o circuncentro do triângulo.
; calcular as equações das mediatrizes e determinar o circuncentro do triângulo.
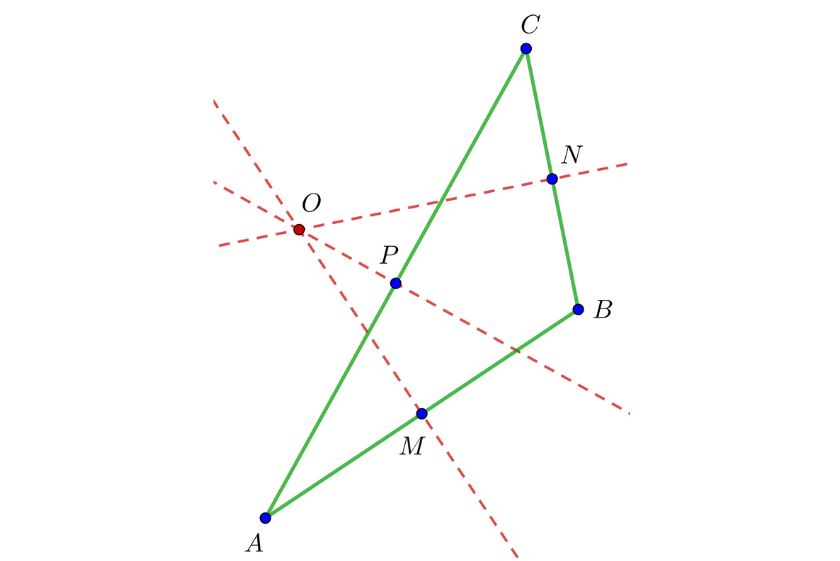
Como primeiro passo, calculemos os pontos médios dos lados do triângulo definido. Vamos chamar de  os pontos médios de
os pontos médios de  , respectivamente
, respectivamente
 ,
,
 ,
,
 ,
,
Vamos calcular as equações das mediatrizes do triângulo definido. Vamos chamar  e
e  às equações das mediatrizes que passam pelos pontos médios
às equações das mediatrizes que passam pelos pontos médios  e
e  respectivamente.
respectivamente.
Ao conhecer as coordenadas dos puntos  e
e  podemos obter a inclinação dos lados através da fórmula
podemos obter a inclinação dos lados através da fórmula  e sabendo que a inclinação da sua perpendicular é o recíproco negativo da inclinação, vamos ter
e sabendo que a inclinação da sua perpendicular é o recíproco negativo da inclinação, vamos ter



Com as coordenadas de  ,
,  e a forma ponto-inclinação, podemos deduzir a equação da reta para
e a forma ponto-inclinação, podemos deduzir a equação da reta para  . Então
. Então  é a equação que define
é a equação que define  .
.
Simplificando esta última, temos que  .
.
Seguindo o mesmo raciocínio, podemos encontrar as equações restantes.
 .
.
 .
.
Para encontrar as coordenadas do circuncentro, é suficiente encontrar a interseção de quaisquer duas mediatrizes
Resolvendo o sistema de equações lineares

encontramos que o circuncentro está localizado em 
Uma reta com a equação  é mediatriz de um segmento
é mediatriz de um segmento  cujo extremo
cujo extremo  tem as coordenadas
tem as coordenadas  . Encontre as coordenadas do outro extremo.
. Encontre as coordenadas do outro extremo.
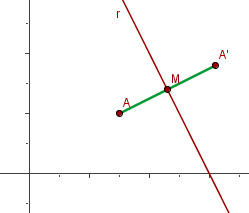
Vamos chamar de  à equação que descreve a reta sobre a qual repousa o segmento
à equação que descreve a reta sobre a qual repousa o segmento  e o ponto
e o ponto  .
.
Note que, ao ser  mediatriz do segmento
mediatriz do segmento  se satisfaz com
se satisfaz com  , o que implica que
, o que implica que  onde
onde  e
e  são as inclinações respectivas das retas
são as inclinações respectivas das retas  e
e  .
.
Do raciocínio anterior obtemos que  , pois expressando
, pois expressando  em sua forma equivalente
em sua forma equivalente  , sabemos que
, sabemos que  .
.
Com a equação ponto-inclinação, podemos encontrar a equação que descreve a reta que passa pelo ponto  e tem inclinação
e tem inclinação  . Basta reduzir a expressão
. Basta reduzir a expressão  e obter
e obter  .
.
Agora, vamos observar que  , o ponto de interseção entre
, o ponto de interseção entre  e
e  , Deve satisfazer ambas as equações, a que descrever
, Deve satisfazer ambas as equações, a que descrever  e
e  . É através deles que vamos encontrar as coordenadas de
. É através deles que vamos encontrar as coordenadas de  , basta resolver o sistema de equações
, basta resolver o sistema de equações

Resolvendo o sistema, obtemos que as coordenadas do ponto  são
são  . Além disso,
. Além disso,  é o ponto médio do segmento
é o ponto médio do segmento  , o que matematicamente significa que
, o que matematicamente significa que

onde  são as coordenadas de
são as coordenadas de  respectivamente.
respectivamente.
Igualando coordenada por coordenada, vamos obter que

Substituindo os valores que já conhecemos de  e
e  concluimos que
concluimos que

e assim

Portanto, o extremo  tem como coordenadas
tem como coordenadas  .
.
Encontre o ponto simétrico  , do ponto
, do ponto  , com relação à reta
, com relação à reta 
Vamos chamar de  a equação que descreve a reta em que descansa o segmento
a equação que descreve a reta em que descansa o segmento  e o ponto
e o ponto  . Dadas nossas hipóteses, deve ser satisfeito que
. Dadas nossas hipóteses, deve ser satisfeito que  , isso implica que
, isso implica que  , onde
, onde  e
e  são as respectivas inclinações das retas.
são as respectivas inclinações das retas.  e
e  .
.
Por outro lado, a equação de  em sua forma explícita é
em sua forma explícita é  , e desta maneira, a inclinação de
, e desta maneira, a inclinação de  é simplemente o coeficiente que acompanha x, ou seja
é simplemente o coeficiente que acompanha x, ou seja  . Com essa última parte, podemos concluir que
. Com essa última parte, podemos concluir que  .
.
Com a equação ponto-inclinação, podemos encontrar a equação que descreve a reta que passa pelo ponto  e tem inclinação
e tem inclinação  . Basta reduzir a expressão a
. Basta reduzir a expressão a

e obter
 .
.
Agora, vamos observar que  , o ponto de interseção entre
, o ponto de interseção entre  e
e  , deve satisfazer ambas equações: a que descreve
, deve satisfazer ambas equações: a que descreve  e
e  . É através deles que para encontrar as coordenadas de
. É através deles que para encontrar as coordenadas de  , basta resolver o sistema de equações
, basta resolver o sistema de equações

Resolvendo o sistema, obtemos as coordenadas do ponto  são
são  . Além do mais,
. Além do mais,  é o ponto médio do segmento
é o ponto médio do segmento  ,e em termos matemáticos, é equivalente a
,e em termos matemáticos, é equivalente a

donde  são as coordenadas de
são as coordenadas de  respectivamente.
respectivamente.
Igualando coordenada por coordenada, se obtém que

E substituindo os valores que já conhecemos de  e
e  se deduz que
se deduz que

e, assim

Portanto, o ponto simétrico  tem como coordenadas
tem como coordenadas  .
.
Resumir com IA:












