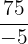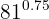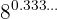Bem-vindo aos exercícios sobre números reais! Os números reais são fundamentais na Matemática e englobam uma ampla variedade de valores, incluindo os números inteiros, fracionários, decimais, racionais e irracionais. Eles se estendem infinitamente para os dois lados da reta numérica e servem de base para a realização de operações matemáticas essenciais.
Ao longo desta série de atividades, você colocará em prática seus conhecimentos sobre diferentes conceitos relacionados aos números reais. Lembre-se de que os números reais são uma ferramenta poderosa para representar quantidades e medidas no nosso dia a dia, além de serem amplamente utilizados em diversas áreas acadêmicas e profissionais.
O estudo desse conjunto numérico é também essencial para a compreensão de conteúdos mais avançados em Matemática e Ciências.
Bora lá! Mergulhe nos exercícios e aproveite para fortalecer suas habilidades com os números reais.
Classifique os números:
a. 
Note que  é um número irracional, ou seja,
é um número irracional, ou seja, 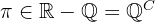 , em que
, em que 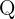 são números racionais. Sabemos que o que o produto, a divisão, a soma ou a subtração entre um número irracional e um número racional tem como resultado um número irracional. Assim, temos que
são números racionais. Sabemos que o que o produto, a divisão, a soma ou a subtração entre um número irracional e um número racional tem como resultado um número irracional. Assim, temos que  é irracional.
é irracional.

b. 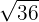
Observe que podemos resolver a raiz de forma exata, ou seja, 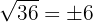 , onde
, onde  e
e  são números inteiros, portanto:
são números inteiros, portanto:
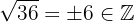
c. 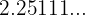
Todo número que apresenta uma dízima periódica pode ser expresso como uma fração. Isso significa que todo número com dízima periódica é um número racional. De fato, temos:
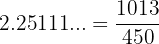
Isso comprova que se trata de um número racional.
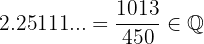
d. 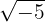
As raízes de números negativos nunca pertenceram ao conjunto dos números reais. Esses números fazem parte de uma extensão dos números reais conhecida como números complexos, representados por 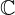 . Dito isso, esse número é um número complexo.
. Dito isso, esse número é um número complexo.
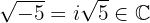
e. 
Ao termos uma fração formada por números inteiros, é claro que estamos lidando com um número racional. No entanto, ao realizar a divisão, percebemos que essa fração é equivalente a um número inteiro. 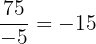 . Sendo assim:
. Sendo assim:
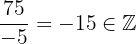
Represente na reta numérica: 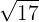
Para localizá-lo, primeiro observamos que ao calcular a raiz quadrada, temos:
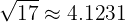
Vamos marcar esse ponto na reta numérica:
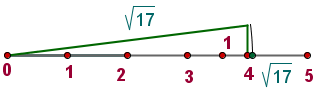
Represente na reta real os números que satisfazem as seguintes relações:
a. 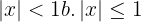
c. 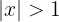
d. 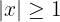
Represente na reta real os números que satisfazem as seguintes relações:
a. \left | x \right | < 1
Pela definição de valor absoluto, as seguintes igualdades são equivalentes:
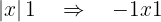
Onde a última desigualdade implica:  .
.

b. 
Conforme a definição do valor absoluto, as seguintes igualdades são equivalentes:

Em que a última desigualdade implica que  .
.

c. 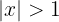
Pela definição de valor absoluto, as seguintes igualdades são equivalentes:
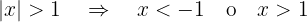 .
.
Onde a última desigualdade implica que  ou
ou 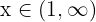 , o que podemos expressar em termos de união de conjuntos da seguinte forma:
, o que podemos expressar em termos de união de conjuntos da seguinte forma: 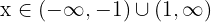 .
.
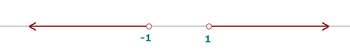
d. 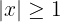
Sabemos que, de acordo com a definição do valor absoluto, as seguintes igualdades são equivalentes:
 .
.
E a última desigualdade implica que  o
o  , o que podemos expressar em termos de união de conjuntos da seguinte forma:
, o que podemos expressar em termos de união de conjuntos da seguinte forma:  .
.

Calcule os valores das potências a seguir:
a. 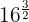
Uma potência com expoente fracionário é equivalente a uma raiz cujo índice é o denominador da fração  e o numerador da fração é o expoente do radicando
e o numerador da fração é o expoente do radicando 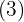 .
.
Vamos decompor o 16 em fatores, fazer as contas dentro da raiz e depois simplificar o resultado:
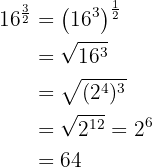
b. 
Uma potência com expoente fracionário é equivalente a uma raiz cujo índice é o denominador da fração 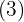 e o numerador da fração é o expoente do radicando
e o numerador da fração é o expoente do radicando  .
.
Vamos decompor o 8 em fatores, fazer as contas dentro da raiz e depois simplificar o resultado:
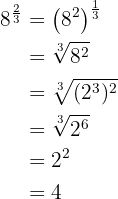
c. 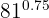
Neste caso, transformamos o expoente, que é um número decimal exato, em uma fração.
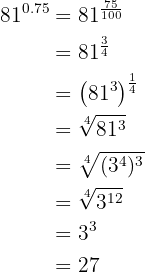
d. 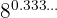
Como se trata de um expoente com dízima periódica simples, podemos representá-lo como uma fração: 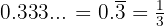 . Sendo assim:
. Sendo assim:
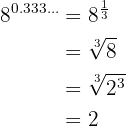
Encontre o valor das seguintes somas:
Vamos resolver os exercícios decompondo o radicando em fatores primos. Em seguida, usando operações básicas (soma e subtração), encontraremos as soluções.
a. 
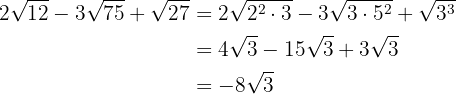
b. 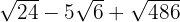
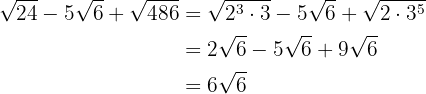
c. 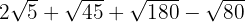
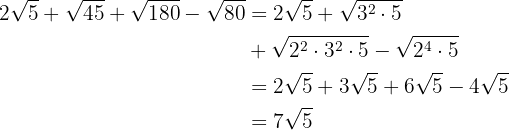
d. 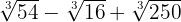
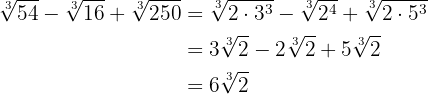
Faça as operações:
Para resolver este exercício, vamos aplicar a teoria que já conhecemos sobre potências e multiplicação de binomios.
a. 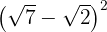
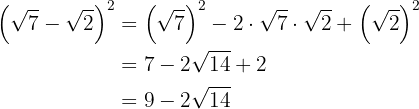
b. 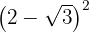
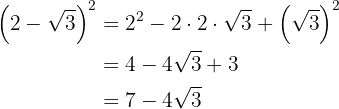
c. 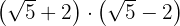
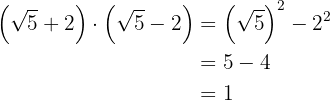
d. 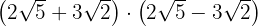
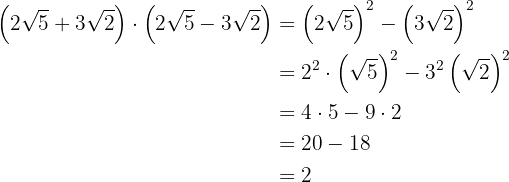
Resolva essa operação:
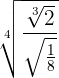
Para resolver este exercício, vamos aplicar a teoria de expoentes que já conhecemos. Trabalharemos com as frações nos expoentes da expressão dada, simplificando-a passo a passo até chegar à forma mais reduzida possível:
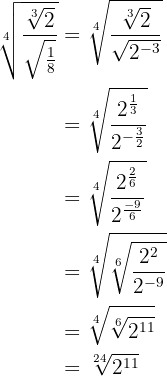
Faça essa operação: 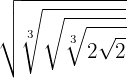
Para resolver este exercício, usaremos a equivalência entre potências fracionárias e radicais. Isso nos permitirá simplificar a expressão passo a passo:
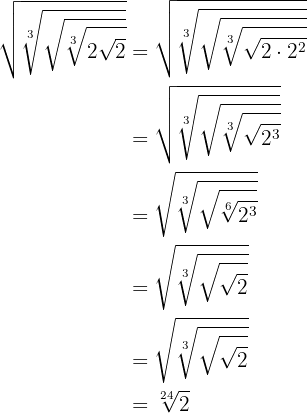
Calcule:
Aplicaremos o que sabemos de álgebra para efetuar esses cálculos:
a. 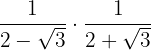
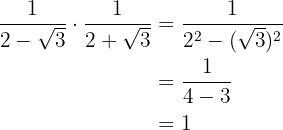
b. 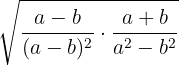
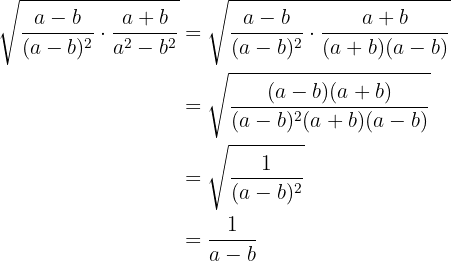
Elimine os radicais do denominador:
Lembre-se que, para eliminar os radicais do denominador de uma fração, é preciso multiplicá-la por um '1 multiplicativo' adequado.
a. 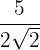
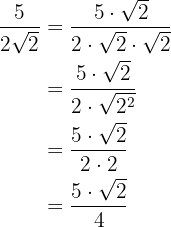
b. 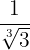
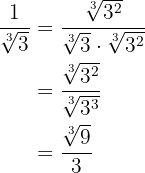
c. 
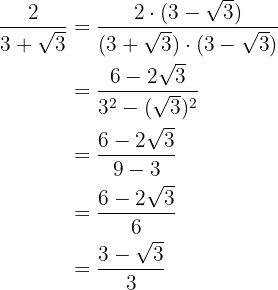
d. 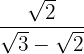
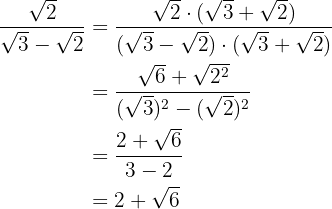
Resumir com IA: