Seja bem-vindo à nossa página dedicada a problemas e exercícios resolvidos sobre equações do segundo grau! Neste espaço, vamos explorar o universo dessas equações e oferecer ferramentas práticas para que você compreenda e resolva esse conteúdo essencial da matemática.
As equações do segundo grau (também conhecidas como equações quadráticas) fazem parte da base do estudo matemático e têm aplicações diversas em áreas como a física, a economia e a engenharia. Essas equações se caracterizam por apresentarem uma incógnita elevada ao quadrado e podem possuir uma ou duas soluções reais.
Aqui, você encontrará uma variedade de problemas: desde exercícios de fatoração, passando pela completação do quadrado, até a aplicação da fórmula de Bhaskara. Cada resolução será acompanhada de explicações claras, passo a passo, para que você compreenda não só o que fazer, mas por que fazer.
Além disso, vamos aplicar esses conhecimentos em situações do dia a dia, para mostrar como a matemática está presente em muitos contextos da vida real.
Nosso objetivo é ajudar você a entender melhor as equações do segundo grau, aprimorar suas habilidades de resolução de problemas e ganhar mais confiança em matemática. Prepare-se para mergulhar nesse conteúdo e descobrir como essas equações podem ser úteis e até divertidas!
Resolva as equações:
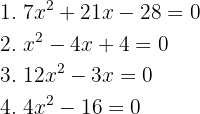
1 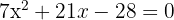
Pode ser resolvida utilizando a fórmula de Bhaskara ou o método da fatoração. Aplicando o método da fatoração:
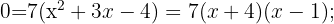

2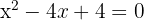
Aplicando o método da fatoração:
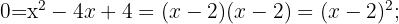
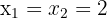
3
Aplicando o método da fatoração:


4
Aplicando o método da fatoração:


Resolva as equações:
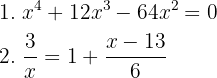
1 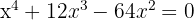
Aplicando o método da fatoração:

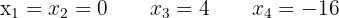
2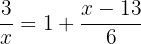
Escrevemos o segundo membro com denominador comum e realizamos o produto cruzado entre os membros da equação pelos denominadores. Em seguida, aplicamos o método da fatoração:
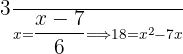


Resolva as equações:
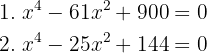
1
Aplicando o método da fatoração:
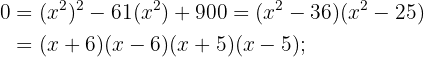

2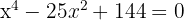
Aplicando o método da fatoração:
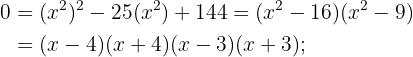

Resolva as equações:
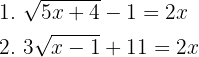
1
Primeiro, isolamos a raiz da equação. Em seguida, elevamos ambos os lados ao quadrado, desenvolvemos as potências e resolvemos a equação:

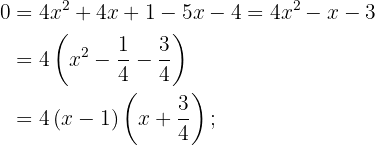

2 
Isolamos a raiz. Depois, elevamos ambos os membros ao quadrado, desenvolvemos os termos e resolvemos usando a fórmula de Bhaskara:

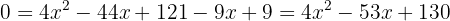
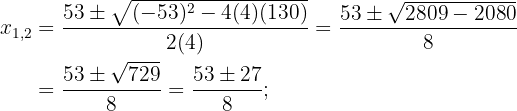
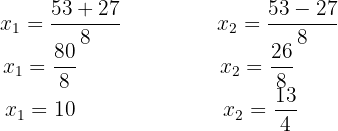
Encontre as raízes:
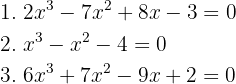
1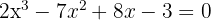
Utilizamos a divisão sintética, já que se trata de uma equação do terceiro grau. Os divisores de  são
são 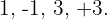 Dessa forma:
Dessa forma:
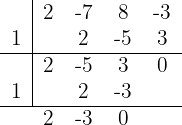
Logo, a fatoração é: 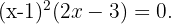
Portanto: 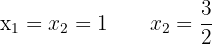
2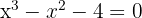
Usamos a divisão sintética, já que se trata de uma equação de terceiro grau. Os divisores de  são
são 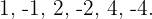 Assim,
Assim,
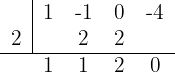
Então, a fatoração é 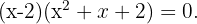 Ao calcular o discriminante do trinômio, conclui-se que ele não possui raízes reais, pois o resultado é negativo.
Ao calcular o discriminante do trinômio, conclui-se que ele não possui raízes reais, pois o resultado é negativo.
Portanto, há apenas uma solução real:
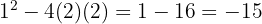
Utiliza-se a divisão sintética, pois a equação é do terceiro grau. Os divisores de  são:
são:  Así:
Así:
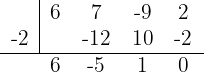
Então, a fatoração é (x+2)(6x2−5x+1)=0(x + 2)(6x^2 - 5x + 1) = 0 
Resolve-se a equação quadrática pela fórmula de Bhaskara:
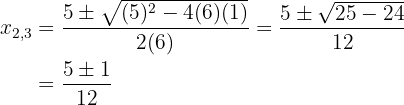
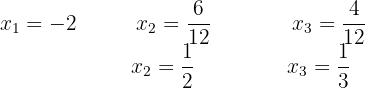
Resolva as equacões
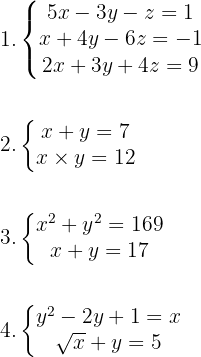
1
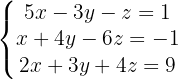
Vamos construir a matriz aumentada do sistema e aplicar operações elementares entre as linhas:
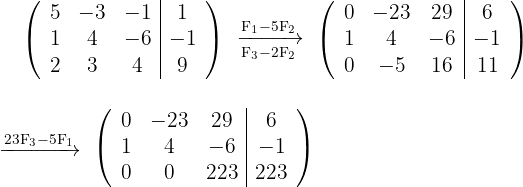
Então, 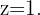 Substituindo na matriz, obtemos:
Substituindo na matriz, obtemos:  uma vez que:
uma vez que:
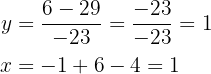
2
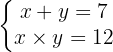
Isolamos uma incógnita na primeira equação e substituímos na segunda. Depois, resolvemos a equação do segundo grau:
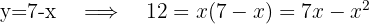
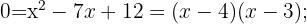

3
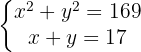
Isola-se uma das incógnitas na segunda equação e substitui-se a expressão obtida na primeira. Em seguida, resolve-se a equação do segundo grau.
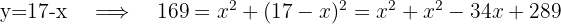


4
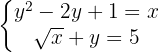
Substitui-se a expressão que representa  na segunda equação. Em seguida, eleva-se ao quadrado ambos os membros da equação e resolve-se.
na segunda equação. Em seguida, eleva-se ao quadrado ambos os membros da equação e resolve-se.
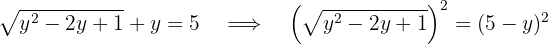


Determine o valor de  para que as soluções da equação
para que as soluções da equação  sejam do mesmo valor.
sejam do mesmo valor.
Calcula-se o discriminante e iguala-se a zero. Assim, obtém-se uma raiz dupla.
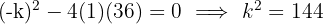
Os valores possíveis do coeficiente do termo linear são: 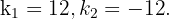
Encontre o valor de dois números cuja a soma seja cinco e cujo produto seja 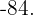

Os números são:  e
e  .
.
Determinar a idade de Pedro, sabendo que daqui a  anos ele terá a metade do quadrado da idade que tinha há
anos ele terá a metade do quadrado da idade que tinha há  anos.
anos.
Se considerarmos  como a idade atual de Pedro, então há
como a idade atual de Pedro, então há  anos ele tinha
anos ele tinha 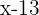 e daqui a
e daqui a  anos terá
anos terá  :
: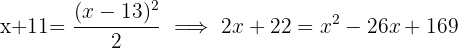

Portanto, Pedro tem  anos.
anos.
Para cercar uma fazenda retangular de  foram utilizados
foram utilizados 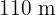 de tela alambrado para cerca
de tela alambrado para cerca
Calcule as dimensões da fazenda.
Dividindo pela metade a quantidade de tela alambrado utilizada, obtemos o semiperímetro da fazenda, 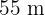 .
.
Portanto, o problema pode ser modelado com as expressões da imagem:


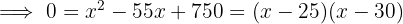
A fazenda tem as seguintes dimensões: 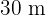 e
e 
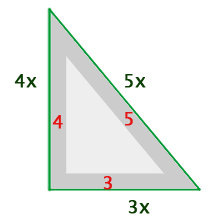
Os três lados de um triângulo retângulo são proporcionais aos números  Calcule o comprimento de cada lado do triângulo sabendo que sua área é
Calcule o comprimento de cada lado do triângulo sabendo que sua área é 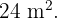
As medidas dos lados do triângulo são obtidas multiplicando-se por um fator  os lados do triângulo retângulo da imagem. A partir da fórmula da área, pode-se encontrar esse fator:
os lados do triângulo retângulo da imagem. A partir da fórmula da área, pode-se encontrar esse fator:
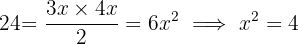
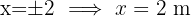
Os lados do triângulo são: 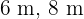 e
e 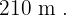
Um jardim retangular de 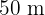 de largura por
de largura por  de largura está rodeado por um caminho de areia com largura uniforme.
de largura está rodeado por um caminho de areia com largura uniforme.
Calcule a largura desse caminho, sabendo que ele possui uma área de 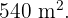
Ao considerar uma largura  do caminho de areia, temos um retângulo maior com dimensões
do caminho de areia, temos um retângulo maior com dimensões 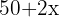 por
por  , conforme indicado na figura. Agora, expressamos a área do caminho de areia:
, conforme indicado na figura. Agora, expressamos a área do caminho de areia:


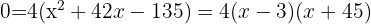
Portanto, a largura do caminho é de 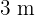 de largo.
de largo.
Calcule as dimensões de um retângulo cuja diagonal mede 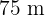 , sabendo que ele é semelhante a outro retângulo de
, sabendo que ele é semelhante a outro retângulo de 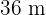 por
por 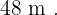
Como o retângulo de 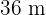 por
por 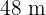 é semelhante ao retângulo de
é semelhante ao retângulo de 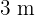 por
por  o retângulo cuja diagonal é
o retângulo cuja diagonal é 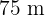 . Podemos assumir,também terá lados proporcionais, com um fator
. Podemos assumir,também terá lados proporcionais, com um fator  , conforme a imagem.
, conforme a imagem.
Se aplica el teorema de Pitágoras y se halla el valor de la incógnita. Aplicamos o teorema de Pitágoras para encontrar o valor da incógnita:
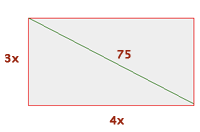
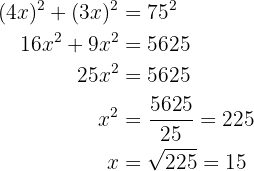
Portanto, o retângulo tem 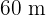 de largura.
de largura.
Calcule dois números naturais cuja diferença seja dois e cuja soma dos quadrados seja 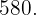
Considerando que a diferença entre os dois números é dois, se  representa um deles, o outro será
representa um deles, o outro será 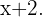
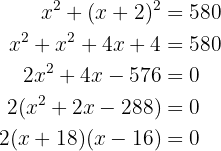
Os números são  e
e 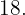
Duas mangueiras A e B enchem juntas uma piscina em duas horas. A mangueira A enche a piscina em três horas a menos que a mangueira B. Calcule quantas horas cada uma demora, individualmente, para encher a piscina.
Se a mangueira A demora  horas para encher a piscina, então a mangueira B demorará
horas para encher a piscina, então a mangueira B demorará  horas para encher a piscina.
horas para encher a piscina.
Assim, a cada hora, a mangueira A enche  partes da piscina e a mangueira B enche
partes da piscina e a mangueira B enche 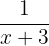 partes da piscina. Como as duas mangueiras juntas enchem a piscina por completo, temos:
partes da piscina. Como as duas mangueiras juntas enchem a piscina por completo, temos:
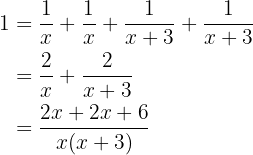
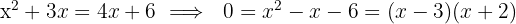
Assim, a mangueira A leva  horas para encher a piscina sozinha e a mangueira B leva
horas para encher a piscina sozinha e a mangueira B leva  horas.
horas.
Determine dois números tais que o produto entre eles seja quatro e a soma de seus quadrados seja dezessete.
Vamos formular o sistema com duas incógnitas e resolver:
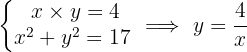

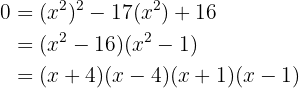
Os dois pares números possíveis são: 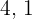 e
e 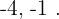
Encontre uma fração equivalente a  cujos termos elevados ao quadrado somem:
cujos termos elevados ao quadrado somem: 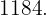
Vamos formular o sistema com duas incógnitas e resolver:
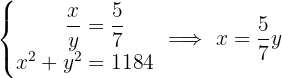
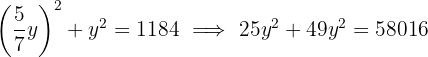
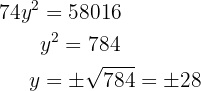
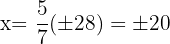
A fração que satisfaz a condição é:
 , pois em
, pois em 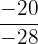 são cancelados os sinais negativos e obtemos a primeira fração.
são cancelados os sinais negativos e obtemos a primeira fração.
Um cliente pagou um total de R$ 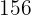 por
por  l de leite,
l de leite,  kg de presunto serrano e
kg de presunto serrano e  l de azeite de oliva.
l de azeite de oliva.
Calcule o preço cada ítem, sabendo que 1 litro de azeite custa o triplo que 1 litro de leite e que 1 kg presunto serrano custa o mesmo que comprar  litros de azeite mais
litros de azeite mais  l de leite.
l de leite.
Sejam  os preços do leite, do presunto serrano e do azeite de oliva, respectivamente.
os preços do leite, do presunto serrano e do azeite de oliva, respectivamente.
Forma-se o sistema de equações correspondente e resolve-se:
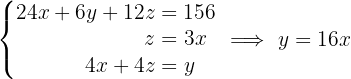
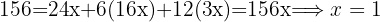

Portanto, o leite custa R$ 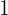 litro, o presunto serrano R$
litro, o presunto serrano R$ 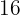 o quilo e o azeite de oliva, R$
o quilo e o azeite de oliva, R$ 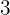 o litro.
o litro.
Uma locadora de filmes é especializado em filmes de três tipos: infantis, faroeste americano e terror. Sabe-se que:
 dos filmes infantis mais
dos filmes infantis mais 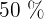 dos de faroeste representam
dos de faroeste representam  do total de filmes.
do total de filmes.
Determine o número de filmes de cada tipo, sabendo que há  filmes a mais de faroeste do que infantis.
filmes a mais de faroeste do que infantis.
Sejam  os filmes infantis, de faroeste e de terror, respectivamente.
os filmes infantis, de faroeste e de terror, respectivamente.
Forma-se o sistema de equações correspondente e resolve-se:
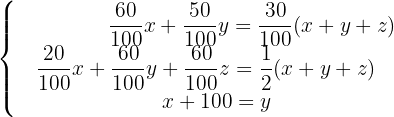
Simplificando o sistema de equações, vamos ter:
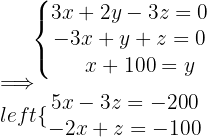
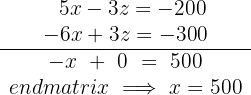
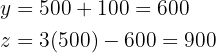
A locadora de vídeos tem  filmes infantis,
filmes infantis,  faroeste e
faroeste e 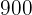 de terror.
de terror.
Resumir com IA:


