Bem-vindos à nossa seção dedicada à resolução de equações lineares e sua aplicação em uma ampla variedade de problemas. As equações lineares são a base das matemáticas e têm uma ampla gama de aplicações em diversos campos, desde a física até a economia. Neste guia, acompanharemos vocês em uma jornada de aprendizado que abrange tanto a resolução de equações lineares quanto sua aplicação em situações do mundo real.
A resolução de uma equação linear envolve encontrar o valor ou os valores de uma variável desconhecida que tornam a equação verdadeira. É um processo sistemático que exige manipulação algébrica cuidadosa. Além disso, aprenderemos a aplicar equações lineares para resolver problemas práticos em diversas disciplinas.
É fundamental lembrar que o conhecimento e a aplicação das equações lineares são habilidades essenciais em matemática e na resolução de problemas cotidianos. Ao longo deste guia, exploraremos exercícios que nos ajudarão a entender como usar essa ferramenta matemática para analisar e resolver situações que podemos encontrar no nosso dia a dia.

Exercícios de equações
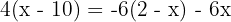
Realizamos as multiplicações em ambos os lados da equação: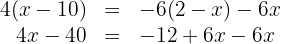
Somamos e subtraímos os termos semelhantes nos lados da equação: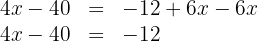
Para isolar  , primeiro somamos
, primeiro somamos  em ambos os lados da equação e simplificamos:
em ambos os lados da equação e simplificamos: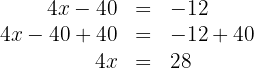
Para obter  , agora multiplicamos por
, agora multiplicamos por  em ambos os lados da equação e novamente, simplificamos:
em ambos os lados da equação e novamente, simplificamos: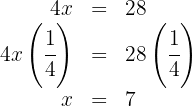
Assim,  é a solução da equação.
é a solução da equação.

Realizamos as multiplicações: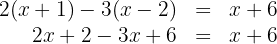
Somamos e subtraímos os termos semelhantes nos dois lados da equação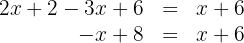
Para isolar  , primeiro subtraímos
, primeiro subtraímos  e
e  em ambos os lados da equação e simplificamos
em ambos os lados da equação e simplificamos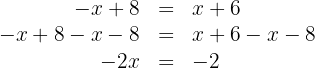
Para obter  , agora multiplicamos por
, agora multiplicamos por  em ambos os lados da equação e mais uma vez, simplificamos:
em ambos os lados da equação e mais uma vez, simplificamos: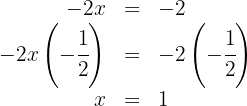
Assim,  é a solução da equação.
é a solução da equação.
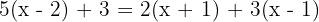
Realizamos as multiplicações: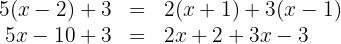
Somamos e subtraímos os termos semelhantes dos dois lados da equação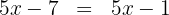
Subtraímos  de ambos os lados
de ambos os lados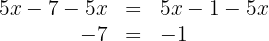
Como não é possível, portanto, a equação não tem solução.
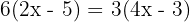
Realizamos as multiplicações: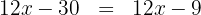
Subtraímos  de ambos os lados
de ambos os lados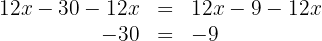
Isso não é possível, então, a equação não tem solução.
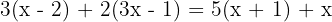
Realizamos as multiplicações: 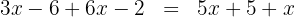
Somamos e subtraímos os termos semelhantes: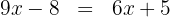
Para isolar  , subtraímos
, subtraímos  e somamos
e somamos  em ambos os lados:
em ambos os lados: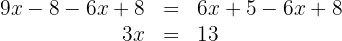
Dividimos os dois lados por 
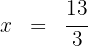
Assim, 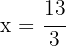 é a solução da equação.
é a solução da equação.
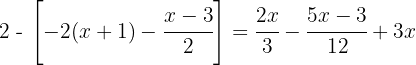
Vamos remover os colchetes: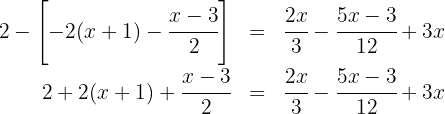
Calculamos o 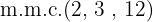 dos denominadores:
dos denominadores: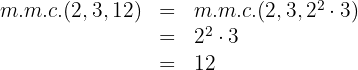
Multiplicamos os dois lados da equação pelo 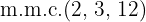 :
: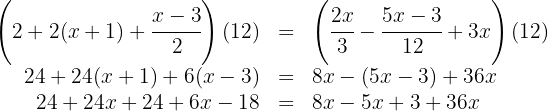
Somamos e subtraímos os termos semelhantes: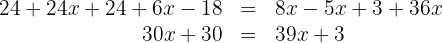
Subtraímos 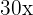 e
e  em ambos os lados da equação:
em ambos os lados da equação: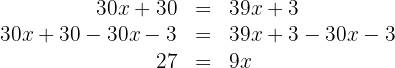
Multiplicamos ambos os lados da equação por 
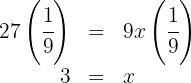
Assim,  é a solução da equação.
é a solução da equação.
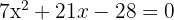
Resolvemos utilizando a fórmula de Bhaskara para encontrar as raízes da equação do segundo grau: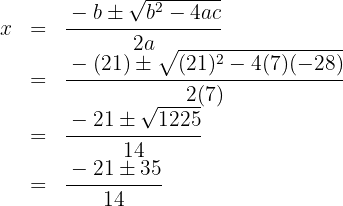
As raízes são:
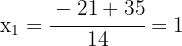
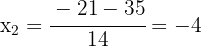
As raízes da equação são suas soluções. Assim, as soluções são  e
e 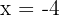 .
.

Resolvemos utilizando a fórmula de Bhaskara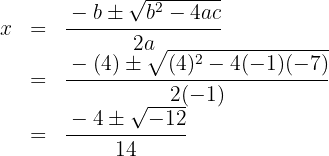
Como não existem raízes reais para números negativos, concluímos que a equação não tem soluções reais.

Resolvemos utilizando a fórmula de Bhaskara: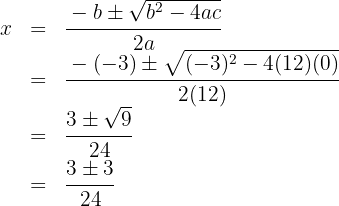
As raízes são:
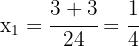
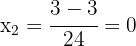
As raízes da equação são suas soluções. Assim, as soluções são:  e
e  .
.
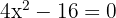
Resolvemos utilizando a fórmula de Bhaskara: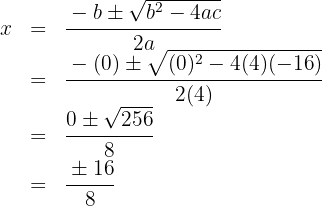
As raízes são:
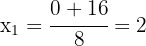
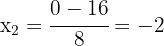
As raízes da equação são suas soluções. Assim, as soluções são:  e
e  .
.
Problemas de aplicação
Um pai tem 35 anos e seu filho tem 5. Em quantos anos a idade do pai será três vezes maior que a idade do filho?
A idade atual do pai é 35 anos e a do filho é 5 anos, enquanto  são os anos que precisam passar para que satisfaça a condição do problema.
são os anos que precisam passar para que satisfaça a condição do problema.
Escrevemos a condição dada na forma de uma equação:
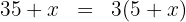
Realizamos a multiplicação: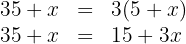
Subtraímos  e
e  de ambos os lados da equação
de ambos os lados da equação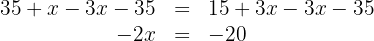
Para isolar  , multiplicamos ambos os lados da equação por
, multiplicamos ambos os lados da equação por  e simplificamos:
e simplificamos: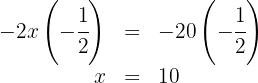
Portanto, daqui a  anos, a idade do pai será três vezes maior que a do filho.
anos, a idade do pai será três vezes maior que a do filho.
Se o dobro de um número for subtraída sua metade, o resultado é 54. Qual é o número?
Como não conhecemos o número solicitado, representamos por  .
.
Escrevemos a condição fornecida na forma de uma equação
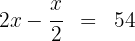
Multiplicamos ambos os lados da equação por dois: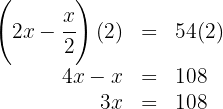
Multiplicamos os dois lados da equação por 
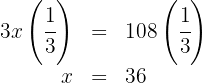
O número procurado é 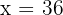 .
.
A base de um retângulo é o dobro de sua altura. Quais são suas dimensões se o perímetro mede 30 cm?
Representamos a altura por  , logo, sua base é
, logo, sua base é  .
.
Em uma reunião, há o dobro de mulheres do que homens e o triplo de crianças do que de homens e mulheres juntas. Quantos homens, mulheres e crianças há, se a reunião é composta por 96 pessoas?
Representamos o número de homens por  , então o número de mulheres é
, então o número de mulheres é  e o número de crianças é
e o número de crianças é 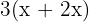 .
.
Escrevemos a condição dada na forma de uma equação:
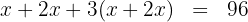
Realizamos as multiplicações e somamos os termos semelhantes: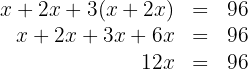
Multiplicamos ambos os lados da equação por: 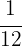
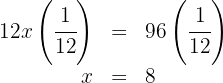
Sendo assim, o número de homens é  , o de mulheres é
, o de mulheres é 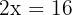 e o de crianças é
e o de crianças é 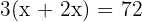 .
.
Foram consumidos  de um galão de óleo. Repondo
de um galão de óleo. Repondo 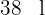 , o galão ficou cheio até
, o galão ficou cheio até  da sua capacidade. Calcule a capacidade total do galão.
da sua capacidade. Calcule a capacidade total do galão.
Vamos chamar de  a capacidade do galão e, como foi consumido
a capacidade do galão e, como foi consumido  de sua capacidade, sobrou
de sua capacidade, sobrou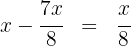
Ao repor 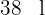 , escrevemos a segunda condição dada na forma de uma equação
, escrevemos a segunda condição dada na forma de uma equação
Multiplicamos ambos os lados da equação pelo 
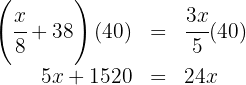
Subtraímos 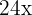 e
e  de ambos os lados da equação
de ambos os lados da equação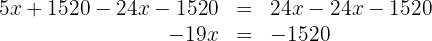
Multiplicamos os dois lados da equação por 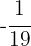
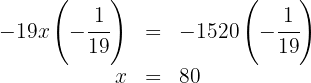
Portanto, a capacidade total do galão é de 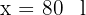
Uma fazenda tem porcos e pavões que somam 35 cabeças e 116 patas. Há, quantos porcos e pavões na fazenda no total?
Vamos chamar de  a quantidade de cabeças de porcos e como no total, há 35 cabeças, então
a quantidade de cabeças de porcos e como no total, há 35 cabeças, então  é o número de cabeças de pavões.
é o número de cabeças de pavões.
Escrevemos a condição das patas, para o qual os porcos têm 4 patas e os pavões 2. Portanto:

Multiplicamos e depois somamos os termos semelhantes:
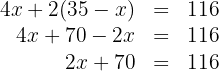
Subtraímos  de ambos os lados da equação
de ambos os lados da equação
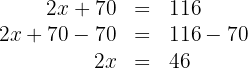
Multiplicamos por  de ambos os lados da equação:
de ambos os lados da equação:
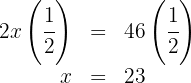
Dessa forma, há 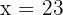 porcos e
porcos e 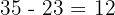 pavões.
pavões.
Luís fez uma viagem de carro, na qual foram consumidos 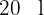 de gasolina. O trajeto foi feito em duas etapas: na primeira, consumiu
de gasolina. O trajeto foi feito em duas etapas: na primeira, consumiu  da gasolina que tinha no tanque e na segunda etapa, a metade da gasolina que sobrou.
da gasolina que tinha no tanque e na segunda etapa, a metade da gasolina que sobrou.
Pergunta-se: qual a quantidade de litros de gasolina que havia no tanque e os litros consumidos em cada etapa?
Vamos chamar de  a quantidade de litros de gasolina que havia no tanque.
a quantidade de litros de gasolina que havia no tanque.
Escrevemos a condição da primeira etapa.

Agora, escrevemos a condição da segunda etapa.
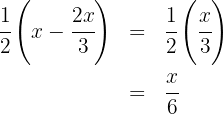
Para encontrar a quantidade de gasolina que havia no tanque, somamos o que foi consumido nas duas etapas, o qual é igual a 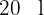
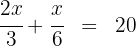
Multiplicamos por  os dois lados da equação
os dois lados da equação
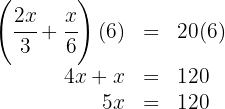
Agora, vamos multiplicar por  de ambos os lados da equação
de ambos os lados da equação
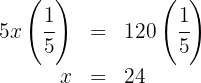
Assim, o tanque tinha  .
.
Na primeira etapa, foram consumidos 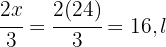 , enquanto na segunda etapa foram consumidos
, enquanto na segunda etapa foram consumidos 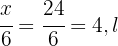
Em uma livraria, Ana compra um livro com um terço de seu dinheiro e um quadrinho com as dois terços do que lhe restou. Ao sair da livraria, ela tinha R$ 12. Quanto dinheiro Ana tinha?
Chamamos de  o total de dinheiro de Ana.
o total de dinheiro de Ana.
Escrevemos a condição do livro.

Agora, escrevemos a condição para o quadrinho.
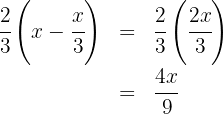
Para encontrar a quantidade de dinheiro que ela tinha, somamos os gastos do livro e do quadrinho com o dinheiro restante:

Multiplicamos por  ambos os lados da equação e somamos os termos semelhantes:
ambos os lados da equação e somamos os termos semelhantes:
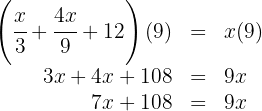
Subtraímos 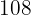 e
e 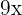 os dois lados da equação
os dois lados da equação
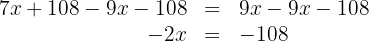
Multiplicamos por  ambos os lados da equação:
ambos os lados da equação:
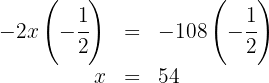
Assim, Ana tinha  R$
R$
Um caminhão parte de uma cidade a uma velocidade de 40 km/h. Uma hora depois, um carro sai da mesma cidade, seguindo na mesma direção e sentido, a uma velocidade de 60 km/h. Determine o tempo necessário para que o carro alcance o caminhão.
Vamos chamar de  o tempo empregado pelo caminhão, logo, o tempo empregado pelo carro é
o tempo empregado pelo caminhão, logo, o tempo empregado pelo carro é 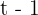
Como ambos os veículos percorrem a mesma distância, podemos estabelecer a seguinte relação:
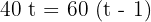
Realizamos a multiplicação:
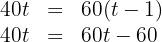
Subtraímos  em ambos os lados da equação:
em ambos os lados da equação:
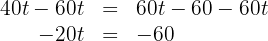
Multiplicamos por 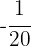 nos dois lados da equação:
nos dois lados da equação:
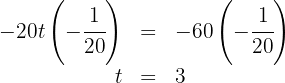
Assim, para que os veículos se encontrem, o caminhão terá percorrido 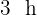 enquanto o carro levará
enquanto o carro levará 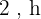
Os dois algarismos de um número são consecutivos, sendo o maior o das dezenas e o menor o das unidades. O número é igual a seis vezes a soma dos seus algarismos. Qual é o número?
Chamamos de  o algarismo das unidades, logo, sendo consecutivos, o algarismo das dezenas é
o algarismo das unidades, logo, sendo consecutivos, o algarismo das dezenas é 
Se temos um número de dois dígitos, por exemplo  , podemos decompor da seguinte forma:
, podemos decompor da seguinte forma:
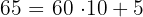
Nosso número de dois dígitos é  , com a condição, vamos obter:
, com a condição, vamos obter:
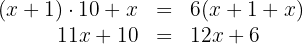
Subtraímos 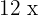 e
e  em ambos os lados da equação:
em ambos os lados da equação:
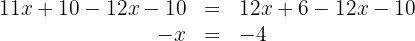
Multiplicamos por  em ambos os lados da equação e obtemos
em ambos os lados da equação e obtemos 
Portanto, o número procurado é:
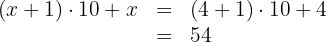
Suponha que você esteja economizando dinheiro para comprar um novo telefone celular que custa R$700. Você tem um trabalho de meio período e ganha R$50 por dia trabalhado. Além disso, recebe uma mesada semanal de R$20 dos seus pais. Você gasta R$3 por cada dia de trabalho. A pergunta é: quantos dias por semana você precisa trabalhar para conseguir comprar o telefone celular em 8 semanas?
Seja  o número de dias que você trabalha por semana. Então, o montante líquido por semana que ganha é de
o número de dias que você trabalha por semana. Então, o montante líquido por semana que ganha é de  . Agora, o que gasta é
. Agora, o que gasta é  semanalmente em transporte e ganha R$20 semanaisde mesada. Então, por semana tem:
semanalmente em transporte e ganha R$20 semanaisde mesada. Então, por semana tem:
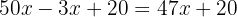
Portanto, em 8 semanas ganha:
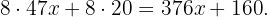
Se, nesse período, precisa de, no mínimo R$700, vamos obter a seguinte equação:

Ou seja, se trabalhar pelo menos 1.7 dias por semana, você pode comprar o celular em 8 semanas.
Uma loja de roupas vende camisetas a um preço fixo de R$15 cada uma. Além disso, a loja cobra uma taxa de envio de R$5 por cada pedido realizado. Um cliente quer comprar um número desconhecido de camisetas e está disposto a gastar no máximo R$80 no total, incluindo o preço das camisetas e o frete.
Quantas camisetas ele pode comprar sem exceder seu orçamento de R$80?
Seja 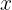 o número de camisetas que o cliente pode comprar. Então, a equação a ser considerada é:
o número de camisetas que o cliente pode comprar. Então, a equação a ser considerada é:
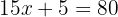
Agora, isolamos a variável:
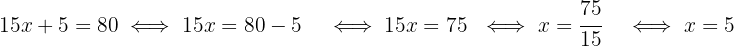
Ou seja, o cliente com um orçamento de R$80 só pode comprar, no máximo, 5 camisetas.
Um estudante trabalha durante o verão para economizar dinheiro para seus gastos escolares. Ele ganha R$8 por hora trabalhada e planeja trabalhar um número desconhecido de horas durante as férias. Além disso, seus gastos escolares somam R$600. O estudante quer saber quantas horas precisa trabalhar para cobrir seus gastos escolares. Quantas horas ele precisa trabalhar? E e ele só puder trabalhar 6 horas por dia, quantos dias deverá trabalhar?
Seja 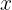 o número de horas que ele deve trabalhar. Então, o dinheiro a ser feito pode ser calculado da seguinte maneira:
o número de horas que ele deve trabalhar. Então, o dinheiro a ser feito pode ser calculado da seguinte maneira:
Dinheiro ganho = (dinheiro por hora) * (horas trabalhadas)
Se ele precisa de R$600, então queremos que o dinheiro ganho seja 600 e devemos isolar a variável horas trabalhadas.
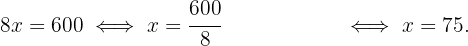
Ou seja, ele deve trabalhar 75 horas para atingir seu objetivo. Agora, se ele só pode trabalhar 6 horas diárias, então ele deve trabalhar por:
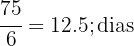
Como deve completar a jornada, portanto, ele deve trabalhar por 13 dias completos.
Uma empresa de envios oferece duas opções de tarifas para o envio de pacotes. A Tarifa A cobra uma taxa fixa de R$10 mais R$2 por cada quilograma de peso do pacote. A Tarifa B, por sua vez, cobra uma taxa fixa de R$15 mais R$1,50 por cada quilograma. Qual deve ser o peso de um pacote para que o custo das duas tarifas seja o mesmo?
Seja 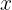 o peso do pacote que queremos enviar. Buscamos um peso tal que:
o peso do pacote que queremos enviar. Buscamos um peso tal que:
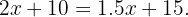
Agora, isolamos a variável peso:
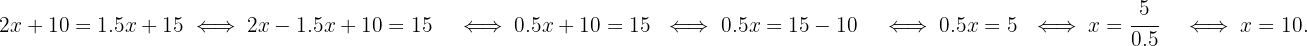
Então, para que ambas as tarifas sejam iguais, o pacote deve pesar 10 kg.
Um cliente está comparando dois planos de telefonia celular. O Plano A tem um custo fixo mensal de R$30, além de R$0,10 por minuto de chamadas. O Plano B, por sua vez, cobra uma taxa fixa mensal de R$45, mais R$0,05 por minuto de chamadas. Quantos minutos o cliente deve utilizar para que o custo de ambos os planos seja o mesmo?
Seja 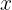 o número de minutos que o cliente utiliza. Então, buscamos uma quantidade de minutos de forma que:
o número de minutos que o cliente utiliza. Então, buscamos uma quantidade de minutos de forma que:
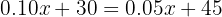
Ou seja, um 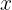 tal que a tarifa de ambos os planos seja igual. Agora, isolamos a variável tempo em minutos:
tal que a tarifa de ambos os planos seja igual. Agora, isolamos a variável tempo em minutos:
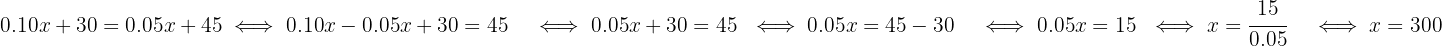
Ou seja, caso o cliente utilize 300 minutos de serviço, o custo das duas tarifas será o mesmo.
Resumir com IA:












