Temas

Sistemas de equações com solução única
Resolva os seguintes sistemas de equações utilizando o método gráfico:
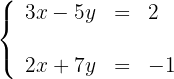
Para desenhar uma reta, basta conhecer dois pontos e traçar a linha que passa por eles.
1 Obtemos dois pontos para cada uma das retas, considerando a interseção com os eixos. Para a primeira reta temos:

Para a primeira reta, os pontos de interseção com os eixos são
Para a segunda reta, os pontos de interseção com os eixos são:

Nós utilizamos a interseção com os eixos como os pontos para construir a reta, mas você pode considerar quaisquer dois valores de  e obter os valores correspondentes de
e obter os valores correspondentes de  ; depois, com uma régua, traça a reta que passa por ambos os pontos. A reta obtida será a mesma que apresentamos.
; depois, com uma régua, traça a reta que passa por ambos os pontos. A reta obtida será a mesma que apresentamos.
2
Representamos os pontos de interseção com os eixos no plano cartesiano e, com a ajuda de uma régua, traçamos ambas as retas e localizamos o ponto de interseção entre elas.

3
A solução do sistema de equações é onde as duas rectas se intersectam, isto é,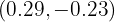 . Observe que, ao substituir essa solução aproximada em ambas as equações, a igualdade não se verifica exatamente:
. Observe que, ao substituir essa solução aproximada em ambas as equações, a igualdade não se verifica exatamente:
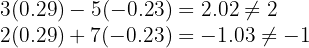
Mas os valores ficam muito próximos; essa é a limitação do método gráfico.
Para obter soluções exatas, utilizam-se métodos analíticos como igualação, redução, substituição, entre outros. Usando os métodos analíticos, a solução exata é:
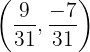
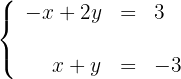
Para desenhar uma reta, basta conhecer dois pontos e traçar a linha que passa por eles.
1
Obtemos dois pontos para cada uma das retas, considerando a interseção com os eixos. Para a primeira reta, temos:

Para a primeira reta, os pontos de interseção com os eixos são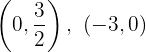
Para a segunda reta, os pontos de interseção com os eixos são:

2
Representamos os pontos de interseção com os eixos no plano cartesiano e, com a ajuda de uma régua, traçamos ambas as retas e localizamos o ponto de interseção entre elas.

3
A solução do sistema de equações é o ponto onde as duas retas se encontram, isto é,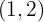 .
.
Observe que, neste caso, ao substituir essa solução nas duas equações, as igualdades são satisfeitas; portanto, a solução obtida é exata:

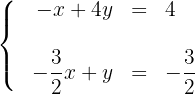
Para desenhar uma reta, basta conhecer dois pontos e traçar a linha que passa por eles.
1
Obtemos dois pontos para cada uma das rectas, considerando a interseção com os eixos. Para a primeira reta temos:

Para a primeira reta, os pontos de interseção com os eixos são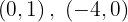
Para a segunda reta, os pontos de interseção com os eixos são:
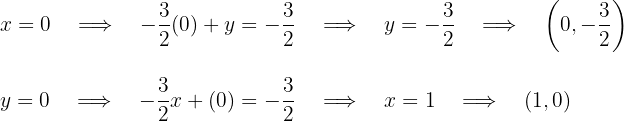
2
Representamos os pontos de interseção com os eixos no plano cartesiano e, com uma régua, traçamos ambas as retas e localizamos o ponto onde elas se intersectam.

3
A solução do sistema de equações é o ponto onde as duas retas se cruzam, isto é: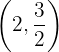 .
.
Observe que, ao substituir essa solução nas duas equações, as igualdades são satisfeitas:

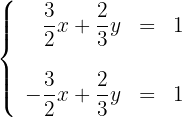
Para desenhar uma reta, basta conhecer dois pontos e traçar a linha que passa por eles.
1
Obtemos dois pontos para cada uma das retas, considerando os valores 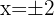 em ambas. Para a primeira reta temos:
em ambas. Para a primeira reta temos:

Para a primeira reta, os pontos obtidos são: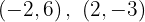
Para a segunda reta, os pontos obtidos são:

2
Representamos os pontos das duas retas no plano cartesiano e, com o auxílio de uma régua, traçamos ambas as retas e localizamos o ponto em que elas se intersectam.

3
A solução do sistema de equações é o ponto onde as duas retas se encontram, isto é: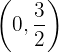 .
.
Observe que, ao substituir essa solução nas duas equações, as igualdades são satisfeitas.
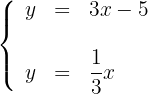
Para desenhar uma reta, basta conhecer dois pontos e traçar a linha que passa por eles.
1
Obtemos dois pontos para cada reta. Considerando os valores 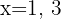 na primeira reta, temos:
na primeira reta, temos:

Para a primeira reta, os pontos obtidos são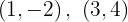
Para a segunda reta, consideramos os valores 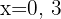 . Os pontos obtidos são:
. Os pontos obtidos são:

2
Representamos os pontos das duas retas no plano cartesiano e, com uma régua, traçamos ambas as retas, localizando o ponto onde elas se intersectam.

3
A solução do sistema de equações é o ponto onde as duas retas se encontram, isto é: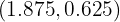 .
.
Observe que, ao substituir essa solução nas duas equações, as igualdades são satisfeitas.
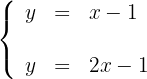
Para desenhar uma reta, basta conhecer dois pontos e traçar a linha que passa por eles.
1
Obtemos dois pontos para cada uma das retas, considerando os valores 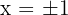 em ambas. Para a primeira reta, temos:
em ambas. Para a primeira reta, temos:

Para a primeira reta, os pontos obtidos são: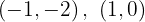
Para a segunda reta, os pontos obtidos são:

2
Representamos os pontos das duas retas no plano cartesiano e, com a ajuda de uma régua, traçamos ambas e identificamos o ponto onde se intersectam.

3
A solução do sistema de equações é o ponto onde as duas retas se encontram, isto é: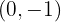 .
.
Observe que, ao substituir essa solução nas duas equações, as igualdades são satisfeitas.
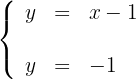
Para desenhar uma reta, basta conhecer dois pontos e traçar a linha que passa por eles.
1
Obtemos dois pontos para cada uma das retas, considerando os valores 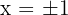 em ambas. Para a primeira reta temos:
em ambas. Para a primeira reta temos:

Para a primeira reta, os pontos obtidos são: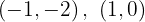
Para a segunda reta, os pontos obtidos são:

2
Representamos os pontos das retas no plano cartesiano e, com a ajuda de uma régua, traçamos ambas as retas e localizamos o ponto onde elas se encontram.

3
A solução do sistema de equações é o ponto onde as duas retas se intersectam, isto é: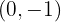 .
.
Observe que, ao substituir essa solução nas duas equações, as igualdades são satisfeitas.
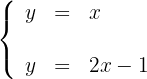
Para desenhar uma reta, basta conhecer dois pontos e traçar a linha que passa por eles.
1
Obtemos dois pontos para cada uma das retas, considerando os valores 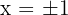 em ambas as retas. Para a primeira reta temos:
em ambas as retas. Para a primeira reta temos:

Para a primeira reta, os pontos obtidos são: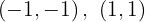
Para a segunda reta, os pontos obtidos são:

2
Representamos os pontos das retas no plano cartesiano e, com a ajuda de uma régua, traçamos ambas as retas e identificamos o ponto de interseção entre elas.

3
A solução do sistema de equações é o ponto onde as duas retas se encontram, isto é: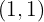 .
.
Observe que, ao substituir essa solução em ambas as equações, as igualdades são satisfeitas.
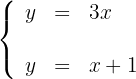
Para desenhar uma reta, basta conhecer dois pontos e traçar a linha que passa por eles.
1
Obtemos dois pontos para cada uma das retas, considerando os valores 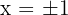 em ambas as equações. Para a primeira reta temos:
em ambas as equações. Para a primeira reta temos:

Para a primeira reta, os pontos obtidos são: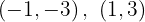
Para a segunda reta, os pontos obtidos são:

2
Representamos os pontos das retas no plano cartesiano e, com a ajuda de uma régua, traçamos ambas as retas para localizar o ponto de interseção.

3
A solução do sistema de equações é o ponto onde as duas retas se encontram, isto é: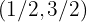 .
.
Observe que, ao substituir essa solução nas duas equações, as igualdades são satisfeitas.
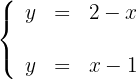
Para desenhar uma reta, basta conhecer dois pontos e traçar a linha que passa por eles.
1
Obtemos dois pontos para cada uma das retas, considerando os valores 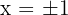 em ambas as equações. Para a primeira reta temos:
em ambas as equações. Para a primeira reta temos:

Para a primeira reta, os pontos obtidos são: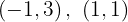
Para a segunda reta, os pontos obtidos são:

2
Representamos os pontos das retas no plano cartesiano e, com a ajuda de uma régua, traçamos ambas as retas para localizar o ponto de interseção.

3
A solução do sistema de equações é o ponto onde as duas retas se encontram, isto é: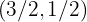 .
.
Observe que, ao substituir essa solução nas duas equações, as igualdades são satisfeitas.
Sistemas de equações sem solução
Resolva os seguintes sistemas de equações utilizando o método gráfico:
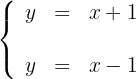
Para desenhar uma reta, basta conhecer dois pontos e traçar a linha que passa por eles.
1
Obtemos dois pontos para cada uma das retas, podemos usar as interseções com os eixos ou escolher valores arbitrários para  e calcular os valores correspondentes de
e calcular os valores correspondentes de  .
.
Neste caso, vamos considerar os valores 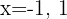 para a primeira reta:
para a primeira reta:

Para a primeira reta, os pontos obtidos são: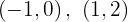
Para a segunda reta, considerando os valores 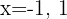 , obtemos:
, obtemos:

2
Representamos os pontos das retas no plano cartesiano e, com a ajuda de uma régua, traçamos ambas as retas e verificamos se existe ponto de interseção.

3
O sistema não possui solução, pois as duas retas são paralelas entre si e não se intersectam, como pode ser observado no gráfico.
Do ponto de vista analítico, ambas as retas têm a mesma inclinação, 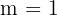 .
.
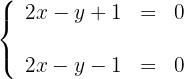
Para desenhar uma reta, basta conhecer dois pontos e traçar a linha que passa por eles.
1
Obtemos dois pontos para cada uma das retas, podemos usar as interseções com os eixos ou escolher valores arbitrários para  e calcular os valores correspondentes de
e calcular os valores correspondentes de  .
.
Nesta ocasião, vamos considerar os valores 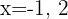 para a primeira reta:
para a primeira reta:

Para a primeira reta, os pontos obtidos são: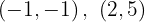
Para a segunda reta, usando os mesmos valores 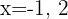 , obtemos:
, obtemos:

2
Representamos os pontos das retas no plano cartesiano e, com o auxílio de uma régua, traçamos ambas as retas para visualizar se existe interseção.

3
O sistema não possui solução, pois as duas retas são paralelas e, portanto, não apresentam ponto de interseção, como pode ser observado no gráfico.
Do ponto de vista analítico, ambas possuem a mesma inclinação, 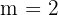 .
.
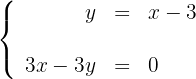
Para desenhar uma reta, basta conhecer dois pontos e traçar a linha que passa por eles.
1
Obtemos dois pontos para cada uma das retas, podemos usar as interseções com os eixos ou escolher valores arbitrários para  e calcular os valores correspondentes de
e calcular os valores correspondentes de  .
.
Nesta ocasião, vamos considerar os valores 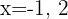 para a primeira reta:
para a primeira reta:

Para a primeira reta, os pontos obtidos são: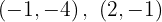
Para a segunda reta, considerando os mesmos valores 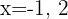 , obtemos:
, obtemos:

2
Representamos os pontos das retas no plano cartesiano e, com o auxílio de uma régua, traçamos ambas as retas para localizar o ponto de interseção.

3
O sistema não possui solução, pois as duas retas são paralelas e, portanto, não apresentam ponto de interseção, como pode ser observado no gráfico.
Do ponto de vista analítico, ambas possuem a mesma inclinação 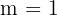 .
.
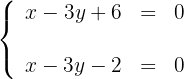
Para desenhar uma reta, basta conhecer dois pontos e traçar a linha que passa por eles.
1
Obtemos dois pontos para cada uma das retas, podemos usar interseções com os eixos ou escolher valores arbitrários para  e calcular os valores correspondentes de
e calcular os valores correspondentes de  .
.
Aqui, consideramos os valores 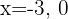 para a primeira reta:
para a primeira reta:

Para a primeira reta, os pontos obtidos são: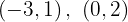
Para a segunda reta, usando os valores 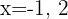 , obtemos:
, obtemos:

2
Representamos os pontos das duas retas no plano cartesiano e, com o auxílio de uma régua, traçamos as linhas para analisar se há interseção.

3
O sistema não possui solução, pois as duas retas são paralelas e não apresentam ponto de interseção, como se observa no gráfico.
Do ponto de vista analítico, ambas possuem a mesma inclinação:
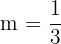 .
.
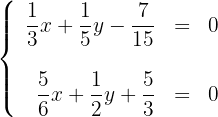
Para desenhar uma reta, basta conhecer dois pontos e traçar a linha que passa por eles.
1
Obtemos dois pontos para cada uma das retas, podemos usar as interseções com os eixos ou escolher valores arbitrários para  e calcular os valores de
e calcular os valores de  .
.
Nesta ocasião, vamos considerar os valores 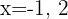 para a primeira reta:
para a primeira reta:

Para a primeira reta, os pontos obtidos são: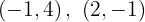
Para a segunda reta, considerando os valores 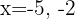 , obtemos:
, obtemos:

2
Representamos os pontos das retas no plano cartesiano e, com o auxílio de uma régua, traçamos ambas as linhas para verificar se existe ponto de interseção.

3
O sistema não possui solução, pois as retas são paralelas e não apresentam ponto de interseção, como pode ser observado no gráfico.
Do ponto de vista analítico, ambas têm a mesma inclinação:
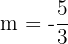 .
.
Sistemas de equações com infinitas soluções
Resolva os seguintes sistemas de equações utilizando o método gráfico:
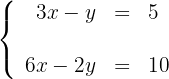
Para desenhar uma reta, basta conhecer dois pontos e traçar a linha que passa por eles.
1
Obtemos dois pontos para cada uma das retas podemos usar as interseções com os eixos ou escolher valores arbitrários para  e calcular os valores correspondentes de
e calcular os valores correspondentes de  .
.
Nesta ocasião, vamos considerar os valores 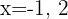 para a primeira reta:
para a primeira reta:

Para a primeira reta, os pontos obtidos são: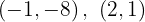
Para a segunda reta, usando os mesmos valores 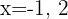 , obtemos:
, obtemos:

2
Representamos os pontos das retas no plano cartesiano e, com o auxílio de uma régua, traçamos ambas as linhas para observar a posição relativa entre elas.

3
Existem infinitas soluções, pois as duas retas são exatamente iguais e coincidem em todos os seus pontos.
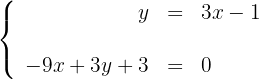
Para desenhar uma reta, basta conhecer dois pontos e traçar a linha que passa por eles.
1
Obtemos dois pontos para cada uma das retas podemos usar as interseções com os eixos ou escolher valores arbitrários para  e calcular os valores correspondentes de
e calcular os valores correspondentes de  .
.
Nesta ocasião, vamos considerar os valores 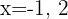 para a primeira reta:
para a primeira reta:

Para a primeira reta, os pontos obtidos são: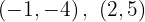
Para a segunda reta, considerando os mesmos valores 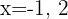 , obtemos:
, obtemos:

2
Representamos os pontos das retas no plano cartesiano e, com o auxílio de uma régua, traçamos ambas as linhas para visualizar o comportamento das duas equações no plano.
3
Existem infinitas soluções, pois as duas retas são exatamente iguais e coincidem em todos os seus pontos.
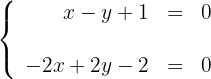
Para desenhar uma reta, basta conhecer dois pontos e traçar a linha que passa por eles.
1
Obtemos dois pontos para cada uma das retas podemos usar as interseções com os eixos ou escolher valores arbitrários para  e calcular os valores correspondentes de
e calcular os valores correspondentes de  .
.
Nesta ocasião, vamos considerar os valores 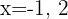 para a primeira reta:
para a primeira reta:

Para a primeira reta, os pontos obtidos são: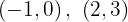
Para a segunda reta, considerando os mesmos valores 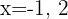 , obtemos:
, obtemos:

2
Representamos os pontos das retas no plano cartesiano e, com o auxílio de uma régua, traçamos ambas as linhas para analisar o comportamento das equações.
3
Existem infinitas soluções, pois as duas retas são exatamente iguais e coincidem em todos os seus pontos.
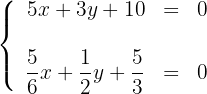
Para desenhar uma reta, basta conhecer dois pontos e traçar a linha que passa por eles.
1
Obtemos dois pontos para cada uma das retas podemos usar as interseções com os eixos ou escolher valores arbitrários para  e calcular os valores de
e calcular os valores de  .
.
Nesta ocasião, vamos considerar os valores 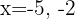 para a primeira reta:
para a primeira reta:

Para a primeira reta, os pontos obtidos são: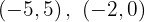
Para a segunda reta, usando os mesmos valores 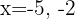 , obtemos:
, obtemos:

2
Representamos os pontos das retas no plano cartesiano e, com auxílio de uma régua, traçamos ambas as linhas para visualizar o comportamento das equações.

3
Existem infinitas soluções, pois as duas retas são exatamente iguais e coincidem em todos os seus pontos.
Se quiser, posso seguir com o próximo exercício.
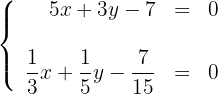
Para desenhar uma reta, basta conhecer dois pontos e traçar a linha que passa por eles.
1
Obtemos dois pontos para cada uma das retas podemos usar as interseções com os eixos ou escolher valores arbitrários para  e calcular os valores correspondentes de
e calcular os valores correspondentes de  .
.
Nesta ocasião, vamos considerar os valores 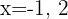 para a primeira reta:
para a primeira reta:

Para a primeira reta, os pontos obtidos são: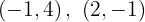
Para a segunda reta, usando os mesmos valores 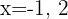 , obtemos:
, obtemos:

2
Representamos os pontos das retas no plano cartesiano e, com o auxílio de uma régua, traçamos ambas as linhas para verificar a posição relativa entre elas.

3
Existem infinitas soluções, pois as duas retas são exatamente iguais e coincidem em todos os seus pontos.
Resumir com IA:












