Bem-vindos à nossa página especializada em exercícios de regressão e correlação! A regressão e a correlação são ferramentas fundamentais na análise de dados, utilizadas em diversas áreas, desde a pesquisa científica até a tomada de decisões empresariais.
Neste artigo, você vai explorar uma variedade de exercícios práticos desenvolvidos para ajudar no entendimento e na aplicação de conceitos-chave relacionados à regressão e correlação. Aqui, você encontrará exemplos claros e desafiadores nos quais deverá encontrar a equação da reta de regressão, calcular o coeficiente de correlação linear, determinar a variância, a covariância e muito mais.
Nesta jornada, você vai aprender a interpretar dados com confiança, descobrir relações importantes entre variáveis e tomar decisões baseadas em evidências. Prepare-se para mergulhar no mundo da regressão e correlação e dominar exercícios que vão transformar sua análise de dados.
A covariância é representada por 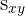 ou
ou  e é dada pelas expressões:
e é dada pelas expressões:
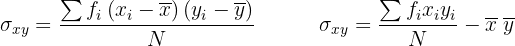
Cinco crianças de 2, 3, 5, 7 e 8 anos pesam, respectivamente, 14, 20, 32, 42 e 44 quilos.
1. Encontre a equação da reta de regressão da idade em função do peso.
2. Qual seria o peso aproximado de uma criança de seis anos?
Cálculo das médias:
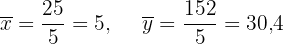
Cálculo da covariância e da variância de  :
:
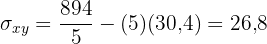
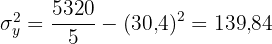
A reta de regressão da idade sobre o peso é aquela que passa pelo ponto  e tem inclinação
e tem inclinação  :
:
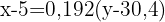
Isolando  , obtemos a reta de regressão:
, obtemos a reta de regressão:
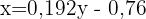
Para estimar o peso aproximado de uma criança de seis anos, substituímos 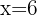 na equação de regressão, resultando em:
na equação de regressão, resultando em:
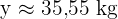
 |  | 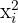 |  |  |
|---|---|---|---|---|
 |  |  |  |  |
 |  |  |  |  |
 |  |  | 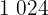 |  |
 |  |  |  | 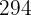 |
 |  |  |  | 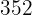 |
 | 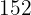 | 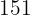 |  | 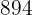 |
Um shopping observou que o número de clientes (em centenas) varia de acordo com a distância (em km) de um núcleo populacional, conforme os dados da tabela:
Nº de Clientes 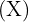 | Distância 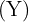 |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
1. Calcule o coeficiente de correlação linear.
2. Se o shopping estiver a  km de distância, quantos clientes (em centenas) pode esperar?
km de distância, quantos clientes (em centenas) pode esperar?
3. Se desejar receber  clientes (em centenas), a que distância do núcleo populacional deve se situar?
clientes (em centenas), a que distância do núcleo populacional deve se situar?
Calculamos as médias:
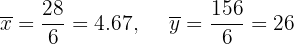
Calculamos a covariância, as variâncias e os desvios padrão:
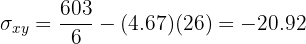
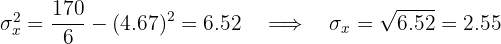
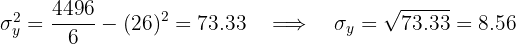
O coeficiente de correlação é dado por:

Observa-se uma correlação negativa muito forte.
A reta de regressão dos clientes sobre a distância é aquela que passa pelo ponto  e tem inclinação
e tem inclinação  :
:
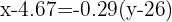
Isolando  , obtemos a reta de regressão:
, obtemos a reta de regressão:
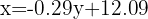
Para encontrar o número de clientes quando o shopping está a 2 km:
Substituímos  na equação de regressão:
na equação de regressão:
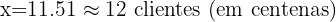
Para receber 5 clientes (em centenas):
Substituímos  na equação:
na equação:
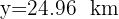
 |  |  | 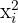 |  |
|---|---|---|---|---|
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  | 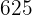 |
 |  |  |  | 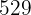 |
 |  |  |  | 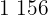 |
 |  |  |  | 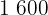 |
 |  |  |  |  |
As notas obtidas por cinco alunos em matemática e química foram:
| Matemática | Química |
 |  |
 |  |
 |  |
 |  |
 |  |
Determine as retas de regresão e calcule a nota esperada em química para um aluno que tirou  em matemática.
em matemática.
Calculamos as médias:
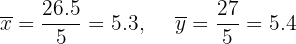
Calculamos a covariância e a variância de  :
:
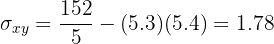
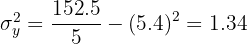
A reta de regressão da nota de matemática sobre a nota de química é aquela que passa pelo ponto  e tem inclinação
e tem inclinação  :
:
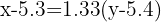
Isolamos e obtemos a reta de regressão:
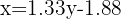
Desta mesma equação, isolamos  e obtemos a reta de regressão em termos da nota em matemática:
e obtemos a reta de regressão em termos da nota em matemática:

Para encontrar a nota esperada em química para um aluno que tem sete ponto cinco em matemáticas, substituímos 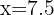 na equação de regressão e obtemos:
na equação de regressão e obtemos:
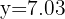
 |  | 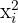 |  |  |
|---|---|---|---|---|
 |  |  | 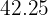 |  |
 |  |  |  |  |
 |  |  |  | 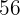 |
 |  |  |  |  |
 |  | 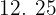 |  |  |
 |  | 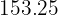 | 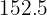 | 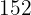 |
Um conjunto de dados bidimensional  tem coeficiente de correlação
tem coeficiente de correlação  , sendo as médias das distribuições marginais
, sendo as médias das distribuições marginais 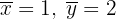 . abe-se que uma das quatro equações seguintes corresponde à reta de regressão de
. abe-se que uma das quatro equações seguintes corresponde à reta de regressão de  sobre
sobre  :
:
1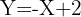
2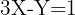
3
4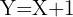
Escolha a reta correta.
Como o coeficiente de correlação linear é negativo, a inclinação da reta também será negativa, portanto descartamos  e
e  .
.
Um ponto da reta deve ser  , ou seja,
, ou seja,  . Substituímos em 1 e 3 para ver qual satisfaz a igualdade:
. Substituímos em 1 e 3 para ver qual satisfaz a igualdade:
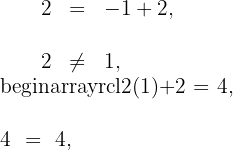
A reta pedida é a 3.
A estatura e peso de  jogadores de um time de basquete são:
jogadores de um time de basquete são:
Estatura  | Peso  |
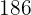 |  |
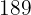 |  |
 |  |
 |  |
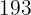 |  |
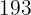 |  |
 |  |
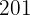 | 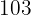 |
 |  |
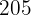 |  |
Calcule:
1 A reta de regressão de  sobre
sobre  .
.
2 O coeficiente de correlação.
3 O peso estimado de um jogador que mede 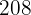 cm.
cm.
Calculamos as médias:
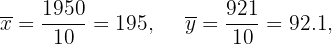
Calculamos a covariância, variância e os devios padrão:

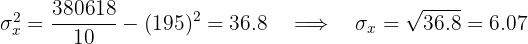
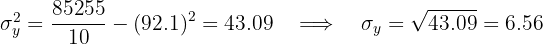
O coeficiente de correlação é dado por 
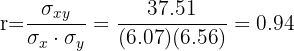
Tem uma correlação positiva muito forte.
A reta de regressão dos pesos em relação à estatura, é a que pssa pelo ponto  e tem inclinação
e tem inclinação
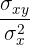
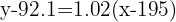
Isolamos e obtemos a reta de regressão:

Para encontrar o peso de um jogador que mede 208 cm, substituimos 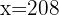 na equação de regressão e obtemos:
na equação de regressão e obtemos:
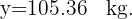
 | 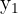 | 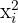 |  |  |
|---|---|---|---|---|
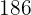 |  | 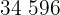 | 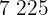 | 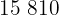 |
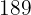 |  | 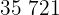 | 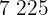 | 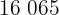 |
 |  | 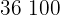 |  |  |
 |  | 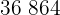 | 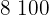 | 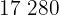 |
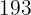 |  |  |  |  |
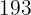 |  |  | 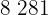 |  |
 |  |  | 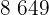 |  |
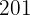 | 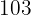 |  |  |  |
 |  | 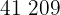 |  | 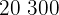 |
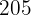 |  |  | 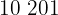 |  |
 |  |  | 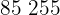 | 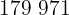 |
De acordo com as informações referentes às horas trabalhadas em uma oficina  e às unidades produzidas
e às unidades produzidas  , determine a reta de regressão de
, determine a reta de regressão de  em relação à
em relação à  , o coeficiente de correlação linear e interprete os dados obtidos.
, o coeficiente de correlação linear e interprete os dados obtidos.
Horas  | Produção  |
 |  |
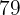 |  |
 |  |
 |  |
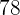 |  |
 | 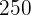 |
 |  |
 | 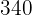 |
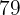 |  |
 |  |
 | 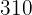 |
 |  |
Cálculo das médias:
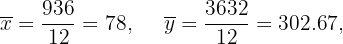
Calculamos a covariância, variância e os devios padrão:
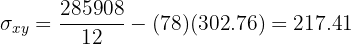

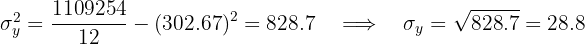
O coeficiente de correlação é dado por 
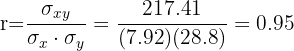
Tem uma correlação positiva muito forte.
A reta de regressão de  em relação à
em relação à  , passa pelo ponto
, passa pelo ponto  e tem inclinação:
e tem inclinação:
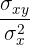

Isolamos e obtemos a reta de regressão:
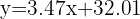
 |  | 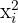 |  |  |
|---|---|---|---|---|
 |  | 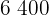 |  |  |
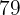 |  |  |  |  |
 |  | 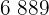 | 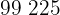 |  |
 |  | 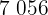 |  | 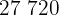 |
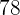 |  | 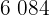 |  |  |
 | 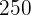 | 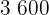 | 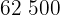 |  |
 |  | 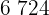 |  | 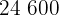 |
 | 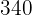 | 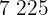 | 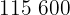 |  |
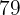 |  |  | 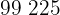 | 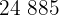 |
 |  | 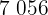 |  | 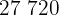 |
 | 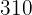 | 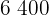 |  | 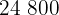 |
 |  | 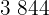 | 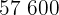 |  |
 | 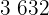 | 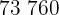 | 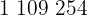 |  |
Solicitaram a um grupo de  pessoas, informações o número de horas que dedicam, diariamente, ao sono e a ver televisão. E de acordo com as respostas, foi elaborada a seguinte tabela:
pessoas, informações o número de horas que dedicam, diariamente, ao sono e a ver televisão. E de acordo com as respostas, foi elaborada a seguinte tabela:
Nº de horas dormidas  |  |  |  |  |  |
Nº de horas de televisão  |  |  |  |  |  |
Frequências absolutas 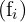 |  |  |  |  |  |
Pede-se para:
1Calcular o coeficiente de correlação.
2Determinar a equação da reta de regressão de  em relação a
em relação a  .
.
3Se uma pessoa dorme 8 horas e meia, quantas horas são estimadas de televisão?
Calculamos as médias:
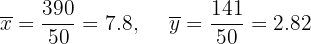
Calculamos a covariância, as variâncias e os desvios padrão:
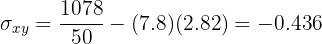
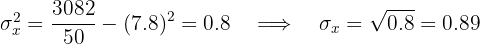

O coeficiente de correlação é dado por:

Observa-se uma correlação negativa e forte.
A reta de regressão de  sobre
sobre  é aquela que passa pelo ponto
é aquela que passa pelo ponto  e tem inclinação
e tem inclinação 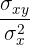 :
:
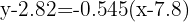
Isolando y, obtemos a reta de regressão:
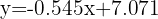
Para estimar o número de horas de televisão para quem dorme 8.5 horas:
Substituindo 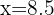 na equação:
na equação:
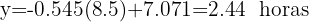
 |  |  | 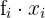 |  | 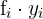 | 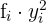 |  |
|---|---|---|---|---|---|---|---|
 |  |  |  | 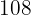 |  |  |  |
 |  |  | 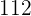 |  |  |  | 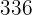 |
 |  |  |  |  |  | 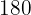 |  |
 |  |  |  | 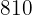 |  |  | 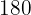 |
 |  |  |  |  |  |  |  |
 | 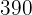 |  | 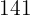 | 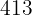 |  |
A tabela a seguir apresenta as notas do teste de aptidão  aplicado a seis vendedores em período de experiência, juntamente com suas respectivas vendas no primeiro mês
aplicado a seis vendedores em período de experiência, juntamente com suas respectivas vendas no primeiro mês  (valores expressos em centenas de euros).
(valores expressos em centenas de euros).
 |  |  |  |  |  |  |
 |  |  |  |  |  |  |
1 Calcule o coeficiente de correlação e interpretar o resultado obtido.
2 Calcule a reta de regressão de  em relação a
em relação a  .
.
3 Faça a estimativa de vendas de um vendedor que obtenha  no teste.
no teste.
Calculamos as médias:
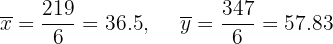
Calculamos a covariância, as variâncias e os desvios padrão:

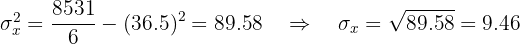
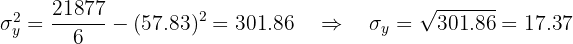
O coeficiente de correlação é dado por:
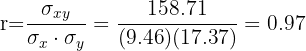
Observa-se uma correlação positiva muito forte.
A reta de regressão de  sobre
sobre  é aquela que passa pelo ponto
é aquela que passa pelo ponto  e tem inclinação
e tem inclinação 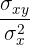 :
:

Isolando y, obtemos a reta de regressão:
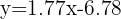
Para estimar as vendas de um vendedor com nota 47 no teste, substituindo  na equação:
na equação:
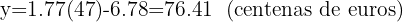
 | 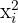 |  |  | |
|---|---|---|---|---|
 |  | 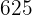 |  | 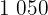 |
 |  |  | 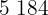 | 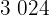 |
 |  | 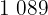 |  |  |
 |  | 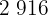 | 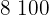 |  |
 |  | 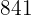 | 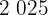 | 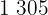 |
 |  | 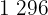 | 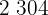 | 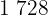 |
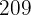 | 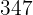 | 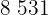 | 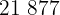 |  |
A tabela abaixo mostra a relação entre a temperatura média mensal (T) em 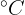 de uma cidade específica e as vendas mensais de sorvete em milhares de reais (R).
de uma cidade específica e as vendas mensais de sorvete em milhares de reais (R).
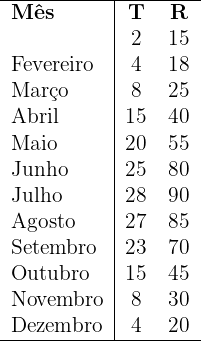
1. Encontre a reta de regressão das vendas mensais em função da temperatura média de cada mês.
2. Calcule o coeficiente de correlação linear e interprete o resultado.
3. Usando a reta de regressão, quantos milhares de reais seriam vendidos em um mês com temperatura média de 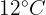 ?
?
4. Segundo este modelo, faria sentido para uma sorveteria local investir 5 mil reais em um mês com temperatura média de 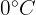 ?
?
1 Queremos encontrar números reais  e
e  de forma que poderemos escrever
de forma que poderemos escrever  se aproxime da melhor forma à reta
se aproxime da melhor forma à reta 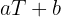 . Assim, primeiro, calculamos a soma dos dados
. Assim, primeiro, calculamos a soma dos dados 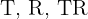 e
e 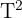 .
.
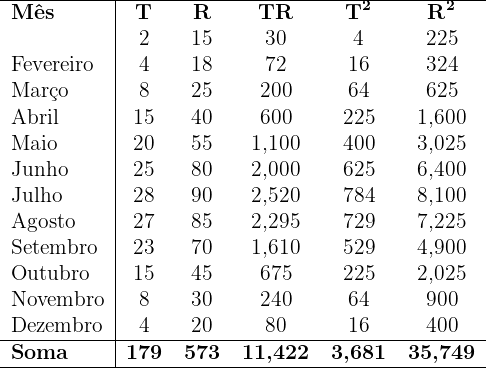
Agora calculamos as médias, a covariância e os desvios padrão:

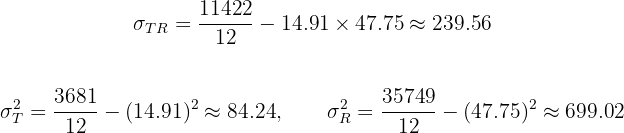
Ou seja,

Portanto, concluimos que
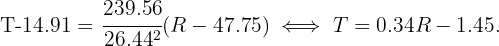
2 O coeficiente de correlação linear é dado por:

Ou seja, a venda mensal de sorvete tem uma correlação forte positiva com a temperatura média de cada mês.
3Queremos isolar para  na equação
na equação
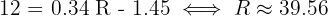
Então, 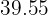 é a reta de regressão é esperada em um mês em que a temperatura média é de
é a reta de regressão é esperada em um mês em que a temperatura média é de 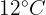 .
.
4 De acordo com a reta de regressão, a venda de sorvete em um mês com esta temperatura seria de 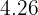 mil reais. Isso significa que, qualquer investimento acima desse valor, levaria a prejuízo. Dessa forma, não seria interessante para o negócio aplicar os 5 mil reais nessa situação.
mil reais. Isso significa que, qualquer investimento acima desse valor, levaria a prejuízo. Dessa forma, não seria interessante para o negócio aplicar os 5 mil reais nessa situação.
A tabela abaixo mostra a relação entre o nível máximo de escolaridade de um indivíduo e a probabilidade de estar em determinada faixa de renda anual (em milhares de dólares):
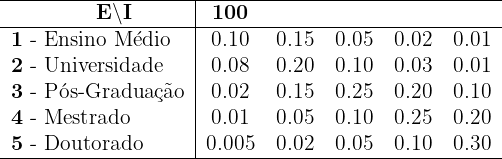
1 Calcule a covariância, o desvio padrão e as médias
2Determine o coeficiente de correlação.
1Convertemos a tabela dada para uma simples. Representaremos o intervalo  como
como  e os demais intervalos serão representados pela média dos pontos limite.
e os demais intervalos serão representados pela média dos pontos limite.
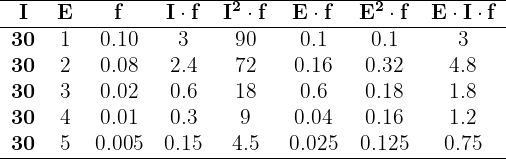
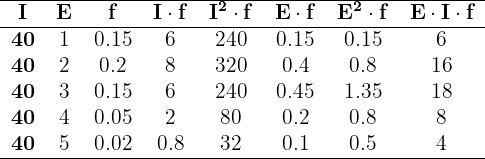
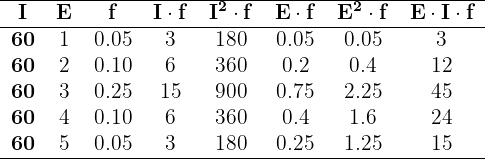
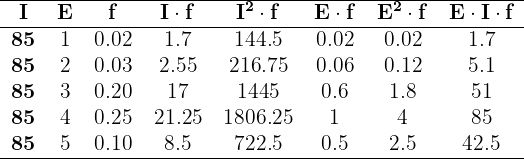
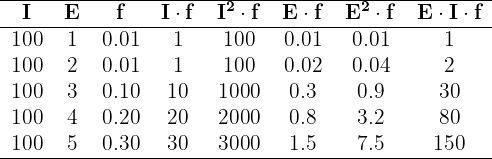
Somando todos os valores das colunas necessárias, temos:
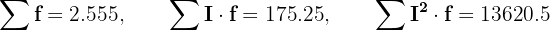

Além disso, obtemos:


e a covariância é:
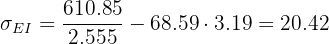
2
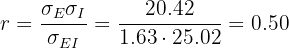
Ou seja, existe uma correlação moderada.


