As raízes quadradas são uma ferramenta fundamental na matemática que nos permite encontrar o valor de um número que, ao ser multiplicado por ele mesmo, produz um resultado igual ao número original. Saber como obter raízes quadradas passo a passo é essencial para resolver uma variedade de problemas em diferentes áreas: da geometria à física e à engenharia.
O processo de encontrar uma raiz quadrada pode parecer complexo no início, mas seguindo uma sequência de passos claro e metodológico, podemos simplificá-lo e torná-lo acessível para todos. A seguir, vamos te guiar por um método passo a passo que permitirá calcular raízes quadradas com confiança e precisão.
Calcule as raízes quadradas dos seguintes valores:
264
1Separamos os algarismos em grupos de dois, começando pela direita.

3Subtraímos o quadrado obtido do primeiro grupo.
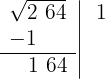
4 Atrás do resto colocamos o grupo seguinte de algarismos do radicando (64), separamos do número formado o último algarismo à direita (4) e dividimos o que resta (16) pelo dobro do número que temos na raiz, isto é, 2·1 = 2.
Abaixo da raiz colocamos outra com o dobro obtido (2), seguido do quociente da divisão (8), e o número formado é multiplicado por esse quociente (8).
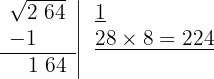
5 Como esse número é maior que o resto (164), precisamos testar números menores até que o produto seja menor que o resto. Com 6, o resultado é menor que o resto, portanto colocamos 6 como 2º algarismo da raiz.
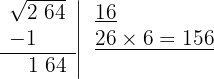
6 Subtraímos o produto obtido (156) do resto (164).
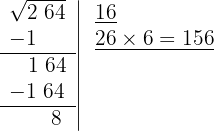
7 Significa que 16 é a raiz e 8 é o resto. O processo fornece soluções inteiras, isto é, encontra o quadrado mais próximo, pela esquerda, de 264, isto é, 16², e determina a quantidade necessária para chegar ao número em questão, 8.
8 Verificamos o resultado:
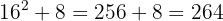
351
segue sem dar. nao tenho plugin.
1Separamos os algarismos em grupos de dois, começando pela direita.

2Com o primeiro grupo calculamos o número cujo quadrado é imediatamente inferior.

3O quadrado do número obtido é subtraído do primeiro grupo.
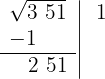
4 Atrás do resto colocamos o grupo seguinte do radicando (51), separamos do número formado o último algarismo à direita (1) e dividimos o que resta (25) pelo dobro do número que temos na raiz, isto é, 2·1 = 2.
O quociente da divisão é maior que 10, por isso escolhemos 9; abaixo da raiz colocamos outra com o dobro obtido (2), seguido do quociente (9), e o número formado é multiplicado por esse quociente (9).
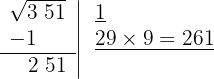
5 Como esse número é maior que o resto (251), precisamos testar números menores até que o produto seja menor que o resto. Com 8 o resultado é menor que o resto, portanto colocamos 8 como 2º algarismo da raiz.
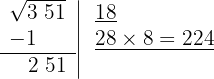
6 Subtraímos o produto obtido (224) do resto (251).
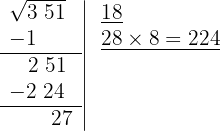
7 Significa que 18 é a raiz e 27 é o resto. O processo fornece soluções inteiras, isto é, encontra o quadrado mais próximo, pela esquerda, de 351, isto é, 18², e determina a quantidade necessária para chegar ao número em questão, 27.
8 Verificamos o resultado:
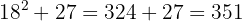
721
1Separamos os algarismos em grupos de dois, começando pela direita.

2Com o primeiro algarismo (7) calculamos o número cujo quadrado é imediatamente inferior.
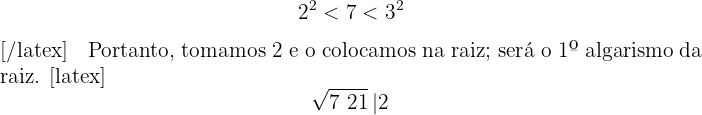
3O quadrado do número obtido é subtraído do primeiro grupo.
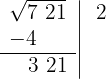
4 Atrás do resto colocamos o grupo seguinte do radicando (21), separamos do número formado o último algarismo à direita (1) e dividimos o que resta (32) pelo dobro do número que temos na raiz, isto é, 2·2 = 4.
Abaixo da raiz colocamos outra com o dobro obtido (4), seguido do quociente da divisão (8), e o número formado é multiplicado por esse quociente (8).
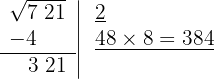
5 Como esse número é maior que o resto (321), precisamos testar números menores até que o produto seja menor que o resto. Com 6 o resultado é menor que o resto, portanto colocamos 6 como 2º algarismo da raiz.
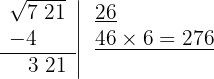
6 Subtraímos o produto obtido (276) do resto (321).
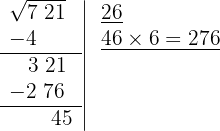
7 Significa que 26 é a raiz e 45 é o resto. O processo fornece soluções inteiras, isto é, encontra o quadrado mais próximo, pela esquerda, de 721, isto é, 26², e determina a quantidade necessária para chegar ao número em questão, 45.
8 Verificamos o resultado:
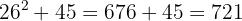
999
1Separamos os algarismos em grupos de dois, começando pela direita.

2Com o primeiro algarismo (9) calculamos o número cujo quadrado é imediatamente inferior.
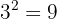
Portanto, tomamos 3 e o colocamos na raiz; será o 1º algarismo da raiz.
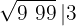
3O quadrado do número obtido é subtraído do primeiro grupo.
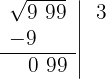
4 Atrás do resto colocamos o grupo seguinte do radicando (99), separamos do número formado o último algarismo à direita (9) e dividimos o que resta (9) pelo dobro do número que temos na raiz, isto é, 2·3 = 6.
Abaixo da raiz colocamos outra com o dobro obtido (6), seguido do quociente da divisão (1), e o número formado é multiplicado por esse quociente (1).
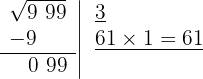
5 Como esse número é menor que o resto (99), colocamos 1 como 2º algarismo da raiz.
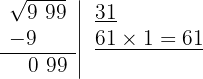
6 Subtraímos o produto obtido (61) do resto (99).
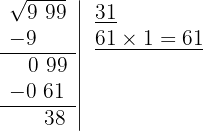
7 Significa que 31 é a raiz e 38 é o resto. O processo fornece soluções inteiras, isto é, encontra o quadrado mais próximo, pela esquerda, de 999, isto é, 31², e determina a quantidade necessária para chegar ao número em questão, 38.
8 Verificamos o resultado:

6256
1Separamos os algarismos em grupos de dois, começando pela direita.
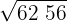
2Com o primeiro algarismo (62) calculamos o número cujo quadrado é imediatamente inferior.
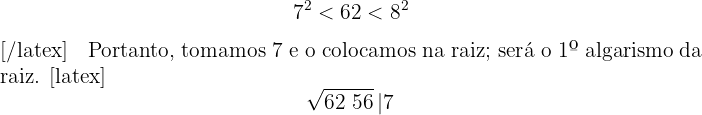
3O quadrado do número obtido é subtraído do primeiro grupo.

4 Atrás do resto colocamos o grupo seguinte do radicando (56), separamos do número formado o último algarismo à direita (6) e dividimos o que resta (135) pelo dobro do número que temos na raiz, isto é, 2·7 = 14.
O quociente da divisão é 9; abaixo da raiz colocamos outra com o dobro obtido (14), seguido do quociente (9), e o número formado é multiplicado por esse quociente (9).
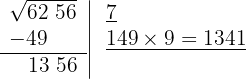
5 Como esse número é menor que o resto (1356), colocamos 9 como 2º algarismo da raiz.
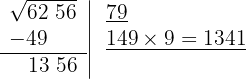
6 Subtraímos o produto obtido (1341) do resto (1356).
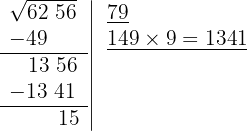
7 Significa que 79 é a raiz e 15 é o resto. O processo fornece soluções inteiras, isto é, encontra o quadrado mais próximo, pela esquerda, de 6256, isto é, 79², e determina a quantidade necessária para chegar ao número em questão, 15.
8 Verificamos o resultado:

8900
1Separamos os algarismos em grupos de dois, começando pela direita.
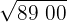
2Com o primeiro algarismo (89) calculamos o número cujo quadrado é imediatamente inferior.

3O quadrado do número obtido é subtraído do primeiro grupo.

4 Atrás do resto colocamos o grupo seguinte do radicando (00), separamos do número formado o último algarismo à direita (0) e dividimos o que resta (80) pelo dobro do número que temos na raiz, isto é, 2·9 = 18.
O quociente da divisão é 4; abaixo da raiz colocamos outra com o dobro obtido (18), seguido do quociente (4), e o número formado é multiplicado por esse quociente (4).
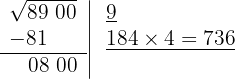
5 Como esse número é menor que o resto (800), colocamos 4 como 2º algarismo da raiz.
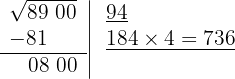
6 Subtraímos o produto obtido (736) do resto (800).
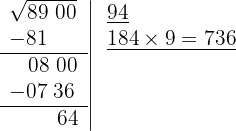
7 Significa que 94 é a raiz e 64 é o resto. O processo fornece soluções inteiras, isto é, encontra o quadrado mais próximo, pela esquerda, de 8900, isto é, 94², e determina a quantidade necessária para chegar ao número em questão, 64.
8 Verificamos o resultado:

72675
1Separamos os algarismos em grupos de dois, começando pela direita.
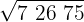
2Com o primeiro algarismo (7) calculamos o número cujo quadrado é imediatamente inferior.

3O quadrado do número obtido é subtraído do primeiro grupo.
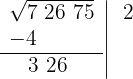
4 Atrás do resto colocamos o grupo seguinte do radicando (26), separamos do número formado o último algarismo à direita (6) e dividimos o que resta (32) pelo dobro do número que temos na raiz, isto é, 2·2 = 4.
O quociente da divisão é 8; abaixo da raiz colocamos outra com o dobro obtido (4), seguido do quociente (8), e o número formado é multiplicado por esse quociente (8).
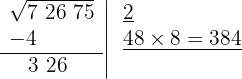
5 Como esse número é maior que o resto (326), precisamos testar números menores até que o produto seja menor que o resto. Com 6 o resultado é menor que o resto, portanto colocamos 6 como 2º algarismo da raiz.
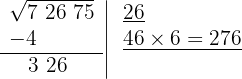
6 Subtraímos o produto obtido (276) do resto (326).
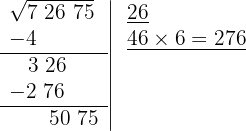
7 Atrás do resto colocamos o grupo seguinte do radicando (75), separando do número formado o último algarismo à direita (5), e dividimos o que resta (507) pelo dobro do número que temos na raiz, isto é, 2·26 = 52.
O quociente da divisão é 9; abaixo da raiz colocamos outra com o dobro obtido (52), seguido do quociente (9), e o número formado é multiplicado por esse quociente (9).
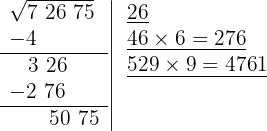
8 Como esse número é menor que o resto (5075), colocamos 9 como 3º algarismo da raiz.
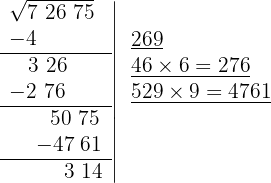
9 Significa que 269 é a raiz e 314 é o resto. O processo fornece soluções inteiras, isto é, encontra o quadrado mais próximo, pela esquerda, de 72675, isto é, 269², e determina a quantidade necessária para chegar ao número em questão, 314.
10 Verificamos o resultado:
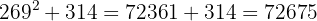
99875
1Separamos os algarismos em grupos de dois, começando pela direita.
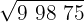
2Com o primeiro algarismo (9) calculamos o número cujo quadrado é imediatamente inferior.
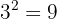
Portanto, tomamos 3 e o colocamos na raiz; será o 1º algarismo da raiz.
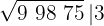
3O quadrado do número obtido é subtraído do primeiro grupo.
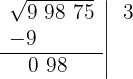
4 Atrás do resto colocamos o grupo seguinte do radicando (98), separamos do número formado o último algarismo à direita (8) e dividimos o que resta (9) pelo dobro do número que temos na raiz, isto é, 2·3 = 6.
O quociente da divisão é 1; abaixo da raiz colocamos outra com o dobro obtido (6), seguido do quociente (1), e o número formado é multiplicado por esse quociente (1).
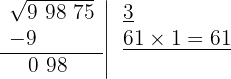
5 Como esse número é menor que o resto (98), colocamos 1 como 2º algarismo da raiz.
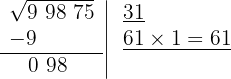
6 Subtraímos o produto obtido (61) do resto (98).
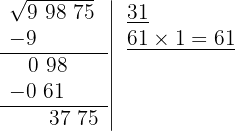
7 Atrás do resto colocamos o grupo seguinte do radicando (75), separando do número formado o último algarismo à direita (5), e dividimos o que resta (377) pelo dobro do número que temos na raiz, isto é, 2·31 = 62.
O quociente da divisão é 6; abaixo da raiz colocamos outra com o dobro obtido (62), seguido do quociente (6), e o número formado é multiplicado por esse quociente (6).
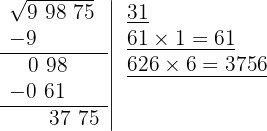
8 Como esse número é menor que o resto (3775), colocamos 6 como 3º algarismo da raiz.
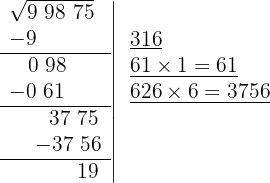
9 Significa que 316 é a raiz e 19 é o resto. O processo fornece soluções inteiras, isto é, encontra o quadrado mais próximo, pela esquerda, de 99875, isto é, 316², e determina a quantidade necessária para chegar ao número em questão, 19.
10 Verificamos o resultado:
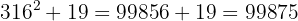
264.315
1 Separamos os algarismos em grupos de dois, começando pela direita, de modo que as casas decimais fiquem em grupos de dois.
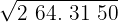
2Com o primeiro algarismo (2) calculamos o número cujo quadrado é imediatamente inferior.
3O quadrado do número obtido é subtraído do primeiro grupo.

4 Atrás do resto colocamos o grupo seguinte do radicando (64), separamos do número formado o último algarismo à direita (4) e dividimos o que resta (16) pelo dobro do número que temos na raiz, isto é, 2·1 = 2.
O quociente da divisão é 8; abaixo da raiz colocamos outra com o dobro obtido (2), seguido do quociente (8), e o número formado é multiplicado por esse quociente (8).
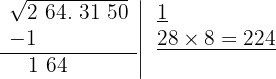
5 Como esse número é maior que o resto (164), precisamos testar números menores até que o produto seja menor que o resto. Com 6 o resultado é menor que o resto, portanto colocamos 6 como 2º algarismo da raiz.
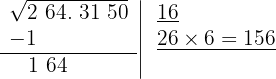
6 Subtraímos o produto obtido (156) do resto (164).

7Atrás do resto colocamos o grupo seguinte do radicando (31), separando do número formado o último algarismo à direita (1), e dividimos o que resta (83) pelo dobro do número que temos na raiz, isto é, 2·16 = 32.
O quociente da divisão é 2; abaixo da raiz colocamos outra com o dobro obtido (32), seguido do quociente (2), e o número formado é multiplicado por esse quociente (2).
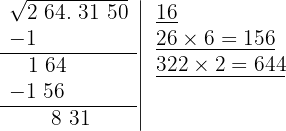
8 Como esse número é menor que o resto (831), colocamos 2 como 3º algarismo da raiz, antecipando um ponto, já que o grupo 31 pertence às casas decimais.
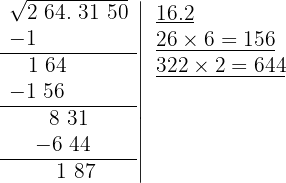
9 Atrás do resto colocamos o grupo seguinte do radicando (50), separando do número formado o último algarismo à direita (0), e dividimos o que resta (1875) pelo dobro do número que temos na raiz sem o ponto decimal, isto é, 2·162 = 324.
O quociente da divisão é 5; abaixo da raiz colocamos outra com o dobro obtido (324), seguido do quociente (5), e o número formado é multiplicado por esse quociente (5).
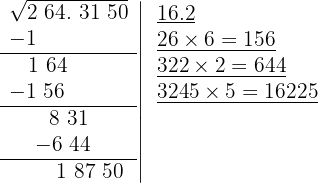
10 Como esse número é menor que o resto (18750), colocamos 5 como 4º algarismo da raiz.
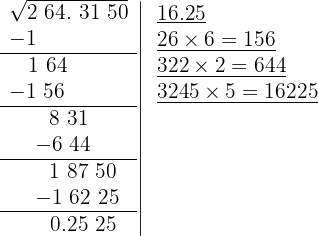
11Significa que 16,25 é a raiz e 0,2525 é o resto.
72675.687
Seguindo os passos dos exercícios anteriores, obtém-se:

Significa que 269,58 é a raiz e 2,3106 é o resto.
Resumir com IA:


