Temas
Sejam bem-vindos à nossa seção de Exercícios de Progressões Geométricas. As progressões geométricas são uma área fascinante da matemática, presente em diversos contextos, desde o crescimento exponencial até os cálculos financeiros. Ao longo desta seção, apresentaremos soluções detalhadas para uma variedade de problemas que envolvem progressões geométricas, com o objetivo de fortalecer sua compreensão e suas habilidades nesse tema.
Cada exercício resolvido é apresentado de forma clara e sistemática, conduzindo passo a passo pelo processo de resolução. Exploraremos conceitos como o termo geral, a soma dos termos e outras propriedades fundamentais das progressões geométricas. Esses exercícios não apenas auxiliam na compreensão da teoria, como também fornecem ferramentas práticas para enfrentar problemas do mundo real que envolvem esse tipo de progressão.
Convidamos você a se aprofundar nesses exercícios resolvidos, aproveitando a oportunidade para consolidar seus conhecimentos e aplicar as progressões geométricas de forma eficaz em diferentes situações matemáticas e práticas.
Exercícios
O 2º termo de uma progressão geométrica é 
, e o 5º é 
. Escreva a progressão.
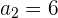
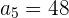
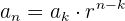
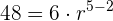
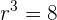
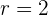
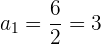
O 1º termo de uma progressão geométrica é 
, e o 8º é 
. Determine a razão, e a soma e o produto dos 8 primeiros termos.
;
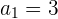
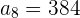Calculando a razão
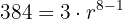
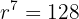
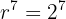
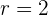
Soma de n- termos:
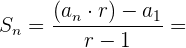
Produto de n-termos:
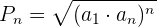
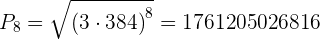
Interpole três meios geométricos entre e .
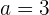
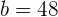
Calculando la razón:
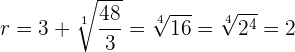
Escribir los términos:
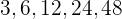
Calcule a soma dos primeiros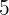 
termos da progressão:
Calcule a soma dos 5 termos da progressão geométrica decrescente ilimitada:
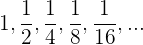
Calculamos a razão :
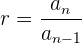
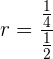
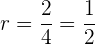
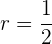
Usamos a formula para a soma de n termos.
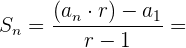
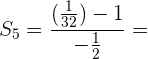
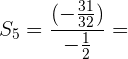
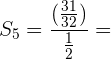
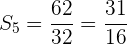
Calcule o produto dos primeiros 5 termos da progressão:
Usamos a fórmula para o produto de n termos:
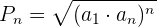
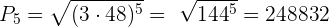
João comprou 20 livros. Pelo 1º pagou R$1,00, pelo 2º, R$2,00, pelo 3º, R$4,00, pelo 4º R$8,00 e assim. sucessivamente. Quanto João pagou pelos livros?
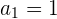
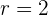
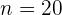
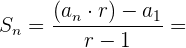
Calculamos o número termo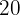 
:
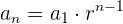
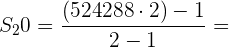
Unindo os pontos médios dos lados de um quadrado de lado 
, obtém-se outro, no qual repetimos a mesma operação e assim, continua indefinidamente. Calcule a soma das áreas dos infinitos quadrados.
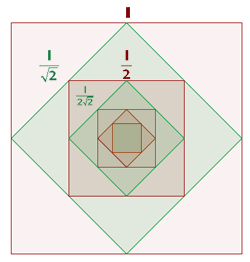
É através do Teorema de Pitágoras que podemos calcular o segundo termo da sucessão:
Tendo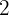 
termos, podemos calcular a razão:
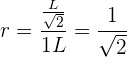
A sucessão é:
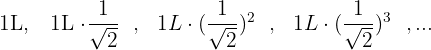
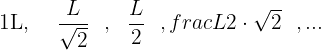
Elevamos cada termo ao quadrado para poder visualizar a progressão de uma forma mais simples:
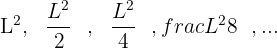
Aplicamos a formula para a soma de n termos, usando o conceito de limite, lembramos que quando n tende a infinito no denominador, o valor da fração tende a zero.
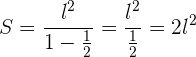
Determine a fração geratriz de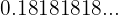 
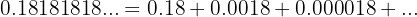
É uma progressão geométrica decrescente ilimitada.
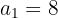
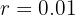
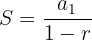
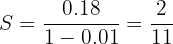
Encontre a fração geratriz de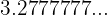 
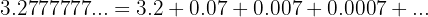
Temos uma progressão geométrica decrescente ilimitada
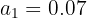
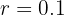
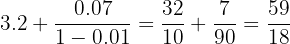
Encontre a fração geratriz do número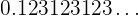 
O número pode ser representado da forma:
Suponha que um investimento inicial de R$5000,00 com uma taxa de juros fixa de 8% ao mês. Quanto valerá o investimento depois de 10 meses se os rendimentos forem reinvestidos em uma progressão geométrica?
Para um investimento inicial de R$5000,00 com uma taxa de juros fixa de 8% ao mês, depois de 10 meses, o valor do investimento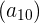 
é calculado usando a fórmula da progressão geométrica:
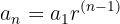
onde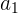 
é o investimento inicial, 
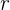é a razão de crescimento (1 + taxa de juros), e 
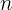é o número de meses. Então,
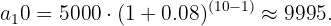
Um empréstimo de R$10000,00 para devolver em 12 meses com uma taxa de juros de 5% ao mês é amortizado mensalmente por meio de uma progressão geométrica. Quanto terá sido pago ao final dos 12 meses somente em juros?
A parcela mensal de amortização de um empréstimo de R$10000,00 para devolver em 12 meses com uma taxa de juros de 5% ao mês pode ser calculada utilizando a fórmula da progressão geométrica:
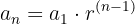
onde é o valor do empréstimo, 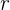é a razão de crescimento (1 + taxa de juros), e 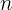é o número de meses. Então, terminamos pagando um total de:
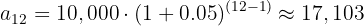
Ou seja, terá sido pago um total de R$17103 - R$10000 = R$7103 de juros.
O valor de um ativo diminui em 15% ao mês. Se o valor inicial é de r$50000, quanto valerá o ativo depois de 6 meses em uma progressão geométrica de depreciação?
Se o valor de um ativo diminui em 15% ao mês, depois de 6 meses, o valor do ativo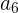 
é calculado utilizando a fórmula de progressão geométrica:
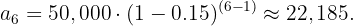
Suponha que seja feito um investimento de r$10000 com uma taxa de juros fixa de 5% ao ano. Quantos anos deve-se esperar para que o investimento seja dobrado?
Queremos encontrar a quantidade de anos que leva para o investimento chegar a 20,000€. Lembramos que a progressão geométrica é dada por 
. Então, buscamos um 
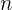tal que:
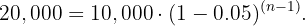
Resolvemos para :
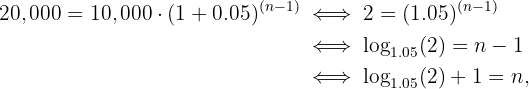
onde 
, ou seja, precisamos de 16 anos para dobrar o investimento.
Resumir com IA:
Gostou desse artigo? Deixe uma nota!
Loading...
