Bem-vindo e bem-vinda à nossa página dedicada a problemas de áreas e volumes! Aqui você encontrará uma coleção de desafiantes problemas de matemática relacionados à medição de áreas e volumes.
Antes de mais nada, precisamos entender que a área é uma medida que descreve a extensão de uma superfície bidimensional. Ela representa a quantidade de espaço ocupado por uma figura em um plano e é expressa em unidades quadradas, como metros quadrados (m²) ou centímetros quadrados (cm²).
Por outro lado, o volume é uma medida que descreve a quantidade de espaço tridimensional ocupado por um objeto. Ele representa o espaço encerrado dentro de uma figura ou sólido e é expresso em unidades cúbicas, como metros cúbicos (m³) ou centímetros cúbicos (cm³). Claro, tanto a área quanto o volume variam conforme o objeto.
Essas quantidades são fundamentais em muitas disciplinas, desde a arquitetura e a engenharia até a física e a geometria. Aqui, forneceremos explicações claras e passo a passo sobre como calcular a área e o volume de diferentes formas e sólidos, que podem aparecer tanto em problemas matemáticos quanto em situações do cotidiano.
Bora? Prepare-se para desenvolver suas habilidades na resolução de problemas. Aproveite e aprenda com as técnicas que preparamos especialmente para você.
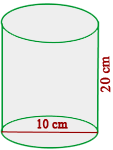
Calcule o volume, em centímetros cúbicos (cm³), de um cômodo que tem 5 metros de comprimento, 4 metros de largura e 2,5 metros de altura. Para calcular o volume de um retângulo, usamos a fórmula: V = comprimento × largura × altura Substituindo os valores dados: V=5 m × 4 m × 2,5 m =50 m³ Agora, para converter para centímetros cúbicos, lembre-se que 1 m = 100 cm. Portanto: V = 50 m³ = 50 × 100³ cm³ = 50 × 1.000.000 cm³ = 50.000.000 cm³ Logo, o volume da sala é 50.000.000 centímetros cúbicos. Uma piscina tem 8m de comprimento, 6m de largura e 1,5m de profundidade. O custo da pintura é de R$6 por metro quadrado. A) Quanto custará pintá-la? B) Quantos litros de água serão necessários para enchê-la? A) Quanto custará pintá-la? Primeiro, calculamos a área que será pintada. Como a piscina tem paredes e fundo, somamos as áreas dessas superfícies. Área das paredes laterais: 2 × (8 × 1,5) = 24 m² Agora, somamos as áreas: 24 + 18 + 48 = 90 m² O custo para pintar a piscina é R$6 por metro quadrado: 90 x 6 = 540 O custo para pintar a piscina é de R$540. B) Quantos litros de água serão necessários para enchê-la? Para calcular o volume da piscina, multiplicamos as três dimensões: comprimento, largura e profundidade. 8 × 6 × 1,5 = 72 m³ Sabemos que 1 metro cúbico (m³) equivale a 1.000 litros. Então, o volume em litros será: 72 × 1000 = 72.000 Serão necessários 72.000 litros de água para encher a piscina. Em um galpão de dimensões 5m de comprimento, 3m de largura e 2m de altura, queremos armazenar caixas com dimensões 10dm de comprimento, 6dm de largura e 4dm de altura. Quantas caixas poderemos armazenar? 1) Observamos que: 3) Calculamos o volume das caixas: A quantidade de caixas é obtida dividindo o volume do galpão pelo volume de uma caixa. Poderão ser armazenadas 125 caixas. Determine a área total de um tetraedro, um octaedro e um icosaedro com 5cm de aresta. 1) A área total de um tetraedro é: 2) A área total de um octaedro é: 3) A área total de um icosaedro é: Calcule a altura de um prisma que tem uma área de base de 12 dm² e uma capacidade de 48 L. Sabemos que a capacidade de um prisma é dada pela fórmula: Capacidade = Area da base × Altura - A capacidade fornecida é 48 L, o que equivale a 48 dm³ (pois 1 L = 1 dm³). Então, temos: 48 = 12 × Altura Agora, resolvemos para a altura: Logo, a altura do prisma é 4dm. Vamos calcular a quantidade de folha de alumínio necessária para fabricar 10 latas cilíndricas com 10 cm de diâmetro e 20 cm de altura. 1) Para calcular a quantidade de folha necessária para fabricar 10 latas cilíndricas: Fórmula para a área total de uma lata cilíndrica é: A = 2 πr 2 + 2 πrh 2) A quantidade gasta para fazer as 10 latas foi de: Portanto, serão necessários aproximadamente 7854 cm² de folhas de alumínio para as 10 latas. Um cilindro possui altura igual ao comprimento da circunferência da base. A altura mede cm. Calcule: a) A área total. Primeiro, é necessário fazer o cálculo do raio: a) Calculamos a área total. b) Calculamos o volume. Em uma proveta com raio de 6cm, são colocados quatro cubos de gelo com aresta de 4cm. A que altura chegará a água ao derreter? a) Calculamos o volume dos cubos de gelo: b) A proveta é cilíndrica, então seu volume é calculado: c) Igualamos os volumes e encontramos a altura: A cúpula de uma catedral tem formato semiesférico e raio de 50m. Se restaurá-la custa R$300 por m², qual será o orçamento total? a) Calculamos a área da semiesfera: b) Determinamos o custo da restauração: O custo será de R$ 4.712.400 Quantas azulejos de 30cmx30cm são necessários para revestir uma piscina com 10m de comprimento, 6m de largura e 3m de profundidade? a) Calculamos a área total a ser revestida: c) Dividimos para encontrar o número de azulejos necessários: Serão necessários 3900 azulejos. Um recipiente cilíndrico com raio de 10cm e altura de 5cm está cheio de água. Se o peso do recipiente cheio é de 2kg, qual é o peso do recipiente vazio? a) Calculamos o volume do cilindro: b) Subtraímos o peso da água do peso total para obter o peso do recipiente vazio: O recipiente pesa 0,492 kg Para uma festa, Luís fez 10 chapéus cônicos de papelão. Quanto papelão ele usou se cada chapéu tem 15cm de raio e 25cm de geratriz? a) Calculamos a área de um cone: Ele usou 11.781 cm² Um cubo com aresta de 20cm está cheio de água. Essa água caberia em uma esfera com raio de 20cm? a) Calculamos o volume do cubo: Calcule a diagonal de um paralelepípedo de 10 cm de comprimento, 4cm de largura e 5cm de altura. Utilizamos a fórmula da diagonal de um paralelepípedo: A diagonal tem 11,87cm Uma esfera e um cubo estão sendo preenchidos com água simultaneamente a uma taxa de 1m³ por minuto. Se a esfera tem raio de 5m e o cubo tem aresta de 8m, qual será preenchido primeiro? Calculamos o volume de cada recipiente. A fórmula para o volume da esfera é: O raio informado foi r = 5, então: A fórmula de volume do cubo com aresta a é: Dessa forma, se a = 8, o volume do cubo é: Como ambos recipientes são preenchidos à mesma taxa de 1m³ por minuto, a esfera será preenchida em aproximadamente 524 minutos, ou 2 horas e 44 minutos. Da mesma forma, o cubo será preenchido em 512 minutos, ou 2 horas e 32 minutos. Portanto, o cubo será preenchido com água primeiro.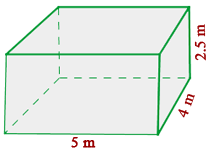
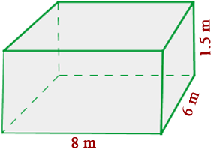
Área das outras duas paredes: 2 × (6 × 1,5) = 18 m²
Área do fundo da piscina: 8 × 6 = 48 m²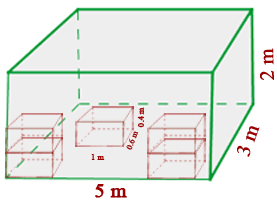
![]()
2) Calculamos o volume do galpão:![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
b) O volume.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
b) Calculamos a área de uma lajota:![]()
![]()
![]()
![]()
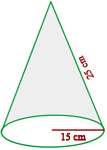
![]()
b) Multiplicamos pelo número de cones necessários:![]()
![]()
b) Calculamos o volume da esfera:![]()
Comparamos os volumes, e como o volume da esfera é maior que do cubo, concluímos que a água cabe na esfera.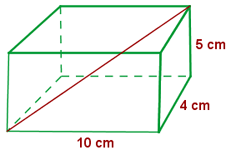
![]()
![]()
![]()
![]()
![]()
Resumir com IA:



