Temas

Operações variadas com números inteiros
Coloque, em ordem crescente, decrescente e represente graficamente os seguintes números inteiros:
1 -4, -1, 3, 2
2 -4, -1, 0, -7
3 2, 1, -1, 5 -3
4 −4, 6, −2, 1, −5, 0, 9
5 8, −6, −5, 3, − 2, 4, −4, 0, 7
1 -4, -1, 3, 2
Sentido crescente: − 4 < − 1 < 2 < 3
Sentido decrescente: 3 > 2 > -1 > -4
Representação gráfica:

2 -4, -1, 0, -7
Sentido crescente: − 7 < − 4 < -1 < 0
Sentido decrescente: 0 > -1 > -4 > -7
Representação gráfica:

3 2, 1, -1, 5, -3
Sentido crescente: − 3 < − 1 < 1 < 2 < 5
Sentido decrescente: 5 > 2 > 1 > -1 > -3
Representação gráfica:

4 −4, 6, −2, 1, −5, 0, 9
Sentido crescente: − 5 < − 4 < − 2 < 0 < 1 < 6 < 9
Sentido decrescente: 9 > 6 > 1 > 0 > -2 > -4 > -5
Representação gráfica:

5 8, −6, −5, 3, − 2, 4, −4, 0, 7
Sentido crescente: − 6 < − 5 < − 4 < − 2 < 0 < 3 < 4 < 7 < 8
Sentido decrescente: 8 > 7 > 4 > 3 > 0 > -2 > -4 > -5 > -6
Representação gráfica:

Valor absoluto e valor simétrico
Calcule os simétricos e os valores absolutos dos seguintes números inteiros:
1 -4, -1, 3, 2
2 -4, -1, 0, -7
3 2, 1, -1, 5 -3
4 −4, 6, −2, 1, −5, 0, 9
5 8, −6, −5, 3, − 2, 4, −4, 0, 7
1 -4, -1, 3, 2
Calculamos os simétricos:
-4 → -(-4)=4
-1 → -(-1)=1
3 → -(3)=-3
2 → -(2)=-2
Calculamos os valores absolutos:
|-4|=4
|-1|=1
|3|=3
|2|=2
2 -4, -1, 0, -7
Calculamos os simétricos:
-4 → -(-4)=4
-1 → -(-1)=1
0 → -(0)=0
-7 → -(-7)=7
Calculamos os valores absolutos:
|-4|=4
|-1|=1
|0|=0
|-7|=7
3 2, 1, -1, 5, -3
Calculamos os simétricos:
2 → -(2)=-2
1 → -(1)=-1
-1 → -(-1)=1
5 → -(5)=-5
-3 → -(-3)=3
Calculamos os valores absolutos:
|2|=2
|1|=1
|-1|=1
|5|=5
|-3|=3
4 −4, 6, −2, 1, −5, 0, 9
Calculamos os simétricos:
-4 → -(-4)=4
6 → -(6)=-6
-2 → -(-2)=2
1 → -(1)=-1
-5 → -(-5)=5
0 → -(0)=0
9 → -(9)=-9
Calculamos os valores absolutos:
|-4|=4
|6|=6
|-2|=2
|1|=1
|-5|=5
|0|=0
|9|=9
5 8, −6, −5, 3, − 2, 4, −4, 0, 7
Calculamos os simétricos:
8 → -(8)=-8
-6 → -(-6)=6
-5 → -(-5)=5
3 → -(3)=-3
-2 → -(-2)=2
4 → -(4)=-4
-4 → -(-4)=4
0 → -(0)=0
7 → -(7)=-7
Calculamos os valores absolutos:
|8|=8
|-6|=6
|-5|=5
|3|=3
|-2|=2
|4|=4
|-4|=4
|0|=0
|7|=7
Fatoração
Coloque em evidência o fator comum nas expressões:
1 3 · 2 + 3 · (−5) =
2 (−2) · 12 + (−2) · (−6) =
3 8 · 5 + 8 =
4 3 · 2 + 2 =
5 (−3) · (−2) + (−3) · (−5) =
Para este exercício, faremos uso da propriedade distributiva: a(b+c)= a·b + a·c
1 Solução direta: 3 · 2 + 3 · (−5) = 6 + (-15)= 6 - 15 = - 9
Fatoração: Podemos observar que o fator comum é o 3; colocamos em evidência usando a propriedade distributiva:
3( 2 + (-5) )
Verificação:
3(2+(-5)) = 3(2-5)=3(-3)= -9
2 (−2) · 12 + (−2) · (−6) = - 24 + 12 = -12
Fatoração: Podemos observar que o fator comum é o -2; colocamos em evidência usando a propriedade distributiva:
-2( 12 + (-6) )
Verificação:
-2( 12 + (-6) ) = -2( 12-6)= -2(6)=-12
3 8 · 5 + 8 = 40 + 8 = 48
Fatoração: Podemos observar que o fator comum é o 8; colocamos em evidência usando a propriedade distributiva:
8( 5+1 )
Verificação:
8( 5+1 ) =8(6)=48
4 3 · 2 + 2 = 6+ 2 = 8
Fatoração:Podemos observar que o fator comum é o 3; colocamos em evidência usando a propriedade distributiva:
2( 3+1 )
Verificação:
2( 3+1 ) =2(4)=8
5 (−3) · (−2) + (−3) · (−5) = 6 + 15 = 21
Fatoração: Podemos observar que el factor común es el -3, lo extraemos usando la propiedad distributiva
-3( (-2)+(-5) )
Verificação:
-3( (-2)+(-5) ) = -3(-2-5)= -3(-7)=21
Operações básicas com números inteiros
Faça as seguintes operações com números inteiros:
1 2 − (-3) -(-1)
2 -4 − 3 -(-5)
3 (3 − 8) + [5 − (−2)]
4 5 − [6 − 2 − (1 − 8) −3 + 6] + 5
5 [12 : 2] : 3
6 9 : [6 : (− 2)]
7 [24 : (-3)]: [16 : (− 4)]
8 [(−2)5 − (−3)³]²
9 (5 + 3 · 2 : 6 − 4 ) · (4 : 2 − 3 + 6) : (7 − 8 : 2 − 2)²
10 [(17 − 15)³ + (7 − 12)²] : [(6 − 7) · (12 − 23)]
1 2 − (-3) -(-1) =
Escrevemos o simétrico de (−3) e (-1)
= 2 + 3+1 =
Realizamos a soma:
= 2+3+1 = 6
2 -4 − 3 -(-5) =
Escrevemos o simétrico de (−5)
= -4 - 3+5 =
Fazemos a adição e subtração:
= -4-3+5 = -2
3 (3 − 8) + [5 − (−2)] =
Escrevemos o simétrico de (−2)
= −5 + (5 + 2) =
Operamos o que está entre parênteses:
= −5 + 7 = 2
4 5 − [6 − 2 − (1 − 8) − 3 + 6] + 5 =
Operamos o que está entre parênteses:
= 5 − [6 − 2 − (−7) − 3 + 6] + 5 =
Calculamos o simétrico de (−7)
= 5 − (6 − 2 + 7 − 3 + 6) + 5 =
Operamos dentro dos parentesis e usamos o simétrico do resultado:
= 5 − 14 + 5 = −4
5 [12 : 2] : 3 =
Realizamos a divisão entre colchetes:
= [12 : 2]:3 = 6:3
Realizamos a divisão entre colchetes:
= 6:3=2
6 9 : [6 : (−2)] =
Realizamos a divisão entre colchetes:
= 9 : [6 : (−2)]=9 : (−3)
Realizamos a divisão restante:
= 9 : (−3)=-3
7 [24 : (-3)]: [16 : (− 4)] =
Realizamos a divisão entre colchetes:
= [24 : (-3)]: [16 : (− 4)]=-8 : (−4)
Realizamos a divisão restante:
= -8 : (−4)=2
8 [(−2)5 − (−3)³]² =
Realizamos as potências dos parênteses. Para ((−2)5 calculamos da seguinte forma: (-2)(-2) = 4. 4(-2) = -8. -8 (-2) = 16. 16 (-2) = -32. Para (−3)³, seguindo o mesmo método de cálculo: (-3)(-3) = 9. 9 (-3) = -27
= [−32 − (−27)]² =
Removemos os parênteses:
= (−32 + 27)² =
Realizamos a operação e elevamos ao quadrado:
= (−5)² = 25
9 (5 + 3 · 2 : 6 − 4 ) · (4 : 2 − 3 + 6) : (7 − 8 : 2 − 2)² =
Realizamos 3 · 2 (primeiro fazemos a multiplicação) e as divisões:
= (5 + 6 : 6 − 4 ) · (2 − 3 + 6) : (7 − 4 − 2)² =
Efetuamos a divisão:
= (5 + 1 − 4 ) · (2 − 3 + 6) : (7 − 4 − 2)² =
Operamos cada parêntese:
= 2 · 5 : 1² =
Elevamos ao quadrado:
= 2 · 5 : 1 =
Primeiro multiplicamos e depois dividimos:
= 10 : 1 =10
10 [(17 − 15)³ + (7 − 12)²] : [(6 − 7) · (12 − 23)]
Operamos os parênteses:
= [(2)³ + (−5)²] : [(−1) · (−11)]
Calculamos as potências:
= (8 + 25) : [(−1) · (−11)] =
Operamos os parênteses e o colchete, e dividimos os resultados:
= 33 : 11 = 3
Ordem das operações
Realize as seguintes operações com números inteiros:
1 10:5+2
2 10+6:3
3 6 · 3+6:3
4 18:6- 4· 3
5(7 − 2 + 4) − (2 − 5)
6 1 − (5 − 3 + 2) − [5 − (6 − 3 + 1) − 2]
7 −12 · 3 + 18 : (−12 : 6 + 8)
82 · [( −12 + 36) : 6 + (8 − 5) : (−3)] - 6
9 [(−2)5 · (−3)2] : (−2)2 = (−32 · 9) : 4
10 6 + {4 − [(17 − (4 · 4)] + 3} − 5
1 10:5+2 =
Realizamos a divisão:
= 10:5+2 = 2+2
Fazemos a soma:
= 2+2 = 4
2 10+6:3 =
Realizamos a divisão:
= 10+6:3 = 10+2
Fazemos a soma:
= 10+2 = 12
3 6 · 3+6:3 =
Realizamos a multiplicação e a divisão:
= 6 · 3+6:3 = 18+2
Fazemos a soma:
= 18+2 = 20
4 18:6- 4· 3 =
Realizamos a multiplicação e a divisão:
= 18:6- 4· 3 = 3-12
Fazemos a subtração:
= 3-12 = -9
5 (7 − 2 + 4) − (2 − 5) =
Operamos os parênteses:
= 9 − (−3) =
Usamos o simétrico de (−3)
= + 3 = 12
6 1 − (5 − 3 + 2) − [5 − (6 − 3 + 1) − 2] =
Operamos os parênteses:
= 1 − (4) − [5 − (4) − 2] =
Aplicamos os simétricos dos 4
= 1 − 4 − (5 − 4 − 2) =
Operamos os parênteses:
= 1 − 4 − 5 + 4 + 2 =
Somamos:
= 1 − 5 + 2 = −2
7 −12 · 3 + 18 : (−12 : 6 + 8) =
Realizamos a divisão do parêntese:
= − 12 · 3 + 18 : (−2 + 8) =
Operamos os parênteses:
= −12 · 3 + 18 : 6 =
Realizamos a multiplicação e a divisão:
= −36 + 3 = −33
8
2 · [( −12 + 36) : 6 + (8 − 5) : (−3)] − 6 =
Realizamos as operações nos dois primeiros parênteses:
= 2 · [24 : 6 + 3 : (−3)] − 6 =
Efetuamos as divisões:
= 2 · [ 4 + (−1)] − 6 =
Operamos o colchete:
= 2 · 3 − 6 =
Efetuamos o produto:
= 6 − 6 = 0
9 [(−2)5 · (−3)²] : (−2)² =
Fazemos as potências:
= (−32 · 9) : 4 =
Operamos os parênteses:
= −288 : 4 = −72
10 6 + {4 − [(17 − (4 · 4)] + 3} − 5 =
Realizamos o produto:
= 6 + [4 − (17 − 16) + 3] − 5 =
Operamos o parêntese e aplicamos o simétrico:
= 6 + (4 − 1 + 3) − 5 =
Operamos os parênteses:
= 6 + 6 − 5 = 7
Soluções fora e dentro do conjunto dos números reais
Calcule o resultado da potência e então verifique se o resultado obtido possui raiz quadrada no conjunto dos números reais.
1 (−2)²
2 (−4)²
3 (−9)²
4 (−5)3
5 (−3)5
6 (−1)7
7 (−3)² · (−3)
8 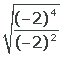
9 (−2)³
10 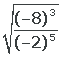
1(−2)² = 4
A raiz quadrada de 4 é ± 2
2(−4)² = 16
A raiz quadrada de 16 é ± 4
3(−9)² = 81
A raiz quadrada de 81 é ± 9
4(−5)3 = −125
A raiz quadrada de -125 não existe no conjunto dos números reais, portanto, essa raiz não tem solução nos reais.
Em geral, não existe raiz quadrada de número negativo nos reais, pois nenhum número elevado ao quadrado resulta em valor negativo.
5 (−3)5 = −243
A raiz quadrada de -243
não existe no conjunto dos números reais, portanto, essa raiz não tem solução nos reais.
Em geral, não existe raiz quadrada de número negativo nos reais, pois nenhum número elevado ao quadrado resulta em valor negativo.
6 (−1)7 = −1
A raiz quadrada de -1 não existe no conjunto dos números reais, portanto, essa raiz não tem solução nos reais.
Em geral, não existe raiz quadrada de número negativo nos reais, pois nenhum número elevado ao quadrado resulta em valor negativo.
7 (−3)² · (−3) =
Realizamos o produto das potências e elevamos ao cubo:
= (−3)³ = −27
A raiz quadrada de −27 não tem solução.
8 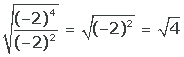
Realizamos a divisão de potências, elevamos ao quadrado e extraímos a raiz.
O resultado é 2, e existe raiz quadrada de 2 no conjunto dos números reais.
9 (−2)³ = −8
A raiz quadrada de -8 não tem solução no conjunto dos números reais.
10 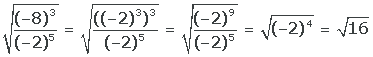
Colocamos 8 escrito como potência, aplicada uma potência de potência no numerador, depois divisão de potências, elevamos à quarta potência e extraímos a raiz
O resultado é 4, e a raiz quadrada de 4 é ±2.
Operações com potências
Calcule as seguintes operações com potências de números inteiros:
1 (−2)² · (−2)³ · (−2)4
2 (−8) · (−2)² · (−2)0 (−2)
3(−2)−2 · (−2)³ · (−2)4
4 2−2 · 2−3 · 24
5 2² : 2³
6 2-2 : 2³
7 2² : 2-3
8 2-2 : 2-3
9 [(−2)− 2] 3 · (−2)³ · (−2)4
10[(−2)6 : (−2)³]³ · (−2) · (−2)−4
Para resolver estes exercícios, utilizaremos as leis dos expoentes:
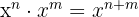
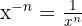

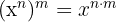
1 (−2)² · (−2)³ · (−2)4 = (−2)9 = −512
O resultado será negativo porque a base é negativa e o expoente é ímpar.
2 (−8) · (−2)² · (−2)0 (−2) =
Primeiro decompomos o 8 em fatores:
(−2)³ · (−2)² · (−2)0 · (−2) = (−2)6 = 64
O resultado será positivo porque a base é negativa e o expoente é par.
3 (−2)−2 · (−2)³ · (−2)4 = (−2)5 = −32
4 2−2 · 2−3 · 24 = 2−1 = 1/2
Como o expoente é negativo, tomamos o inverso da base, aplicando a regra dos expoentes negativos.
5 2² : 2³ = 2−1 = 1/2
Como o expoente é negativo, devemos tomar o inverso da base, ou seja, aplicar a respectiva lei dos expoentes.
6 2−2 : 2³ = 2−5 = 1/25 = 1/32
7 2² : 2−3 = 25 = 32
8 2−2 : 2−3 = 2
9 [(−2)−2]³ · (−2)³ · (−2)4 = (−2)−6 · (−2)7 = −2
10 [(−2)6 : (−2)³] 3 · (−2)· (−2)−4 = [(−2)³]³ · (−2)−3 = (−2)9 · (−2)−3= (−2)6 = 64
Uso de expoentes em operações com números inteiros
Faça as seguintes operações com potências de números inteiros:
1 (−3)1 · (−3)³ · (−3)4 =
2(−27) · (−3) · (−3)² · (−3)0=
3 (−3)² · (−3)³ · (−3)−4 =
4 3−2 · 3−4 · 34 =
5 5² : 5³ =
6 5-2 : 5³ =
7 5² : 5-3 =
8 5-2 : 5-3 =
9 (−3)1 · [(−3)³]² · (−3)−4 =
10 [(−3)6 : (−3)³]³ · (−3)0 · (−3)−4 =
1 (−3)1 · (−3)³ · (−3)4 = (−3)8 = 6561
2 (−27) · (−3) · (−3)² · (−3)0= (−3)³ · (−3) · (−3)² · (−3)0 = (−3)6 = 729
3 (−3)² · (−3)³ · (−3)−4 = −3
4 3−2 · 3−4 · 34 = 3−2 = 1/3² = 1/9
5 5² : 5³ = 5−1 = 1/5
6 5−2 : 5³ = 5−5 = 1/55 = 1/3125
7 5² : 5−3 = 55 = 3125
8 5−2 : 5−3 = 5
9 (−3)1 · [(−3)³]² · (−3)−4 = (−3)1 · (−3)6· (−3)−4 = (−3)³
Primeiro, calculamos a potência de uma potência e, depois, multiplicamos.
10 [(−3)6 : (−3)³]³ · (−3)0 · (−3)−4 = [(−3)³]³ · (−3)0· (−3)−4 = (−3)9 · (−3)0 · (−3)−4 = (−3)5 =−243
Em primeiro lugar, fazemos a divisão indicada entre colchetes, depois calculamos a potência de uma potência e, por fim, multiplicamos as potências.
Resumir com IA:












