Temas
Para poder resolver estes exercícios devemos lembrar que a definição de logaritmo é de que, se  é igual ao logaritmo, base
é igual ao logaritmo, base  , de
, de 

isto implica que  . Com isto em mente, passamos ao exercício.
. Com isto em mente, passamos ao exercício.

Calcule o valor de y aplicando a definição de logaritmo.
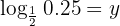
Nossa expressão é:

Aplicamos a definição de logaritmo e passamos  para fração, isto é
para fração, isto é  , depois simplificamos
, depois simplificamos
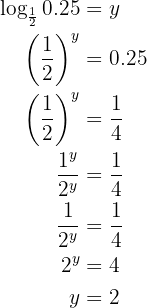
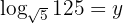
Nossa expressão é:
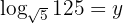
Aplicamos a definição de logaritmo:
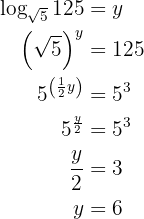
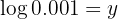
Nossa expressão é:
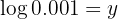
Note que ao escrevermos 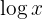 nos referimos à base
nos referimos à base  , isto é
, isto é 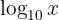 . Aplicamos a definição de logaritmo:
. Aplicamos a definição de logaritmo:
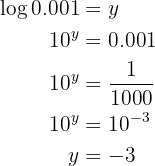
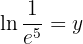
Nossa expressão é:
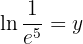
Lembre-se que o logaritmo natural é simplesmente o logaritmo base  , isto é,
, isto é, 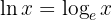 . Aplicamos a definição de logaritmo e resolvemos:
. Aplicamos a definição de logaritmo e resolvemos:
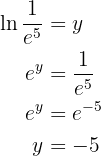
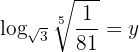
Nossa expressão é:
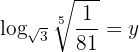
Aplicamos a definição de logaritmo e resolvemos:
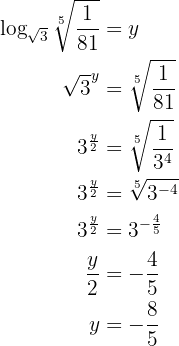
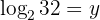
Nossa expressão é:
3 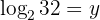
Aplicamos a definição de logaritmo e resolvemos:
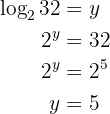
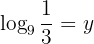
Nossa expressão é:
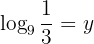
Aplicamos a definição de logaritmo e resolvemos:
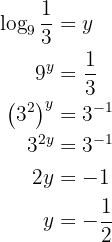

Nossa expressão é:

Aplicamos a definição de logaritmo e resolvemos:
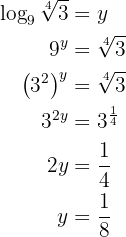

Nossa expressão é

Aplicamos a definição de logaritmo e resolvemos. Note que neste caso é um pouco diferente já que o  é a base do logaritmo.
é a base do logaritmo.
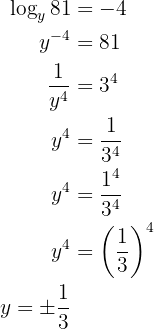
Nossa expressão é:

Aplicamos a definição de logaritmo e resolvemos. Note que neste caso é um pouco diferente já que o  é a base do logaritmo.
é a base do logaritmo.
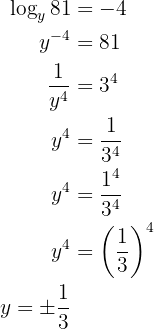
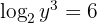
Nossa expressão é:
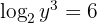
Aplicamos a definição de logaritmo e resolvemos. Note que neste caso é um pouco diferente já que  encontra-se no argumento do logaritmo
encontra-se no argumento do logaritmo
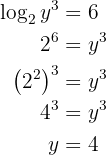
Calcule os seguintes logaritmos
Sendo 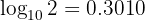 , calcule o seguinte logaritmo
, calcule o seguinte logaritmo
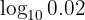
Nossa expressão é
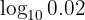
Procedemos convertendo o argumento em uma fração adequada
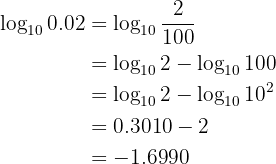
Sendo 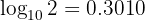 , calcule o seguinte logaritmo
, calcule o seguinte logaritmo


Procedemos escrevendo 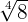 como uma potência de
como uma potência de  .
.
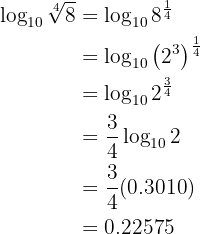
Sendo 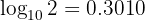 , calcule o seguinte logaritmo
, calcule o seguinte logaritmo
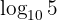
Nossa expressão é:
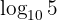
Procedemos escrevendo  como
como  e posteriormente aplicamos algumas propriedades dos logaritmos
e posteriormente aplicamos algumas propriedades dos logaritmos
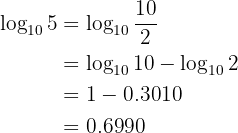
Sendo 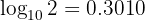 , calcule o seguinte logaritmo
, calcule o seguinte logaritmo
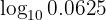
Nossa expressão é
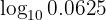
Procedemos escrevendo 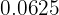 como uma fração na qual haja uma potência de
como uma fração na qual haja uma potência de  e aplicamos propriedades dos logaritmos
e aplicamos propriedades dos logaritmos
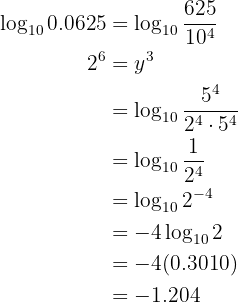
Desenvolva o cálculo das seguintes expressões
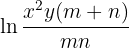
Nossa expressão é:
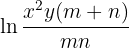
Vamos para exercício:
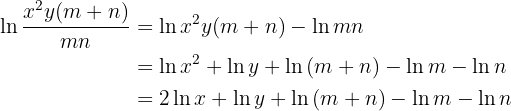

Nossa expressão é:

Vamos para o exercício
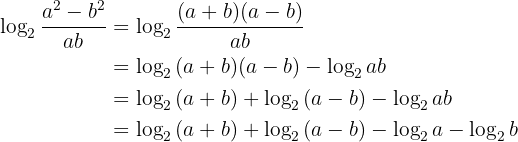
Descubra o valor de  utilizando logaritmos
utilizando logaritmos
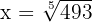
Nossa expressão é:
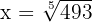
Vamos para o exercício:
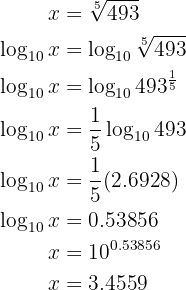

Nossa expressão é:

Veja o exercício:
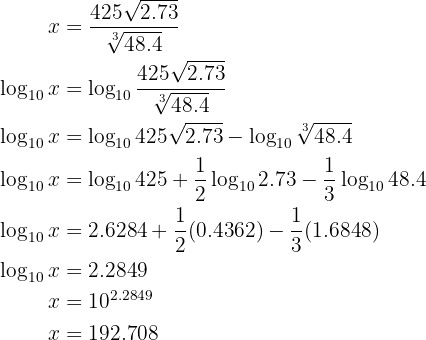

Nossa expressão é a

Começando o exercício:

Resumir com IA:












