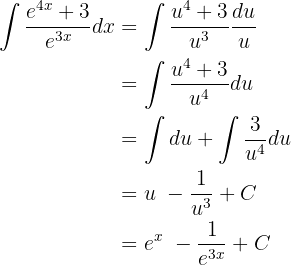Temas

O que é uma integral e para que serve?
A integral é principalmente conhecida como a operação inversa da derivada, e sua principal função é calcular a área sob uma curva. Ela está intimamente relacionada ao estudo do cálculo infinitesimal.
Dado curioso:
Você já percebeu que, ao resolver uma integral, sempre adicionamos uma constante?
Por exemplo:
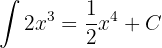
Se pensarmos um pouco, isso faz muito sentido, pois a derivada de qualquer constante é  , o que significa que ao derivar uma constante, ela desaparece. O lógico é que, ao aplicar a operação contrária à derivada, ou seja, ao integrar o valor
, o que significa que ao derivar uma constante, ela desaparece. O lógico é que, ao aplicar a operação contrária à derivada, ou seja, ao integrar o valor  , o resultado será uma constante.
, o resultado será uma constante.
Sobre os métodos para resolver integrais
Assim como nas derivadas, as integrais possuem dois métodos principais:
1 Através do conceito de limite
2 Através de fórmulas para casos específicos
Pode-se dizer que, para cada forma de resolver uma derivada, existe uma forma de resolver uma integral.
Exemplo:
Dada a função 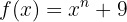
Sua derivada é 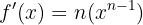 e a integral dela seria
e a integral dela seria 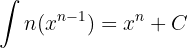
Exercícios propostos sobre integração
Integre as seguintes funções:
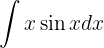
Integraremos esta função "por partes".
Lembramos que isso nos diz que:

Agora, decidimos qual parte da função será  e qual será
e qual será  . Neste caso, faremos da seguinte maneira:
. Neste caso, faremos da seguinte maneira:

e
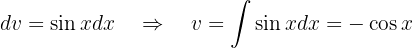
Substituindo esses valores na fórmula de integração por partes, temos:
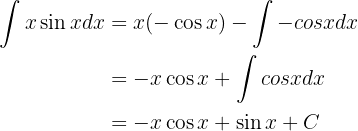
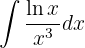
Integraremos esta função "por partes".
Lembramos que isso nos diz que:

Agora, decidimos qual parte da função será  e qual será
e qual será  . Neste caso, faremos da seguinte maneira:
. Neste caso, faremos da seguinte maneira:
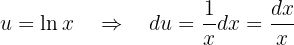
e
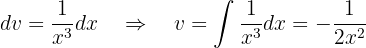
Substituindo esses valores na fórmula de integração por partes, temos:
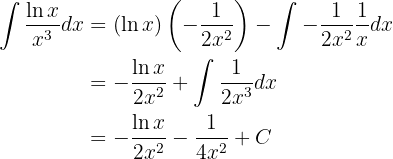
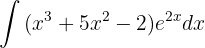
Integraremos esta função "por partes".
Lembramos que isso nos diz que:

Agora, decidimos qual parte da função será  e qual será
e qual será  . Neste caso, faremos da seguinte maneira:
. Neste caso, faremos da seguinte maneira:
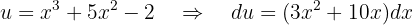
e

Substituindo esses valores na fórmula de integração por partes, temos:
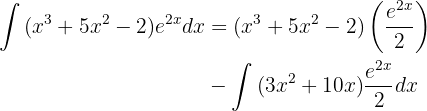
Vamos aplicar novamente a integração por partes para integrar:

Neste caso  e
e  serão:
serão:

e
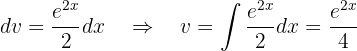
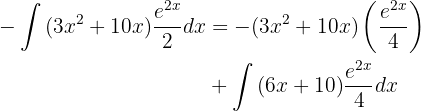
Por fim, aplicaremos novamente a integração por partes para integrar:

neste caso  e
e  serán
serán
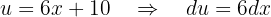
e
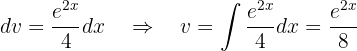
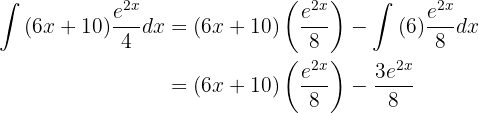
Substituindo tudo isso na primeira integral, temos:
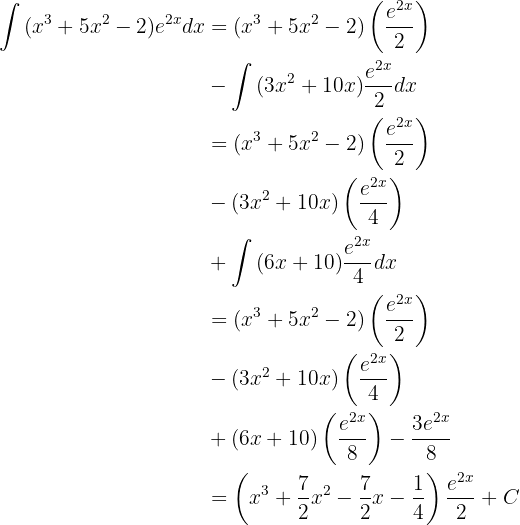
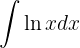
Integraremos esta função "por partes".
Lembramos que isso nos diz que:

Agora, decidimos qual parte da função será  e qual será
e qual será  . Neste caso, faremos da seguinte maneira:
. Neste caso, faremos da seguinte maneira:
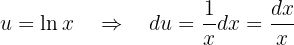
e
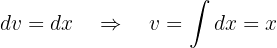
Substituindo esses valores na fórmula de integração por partes, temos que:
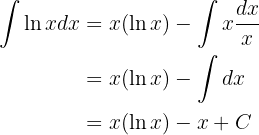
Integraremos esta função "por partes".
Lembramos que isso nos diz que:

Agora, decidimos qual parte da função será  e qual será
e qual será  . Neste caso, faremos da seguinte maneira:
. Neste caso, faremos da seguinte maneira:
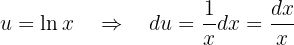
e
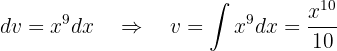
Substituindo esses valores na fórmula de integração por partes, temos que:
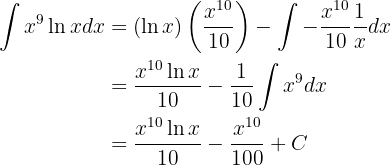
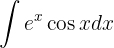
Integraremos esta função "por partes".
Lembramos que isso nos diz que:

Agora, decidimos qual parte da função será  e qual será
e qual será  . Neste caso, faremos da seguinte maneira:
. Neste caso, faremos da seguinte maneira:

e
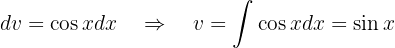
Substituindo esses valores na fórmula de integração por partes, temos que:
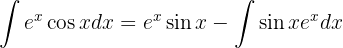
Voltamos a aplicar integração por parte para integrar:
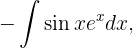
Neste caso,  e
e  serão:
serão:

e
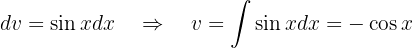
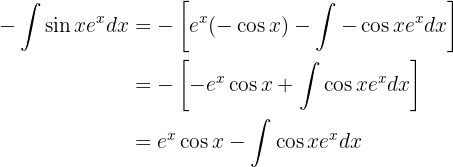
Substituindo tudo isso na nossa primeira integral, vemos que a integral que desejamos calcular aparece tanto no lado esquerdo quanto no lado direito, mas com sinal negativo. Portanto, o que precisamos fazer é isolar a integral que queremos encontrar, somando-a de ambos os lados da equação.
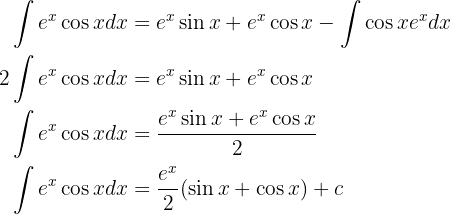
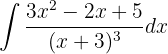
Para integrar esta função, primeiro precisamos simplificar a função:

Para simplificá-la e deixá-la em uma expressão fácil de integrar, aplicaremos frações parciais. Não explicaremos a fundo a teoria de frações parciais, mas tentaremos escrever cada passo para evitar qualquer confusão.
Dado que o denominador é um polinômio de ordem 1 elevado à terceira potência, temos que, em geral, nossa expressão pode ser escrita como:
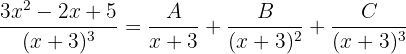
para determinados números reais  ,
,  e
e  .
.
Para encontrar os valores dessas incógnitas, devemos realizar as somas e depois igualar os coeficientes dos termos de mesmo grau, ou seja,
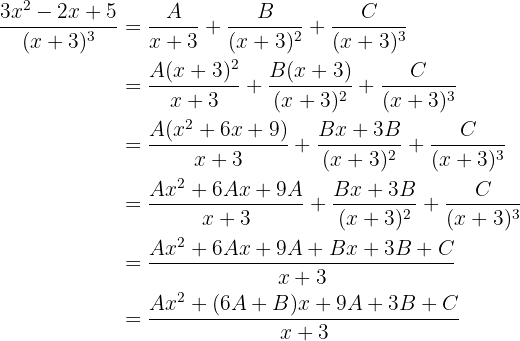
Isso nos leva a:
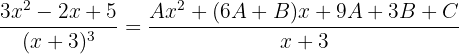
Portanto, os numeradores são iguais:
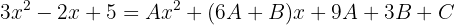
E os coeficientes dos termos de mesmo grau também são iguais. Ou seja:

Da primeira igualdade, é direto que 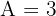 . Substituindo o valor de
. Substituindo o valor de  na segunda igualdade, temos:
na segunda igualdade, temos:
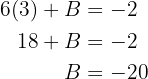
Substituindo os valores de 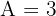 e
e  na terceira igualdade, temos que:
na terceira igualdade, temos que:
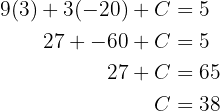
Assim, temos que nossa função é igual a:

Agora, procedemos para integrar. Usaremos o método de mudança de variável. Para isso, usaremos:

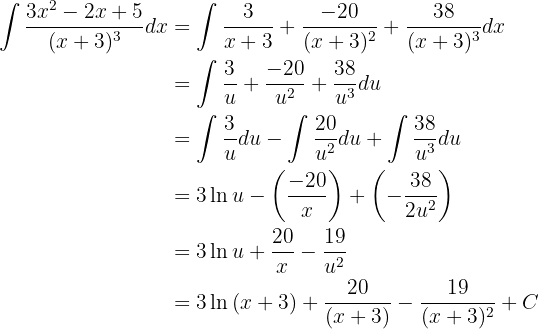

Vamos fazer a integração usando 0 método de mudança da variável. Assim:
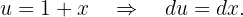
Note que, também,  . Assim, substituindo na integral original:
. Assim, substituindo na integral original:
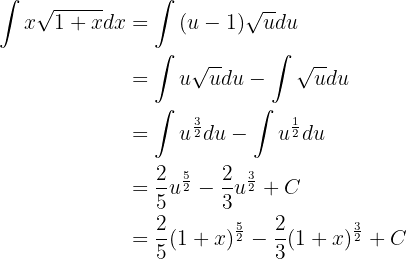
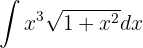
Novamente, vamos fazer a integração usando o método de mudança de variável. Usamos:
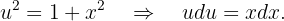
Também note que  . Assim, substituindo na integral original:
. Assim, substituindo na integral original:
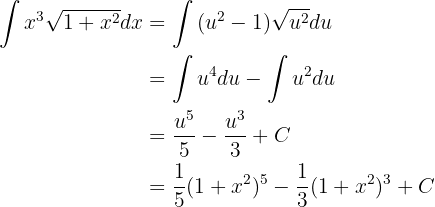
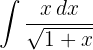
Novamente, vamos fazer a integração usando o método de mudança de variável. Usamos:
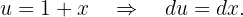
Também note que,  . Assim, substituindo na integral original:
. Assim, substituindo na integral original:
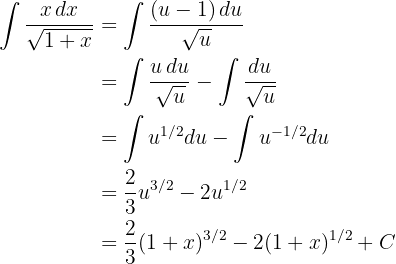
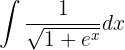
Novamente, vamos fazer a integração usando o método de mudança de variável. Assim:

Agora, vamos isolar os diferenciais:
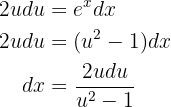
E substituímos na integral original:
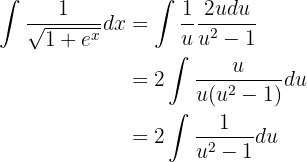
Aplicaremos frações parciais para simplificar essa fração e expressá-la como uma soma de frações fáceis de integrar. Temos que:
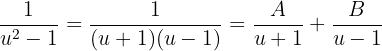
Desenvolvendo a última soma, temos:
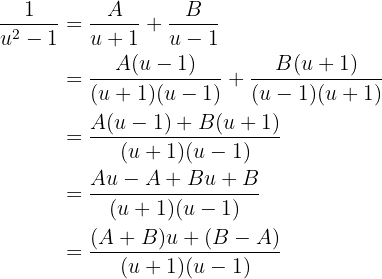
Igualando os numeradores, temos que: 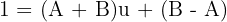 daí, obtemos que:
daí, obtemos que:

Note que da primeira igualdade obtemos que  , e da segunda,
, e da segunda, 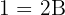 , logo,
, logo,

Portanto, temos que:
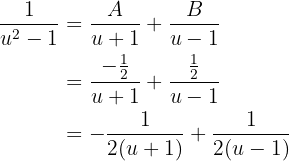
Fazendo a substituição na integral:

Agora, substituímos o valor de  nos termos de
nos termos de  , ou seja,
, ou seja, 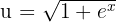
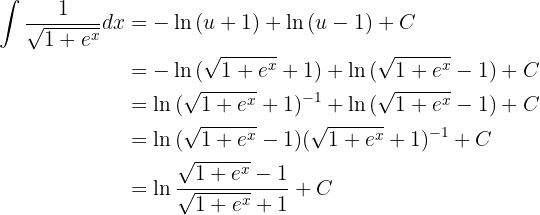
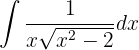
Vamos integrar por substituição trigonométrica. Dessa forma:
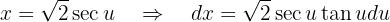
Substituindo esses valores na integral, temos:
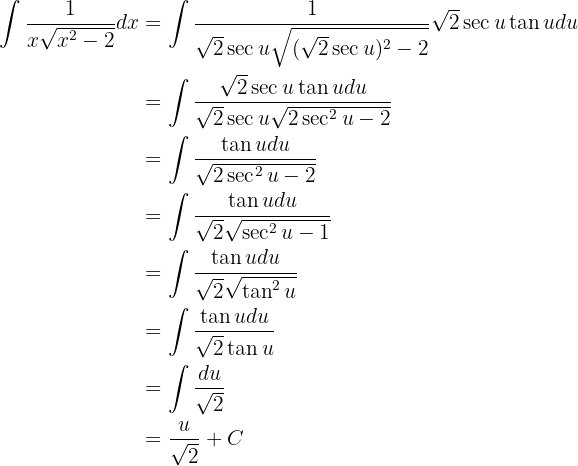
Por fim, para reescrever isso em termos de  , note que ao fazer a substituição de
, note que ao fazer a substituição de  , isolamos
, isolamos  a partir daqui:
a partir daqui:
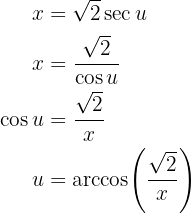
Substituindo, temos:
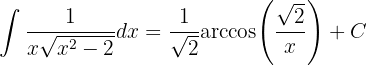
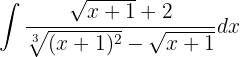
Vamos integrar esta função usando o método de mudança de variável.
Assim:
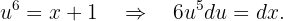
Substituindo os valores na integral, obtemos
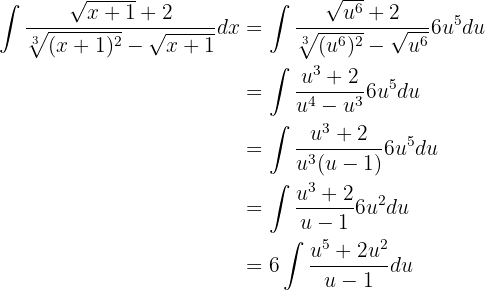
Vamos simplificar a expressão dentro da integral usando frações parciais. Desta maneira:
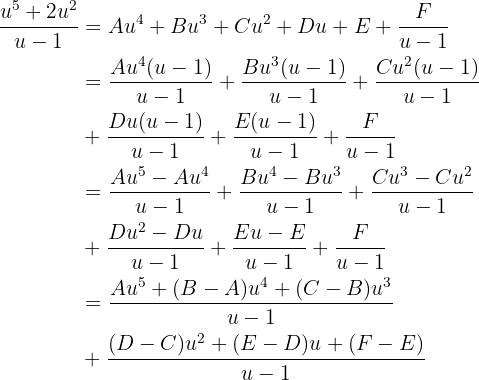
O que nos dá o seguinte sistema de equações:
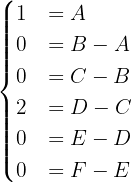
De onde temos 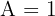 ,
,  ,
, 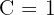 ,
,  ,
, 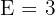 e
e 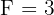 . Assim, a expressão fica dessa forma:
. Assim, a expressão fica dessa forma:
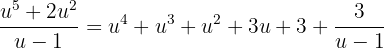
Fazendo a substituição na integral, temos:
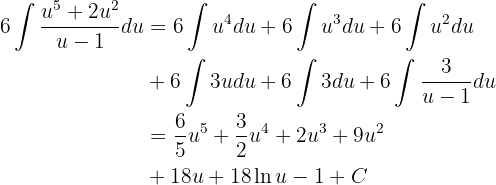
Por fim, vamos escrever em termos de  . Para isso, note que
. Para isso, note que 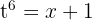 , portanto,
, portanto, 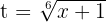 , Substituindo, obtemos:
, Substituindo, obtemos:
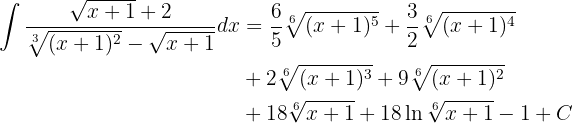
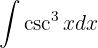
Vamos integrar usando o método de mudança de variável. Primeiro, note que:
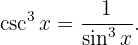
O método de mudança de variável será:
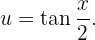
Derivando, podemos ver que:
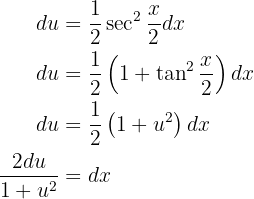
Considerando que na integral temos 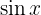 , devemos expressar essa função em termos de
, devemos expressar essa função em termos de 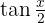 para poder substituir na integral em termos de
para poder substituir na integral em termos de  . Vamos lembrar da seguinte identidade trigonométrica:
. Vamos lembrar da seguinte identidade trigonométrica:
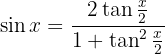
Ou seja, temos que:
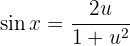
Substituindo na integral, obtemos:
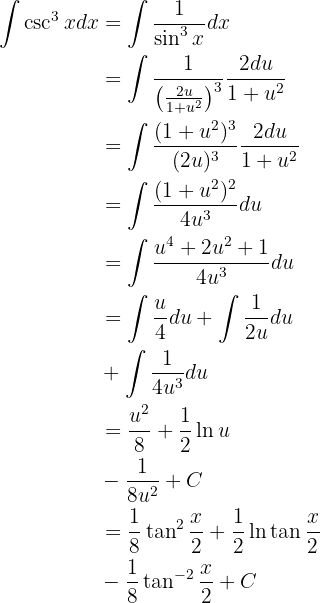
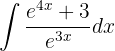
Vamos integrar usando o método de mudança de variável. Assim:
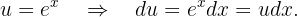
Do diferencial, obtemos que:  . Agora, fazendo a substituição na integral, obtemos:
. Agora, fazendo a substituição na integral, obtemos: