Para essa seleção de exercícios supomos que você já tenha algum conhecimento sobre a definição de inequação e algumas de suas propriedades. Caso contrário, você pode visitar nossa artigo sobre a teoria.
Resolveremos cada um dos exercícios passo a passo. Devemos notar que resolver uma inequação é praticamente igual à isolar em uma igualdade. Simplesmente devemos prestar muita atenção às propriedades das inequações quando estas “mudam de lado”, etc. Faremos cada passo algebraico tentando detalhar o máximo possível para você.
Encontre a solução de cada uma das seguintes inequações ou sistema de inequações e faça um gráfico do seu conjunto solução.
1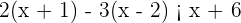
Procedemos a resolver a inequação. Lembre-se de que é muito parecido com isolar em uma igualdade, só que agora em vez de encontrar apenas um valor para nossa variável, vamos encontrar todo um domínio, muitas vezes formado por um intervalo ou por uniões e interseções de intervalos. Nossa inequação é:
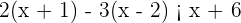
Para resolver a equação, primeiro usaremos as propriedades distributivas e depois vamos isolar o 
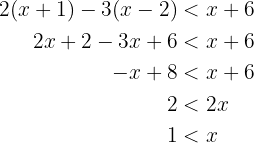
Note que  , assim, sabemos que seu conjunto de solução é o intervalo
, assim, sabemos que seu conjunto de solução é o intervalo  .
.

2
A inequação que deve ser resolvida é a seguinte:

Para resolver, primeiro nos desfazemos das frações e depois isolamos o  . Para nos desfazermos das frações precisamos do mínimo múltiplo comum dos denominadores, que é
. Para nos desfazermos das frações precisamos do mínimo múltiplo comum dos denominadores, que é  , assim, obteremos
, assim, obteremos

Note que  , assim, sabemos que seu conjunto de solução é o intervalo
, assim, sabemos que seu conjunto de solução é o intervalo  .
.

3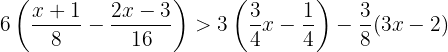
A inequação que deve ser resolvida é a seguinte:
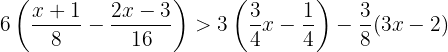
Para resolver devemos fazer igual que nos exercícios anteriores, ou seja, precisamos aplicar a lei distributiva e, além disso, eliminar as frações

Note que 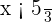 , assim, sabemos que seu conjunto de solução é o intervalo
, assim, sabemos que seu conjunto de solução é o intervalo  .
.
4 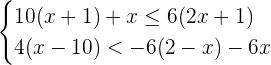
Para resolver este sistema devemos resolver as inequações separadamente e depois encontrar os valores para os quais  cumpra ambas inequações.
cumpra ambas inequações.
Começamos com a primeira inequação

a partir da primeira inequação sabemos que  , ou seja, que
, ou seja, que  pertence ao intervalo
pertence ao intervalo  . Agora resolvemos a segunda inequação
. Agora resolvemos a segunda inequação
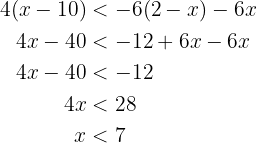
a partir da segunda inequação sabemos que 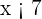 , ou seja, que
, ou seja, que  pertence ao intervalo
pertence ao intervalo  . Note que x deve cumprir ambas condições, isto é,
. Note que x deve cumprir ambas condições, isto é,  e
e 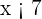 , Isso é equivalente a dizer que
, Isso é equivalente a dizer que  encontra-se na interseção dos intervalos
encontra-se na interseção dos intervalos  e
e  , assim, o conjunto de solução é
, assim, o conjunto de solução é


5 
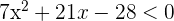
Começamos a resolver o exercício
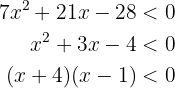
Note que isto quer dizer que 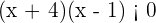 , no entanto, o produto é negativo apenas quando as expressões que são multiplicadas têm sinais contrários, isto é, temos dois casos principais. Um em que
, no entanto, o produto é negativo apenas quando as expressões que são multiplicadas têm sinais contrários, isto é, temos dois casos principais. Um em que 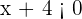 e
e  , e outro caso em que
, e outro caso em que  e
e 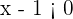 .
.
Avaliamos cada caso, começando pelo primeiro. Supomos que 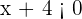 , então
, então 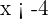 , além disso, sabemos que
, além disso, sabemos que  , então
, então  , isto é
, isto é  deve cumprir
deve cumprir 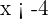 e
e  , ou seja, deve pertencer à interseção dos intervalos
, ou seja, deve pertencer à interseção dos intervalos  e
e  . Note que a interseção é vazia já que não há interseção nos intervalos, portanto, neste caso, não obteremos nenhuma solução.
. Note que a interseção é vazia já que não há interseção nos intervalos, portanto, neste caso, não obteremos nenhuma solução.
Agora passamos para o segundo caso. Suponhamos que  , então
, então  , além disso, sabemos que
, além disso, sabemos que 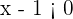 , então
, então 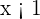 , isto quer dizer que
, isto quer dizer que  deve cumprir
deve cumprir  e
e 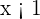 , ou seja, deve pertencer à interseção dos intervalos
, ou seja, deve pertencer à interseção dos intervalos  e
e  . Note que a interseção é
. Note que a interseção é  , este intervalo é a solução que procurávamos.
, este intervalo é a solução que procurávamos.

6 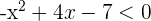
Resolvemos nossa inequação
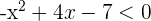
Começamos a resolver o exercício
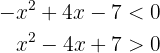
Note que para expressar  como produto de expressões do primeiro grau devemos encontrar suas raízes. Para isso, utilizando a fórmula quadrática sabemos que
como produto de expressões do primeiro grau devemos encontrar suas raízes. Para isso, utilizando a fórmula quadrática sabemos que

no entanto, note que temos a raiz quadrada de um número negativo, portanto as raízes do polinômio são ambos números complexos. Dito isso, como não podemos escrever o polinômio como um produto de expressões do primeiro grau com número real, para encontrar a solução vamos substituir  por um número real qualquer que podemos escolher. Se a equação se cumpre, saberemos então que a solução é o conjunto dos números reais
por um número real qualquer que podemos escolher. Se a equação se cumpre, saberemos então que a solução é o conjunto dos números reais  , no caso de não cumprir-se, então saberemos que não existe solução. Substituímos
, no caso de não cumprir-se, então saberemos que não existe solução. Substituímos  , assim
, assim
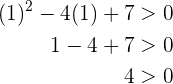
Como sabemos que  , então o conjunto solução é
, então o conjunto solução é  .
.
7 
Nossa inequação é:

Começamos a resolver o exercício
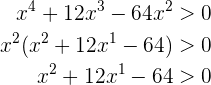
Note que ao final dividimos entre  , isto porque ao ser uma expressão estritamente positiva, é impossível que
, isto porque ao ser uma expressão estritamente positiva, é impossível que  , portanto
, portanto  . Agora, calculando as raízes de
. Agora, calculando as raízes de  podemos escrever nossa inequação como
podemos escrever nossa inequação como
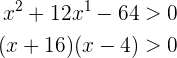
Isto quer dizer que  , no entanto, o produto é positivo unicamente quando as expressões que podem ser multiplicadas têm o mesmo sinal, isto é, temos dois casos principais, Um em que
, no entanto, o produto é positivo unicamente quando as expressões que podem ser multiplicadas têm o mesmo sinal, isto é, temos dois casos principais, Um em que 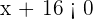 e
e 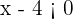 , e o outro em que
, e o outro em que  e
e  .
.
Avaliamos cada caso, começando pelo primeiro. Supomos que 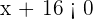 , então
, então 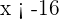 , além disso, sabemos que
, além disso, sabemos que 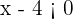 , então
, então 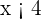 , isto é
, isto é  deve cumprir
deve cumprir 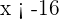 e
e 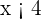 , ou seja, deve pertencer à interseção dos intervalos
, ou seja, deve pertencer à interseção dos intervalos  e
e  . Note que a interseção é
. Note que a interseção é  , portanto, esta é uma solução.
, portanto, esta é uma solução.
Agora passamos para o segundo caso. Suponhamos que  , então
, então  , além disso, sabemos que
, além disso, sabemos que  , então
, então  , isto quer dizer que
, isto quer dizer que  deve cumprir
deve cumprir  e
e  , ou seja, deve pertencer à interseção dos intervalos
, ou seja, deve pertencer à interseção dos intervalos  e
e  . Note que a interseção é
. Note que a interseção é  , este intervalo também é uma solução.
, este intervalo também é uma solução.
Assim, nossa solução final é a união das duas soluções individuais que encontramos, isto é, a solução final é  .
.

8 

Procedemos a resolver os exercícios
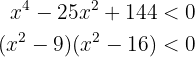
Isto quer dizer que 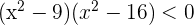 , no entanto, o produto é negativo unicamente quando as expressões que podem ser multiplicadas têm sinais opostos, isto é, temos dois casos principais. Um em que
, no entanto, o produto é negativo unicamente quando as expressões que podem ser multiplicadas têm sinais opostos, isto é, temos dois casos principais. Um em que  e
e 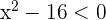 , e o outro em que
, e o outro em que 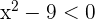 e
e  .
.
Avaliamos cada caso, começando pelo primeiro. Supomos que  . Primeiro, de novo, devemos expressar este polinômio de segunda ordem como produto de expressões do primeiro grau, isto é
. Primeiro, de novo, devemos expressar este polinômio de segunda ordem como produto de expressões do primeiro grau, isto é
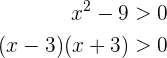
Para que isto seja positivo deve-se cumprir também que  e
e  sejam do mesmo sinal, isto é, que ambos sejam positivos ou ambos negativos. Supondo que ambos sejam negativos, sabemos que
sejam do mesmo sinal, isto é, que ambos sejam positivos ou ambos negativos. Supondo que ambos sejam negativos, sabemos que 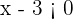 , então,
, então, 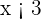 e
e  , então,
, então, 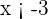 , isto é equivalente a dizer que
, isto é equivalente a dizer que  pertence à interseção dos intervalos
pertence à interseção dos intervalos  e
e  da qual é
da qual é  .
.
Agora supomos que  e
e  são positivos, sabemos que
são positivos, sabemos que  , então,
, então,  e
e  , então,
, então,  , isto é equivalente a dizer que
, isto é equivalente a dizer que  pertence à interseção dos intervalos
pertence à interseção dos intervalos  e
e  que é
que é  .
.
Assim, para que se cumpra  devemos saber que
devemos saber que  pertence à união dos dois intervalos que encontramos previamente, isto é, que
pertence à união dos dois intervalos que encontramos previamente, isto é, que  pertence a
pertence a  .
.
Como a suposição é de que  , e também sabemos que
, e também sabemos que 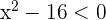 , devemos expressar este polinômio de segunda ordem como produto de expressões do primeiro grau, isto é
, devemos expressar este polinômio de segunda ordem como produto de expressões do primeiro grau, isto é
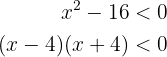
Para que isto seja positivo, deve-se cumprir também que  e
e  tenham sinais opostos. Supondo que
tenham sinais opostos. Supondo que 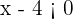 e
e  sabemos que
sabemos que 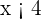 e
e  respectivamente, isto é,
respectivamente, isto é,  pertencem à interseção dos intervalos
pertencem à interseção dos intervalos  e
e  que é
que é  .
.
Agora supomos que  e
e 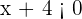 sabemos que
sabemos que  e
e  respectivamente, isto é,
respectivamente, isto é,  pertencem à interseção dos intervalos
pertencem à interseção dos intervalos  e
e  da qual é vazia. Assim, a única forma de que
da qual é vazia. Assim, a única forma de que 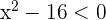 é quando
é quando  pertença ao intervalo
pertença ao intervalo 
Tudo até aqui nos diz que para que se cumpra  e
e 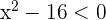 ,
,  deve pertencer à interseção dos conjuntos que encontramos,
deve pertencer à interseção dos conjuntos que encontramos,  e
e  , que é
, que é  .
.
Procedamos com nossa segunda suposição principal, que é 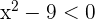 e
e  . Suponhamos que
. Suponhamos que 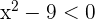 , primeiro, de novo, devemos expressar este polinômio de segunda ordem como produto de expressões do primeiro grau, isto é
, primeiro, de novo, devemos expressar este polinômio de segunda ordem como produto de expressões do primeiro grau, isto é
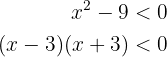
Para que isto seja negativo deve-se cumprir também que  e
e  tenham sinais opostos. Supondo que
tenham sinais opostos. Supondo que 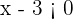 e
e  sabemos que
sabemos que 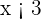 e
e  respectivamente, isto é,
respectivamente, isto é,  pertence à interseção dos intervalos
pertence à interseção dos intervalos  e
e  que é
que é  .
.
Agora supomos que  e
e  sabemos que
sabemos que  e
e 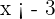 respectivamente, isto é,
respectivamente, isto é,  pertencem à interseção dos intervalos
pertencem à interseção dos intervalos  e
e  da qual é vazia. Assim, a única forma de que
da qual é vazia. Assim, a única forma de que 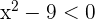 é quando
é quando  pertença ao intervalo
pertença ao intervalo 
Também sabemos que  , Devemos expressar este tipo de polinômio de segunda ordem como produto de expressões do primeiro grau, isto é
, Devemos expressar este tipo de polinômio de segunda ordem como produto de expressões do primeiro grau, isto é
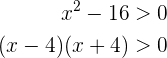
Para que isto seja positivo deve-se cumprir também que  e
e  tenham o mesmo sinal, isto é, que ambos sejam ou positivos ou negativos. Supondo que ambos são negativos, sabemos que
tenham o mesmo sinal, isto é, que ambos sejam ou positivos ou negativos. Supondo que ambos são negativos, sabemos que 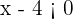 , então,
, então, 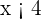 e
e 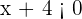 , então,
, então, 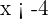 , isto é equivalente a dizer que
, isto é equivalente a dizer que  pertence à interseção dos intervalos
pertence à interseção dos intervalos  e
e  que é
que é  .
.
Agora supomos que  e
e  são positivos, sabemos que
são positivos, sabemos que  , então,
, então,  e
e  , então,
, então,  , isto é equivalente a dizer que
, isto é equivalente a dizer que  pertence à interseção dos intervalos
pertence à interseção dos intervalos  e
e  que é
que é  .
.
Assim, para que se cumpra que  devemos saber que
devemos saber que  pertence à união de dois intervalos que encontramos previamente, isto é,
pertence à união de dois intervalos que encontramos previamente, isto é,  que pertence à
que pertence à  .
.
Portanto, sabemos que para que se cumpra 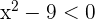 e
e  ,
,  deve pertencer à interseção dos conjuntos que encontramos,
deve pertencer à interseção dos conjuntos que encontramos,  e
e  , que é vazia.
, que é vazia.
Nossa solução final seria a união das duas soluções para cada caso, no entanto, como a última solução é o conjunto vazio, nossa solução final é o conjunto  .
.

9 
Resolveremos a seguinte inequação:

Note que

Para que a fração seja igual a zero deve-se cumprir que o numerador seja igual a zero, isto é  , portanto
, portanto  .
.
Sabemos que para que a fração seja estritamente negativa, deve-se cumprir que o numerador e o denominador tenham sinais opostos. Primeiro supomos que o numerador é positivo e o denominador negativo, portanto  , isto é
, isto é  e
e 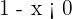 , portanto
, portanto  , isto quer dizer que
, isto quer dizer que  deve pertencer à interseção dos intervalos
deve pertencer à interseção dos intervalos  e
e  , que é
, que é  .
.
Agora supomos que o numerador é negativo e o denominador positivo, portanto 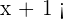 , isto é
, isto é 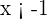 e
e  , portanto
, portanto  . Isto quer dizer que
. Isto quer dizer que  deve pertencer à interseção dos intervalos
deve pertencer à interseção dos intervalos  e
e  , que é
, que é  .
.
Tudo até aqui nos diz que para que se cumpra  , devemos saber que
, devemos saber que  deve pertencer à união dos dois intervalos que obtemos e o ponto
deve pertencer à união dos dois intervalos que obtemos e o ponto  . Portanto, o conjunto solução é
. Portanto, o conjunto solução é 

Resumir com IA:


