Bem-vindos à seção de Exercícios de Inequações de Primeiro Grau!
As inequações de primeiro grau são expressões algébricas que envolvem variáveis de primeira ordem e representam relações de desigualdade. Essas desigualdades são essenciais para modelar situações do mundo real em que as quantidades podem variar de forma contínua. Nesta série de exercícios, exploraremos o fascinante universo das inequações e sua aplicação na resolução de problemas práticos.
Ao longo desses exercícios, abordaremos conceitos importantes como a representação gráfica das inequações na reta numérica, a resolução de inequações simples e compostas, e a interpretação das soluções no contexto de situações do dia a dia. Esses problemas vão te ajudar a desenvolver habilidades fundamentais para compreender e trabalhar com inequações, uma ferramenta importante na álgebra e na modelagem de diferentes situações.

Inequações de uma variável
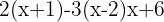
1 Retiramos os parênteses multiplicando o primeiro por  e o segundo por
e o segundo por  :
:
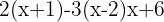
Agrupamos os termos semelhantes
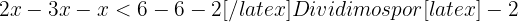 e mudamos o sentido da desigualdade
e mudamos o sentido da desigualdade


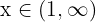
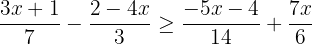
Determinamos o mínimo múltiplo comum dos denominadores para eliminar os denominadores
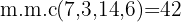
O número  é dividido por cada um dos denominadores, e o quociente obtido é multiplicado pelo numerador correspondente
é dividido por cada um dos denominadores, e o quociente obtido é multiplicado pelo numerador correspondente
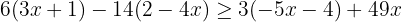
Retiramos os parênteses multiplicando o primeiro por  , o segundo por
, o segundo por 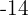 e o terceiro por
e o terceiro por  :
:

Agrupamos os termos semelhantes.
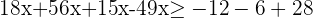
Reduzimos os termos semelhantes.
Simplificamos dividindo por 
Dividimos os dois membros por 
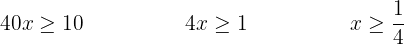

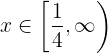
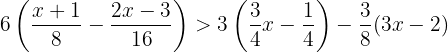
Retiramos os parênteses multiplicando o primeiro por  , o segundo por
, o segundo por  e o terceiro por
e o terceiro por 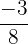 :
:
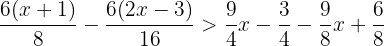
Determinamos o mínimo múltiplo comum dos denominadores para eliminar os denominadores
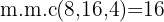
O número  é dividido por cada um dos denominadores, multiplicando-se o quociente obtido pelo numerador correspondente.
é dividido por cada um dos denominadores, multiplicando-se o quociente obtido pelo numerador correspondente.
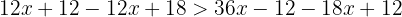
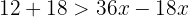
Agrupamos os termos, simplificamos dividindo por  e dividimos os dois membros por
e dividimos os dois membros por  .
.
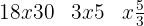
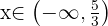
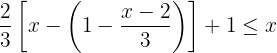
Removemos o colchete multiplicando por  , de modo que o colchete passa a ser um parêntese.
, de modo que o colchete passa a ser um parêntese.
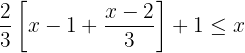
Retiramos os parênteses multiplicando por 
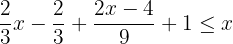
Determinamos o mínimo múltiplo comum para eliminar os denominadores.
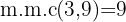
O número  é dividido por cada um dos denominadores, multiplicando-se o quociente obtido pelo numerador correspondente.
é dividido por cada um dos denominadores, multiplicando-se o quociente obtido pelo numerador correspondente.

Agrupamos os termos semelhantes e realizamos as somas e subtrações indicadas.
Como o coeficiente de  é negativo, multiplicamos por
é negativo, multiplicamos por  , de modo que o sentido da desigualdade se inverte.
, de modo que o sentido da desigualdade se inverte.


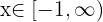
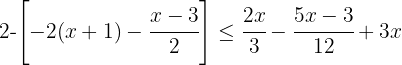
1º Retirar os colchetes.
Removemos o parêntese multiplicando por  , de modo que o colchete passa a ser um parêntese:
, de modo que o colchete passa a ser um parêntese:
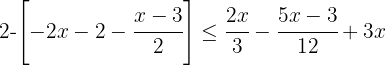
2º Retirar os parênteses.
Retiramos os parênteses multiplicando por  :
:

3º Eliminar os denominadores.
Determinamos o mínimo múltiplo comum:
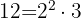
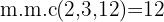
O número  é dividido por cada um dos denominadores, multiplicando-se o quociente obtido pelo numerador correspondente.
é dividido por cada um dos denominadores, multiplicando-se o quociente obtido pelo numerador correspondente.
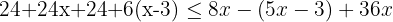
Retiramos os parênteses multiplicando o primeiro por  e o segundo por
e o segundo por  :
:

4º Agrupamos os termos em  de um lado da desigualdade e os termos independentes do outro.
de um lado da desigualdade e os termos independentes do outro.

5º Efetuamos as operações.
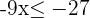
6º Se o coeficiente de  for negativo, multiplicamos por
for negativo, multiplicamos por  , de modo que o sentido da desigualdade se inverte.
, de modo que o sentido da desigualdade se inverte.
Este passo sempre deve ser feito antes de isolar a incógnita.

7º Isolamos a incógnita, dividindo ambos os membros por  .
.

Na prática, costuma-se dizer que o  está multiplicando e passa para o outro membro dividindo
está multiplicando e passa para o outro membro dividindo  .
.

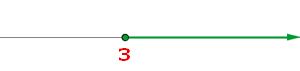
Obtemos a solução como uma desigualdade, mas ela também pode ser expressa:
De forma gráfica
Como um intervalo
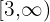
Calcule o valor indicado
Encontre os valores de  para os que as raízes da equação
para os que as raízes da equação 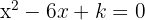 sejam as duas reais e distintas.
sejam as duas reais e distintas.
Para que a equação tenha duas raízes reais e distintas, o discriminante 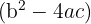 deve ser maior que zero.
deve ser maior que zero.
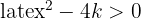
Resolvemos a inequação:
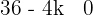
Multiplicamos por  e mudamos o sinal da desigualdade.
e mudamos o sinal da desigualdade.
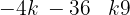

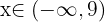
Encontre os valores de  para os que as raízes da equação
para os que as raízes da equação 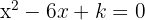 sejam as duas reais e distintas.
sejam as duas reais e distintas.
Para que a equação tenha duas raízes reais e iguais, o discriminante 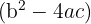 deve ser igual a zero.
deve ser igual a zero.
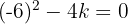
Resolvemos a equação:
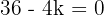
Multiplicamos por  e mudamos o sinal da igualdade.
e mudamos o sinal da igualdade.

Encontre os valores de  para os que as raízes da equação
para os que as raízes da equação 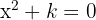 sejam as duas reais e distintas.
sejam as duas reais e distintas.
Para que a equação tenha duas raízes reais e distintas, o discriminante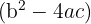
deve ser maior que zero.

Resolvemos a inequação:
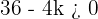
Multiplicamos por  e mudamos o sinal da desigualdade.
e mudamos o sinal da desigualdade.
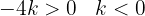
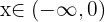
Encontre os valores de  para que as raízes da equação
para que as raízes da equação 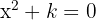 sejam imaginárias.
sejam imaginárias.
Para que a equação tenha duas raízes imaginárias, o discriminante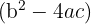
deve ser menor que zero.
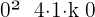
Resolvemos a inequação:
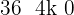
Multiplicamos por  e mudamos o sinal da desigualdade.
e mudamos o sinal da desigualdade.
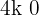
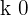
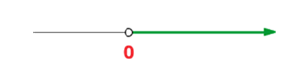

Encontre os valores de  para que as raízes da equação
para que as raízes da equação 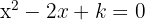 sejam imaginárias.
sejam imaginárias.
Precisamos que o discriminante satisfaça < 0.
< 0.
Ou seja, que:
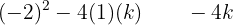
4 − 4k < 0
4 < 4k
1 < k
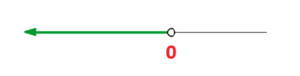
Ou seja, toda a reta k > 1 faz com que a equação não tenha raízes reais.
Inequações de duas variáveis


1º Transformamos a desigualdade em igualdade.

2º Atribuímos dois valores à variável x, com os quais obtemos dois pontos.


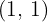

latex[/latex]
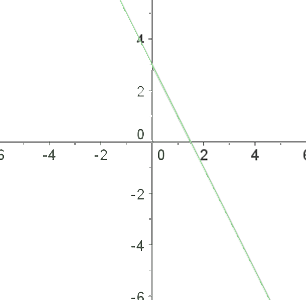
3º Ao representar e unir esses pontos, obtemos uma reta.
Tomamos o ponto latex[/latex] e o substituímos na inequação.

Como a desigualdade se cumpre, a solução é o semiplano onde está o ponto latex[/latex], incluindo a reta, porque consideramos os valores menores e também os iguais.
Neste caso, desenhamos a reta com traço contínuo.
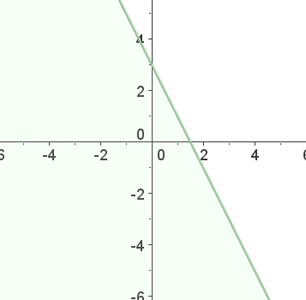
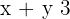
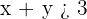
1º Transformamos a desigualdade em igualdade.
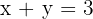
2º Atribuímos dois valores à variável x, com os quais obtemos dois pontos.


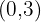



Tomamos o ponto latex[/latex] e o substituímos na inequação.

Como a desigualdade não se cumpre, a solução é o semiplano onde não está o ponto  , sem incluir a reta, porque pegamos os valores menores.
, sem incluir a reta, porque pegamos os valores menores.
Neste caso, desenhamos a reta com traço contínuo.
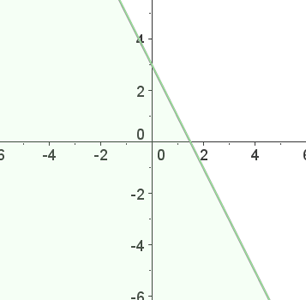
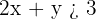
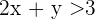
1º Transformamos a desigualdade em igualdade.

2º Atribuímos dois valores à variável  , com os quais obtemos dois pontos.
, com os quais obtemos dois pontos.


latex[/latex]


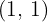
3º Ao representar e unir esses pontos, obtemos uma reta.
Tomamos o ponto  e o substituímos na inequação.
e o substituímos na inequação.

Como a desigualdade não se cumpre, a solução é o semiplano onde o ponto  não se encontra.
não se encontra.
Nesse caso (maior que, mas não igual), os pontos da reta não pertencem à solução.
Por isso, desenhamos a reta com traço descontínuo.

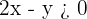
1º Transformamos a desigualdade em igualdade.
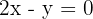
2º Damos à variável  dois valores, com os quais obtemos dois pontos.
dois valores, com os quais obtemos dois pontos.


latex[/latex]



Tomamos o ponto  e o substituímos na inequação.
e o substituímos na inequação.

Como a desigualdade não se cumpre, a solução é o semiplano onde o ponto  não se encontra.
não se encontra.
Nesse caso (maior que, mas não igual), os pontos da reta não pertencem à solução.
Neste caso desenhamos a reta com traço descontínuo.

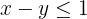
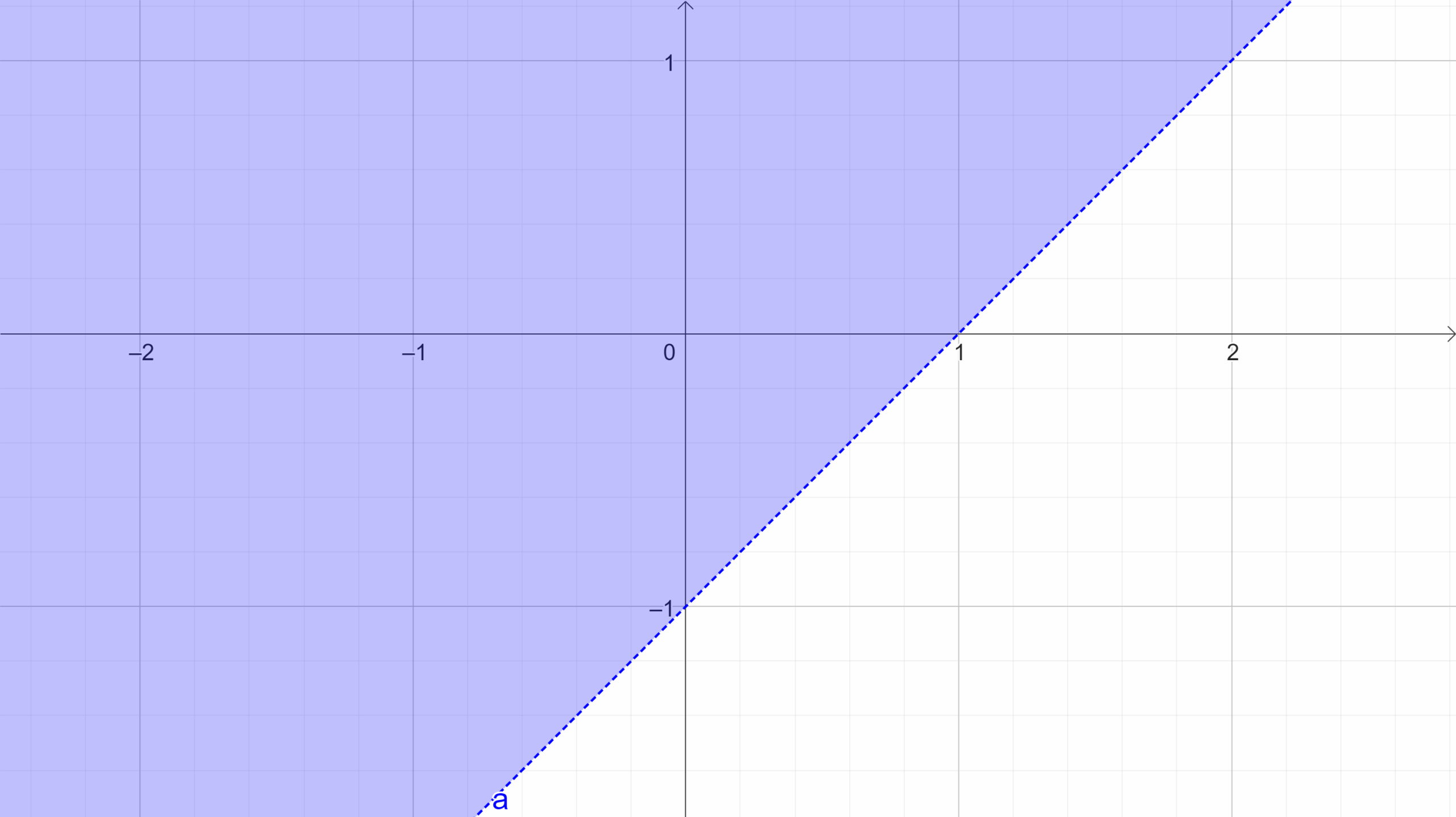
Ao isolar 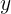 , obtemos a desigualdade
, obtemos a desigualdade  .
.
Lembrando que a reta 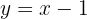 tem coeficiente angular igual a 1 e passa pelos pontos
tem coeficiente angular igual a 1 e passa pelos pontos 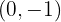 e
e 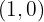 , essa desigualdade representa toda a região que fica acima dessa reta.
, essa desigualdade representa toda a região que fica acima dessa reta.
Resumir com IA:












