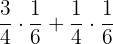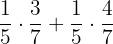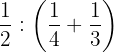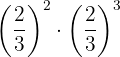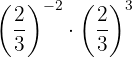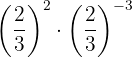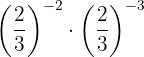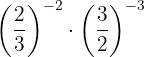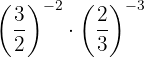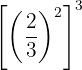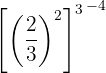Temas
Bem-vindo aos desafios empolgantes de operações com frações! Nesta série de exercícios matemáticos, vamos explorar o fascinante universo das frações e aprender a realizar diferentes operações com elas.
As frações são uma parte essencial da matemática e estão presentes no dia a dia, desde a cozinha e a construção até as finanças e a ciência. Durante essa prática, vamos dominar as operações fundamentais com frações, como soma, subtração, multiplicação e divisão.
Se você quer aprimorar suas habilidades matemáticas ou simplesmente reforçar seus conhecimentos, esses exercícios vão te ajudar a entender melhor como trabalhar com frações e aplicá-las em diversas situações do cotidiano.

Operações básicas com frações
Expresse cada uma das seguintes frações de hora em minutos:

Lembre-se de que  hora
hora 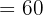 minutos. Portanto, para converter cada fração em minutos, podemos usar uma regra de três simples.
minutos. Portanto, para converter cada fração em minutos, podemos usar uma regra de três simples.
a. Conversão de 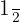 hora em minutos:
hora em minutos:
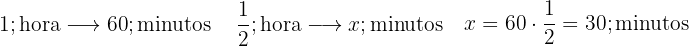
b. Conversão de  hora em minutos:
hora em minutos:
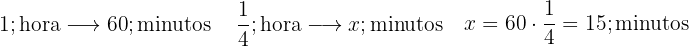
c Conversão de 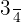 hora em minutos:
hora em minutos:
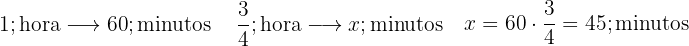
d. Conversão de  hora em minutos:
hora em minutos:
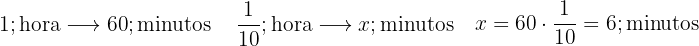
e. Conversão de  hora em minutos:
hora em minutos:
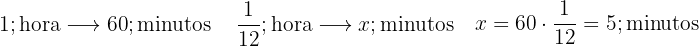
f. Conversão de  hora em minutos:
hora em minutos:
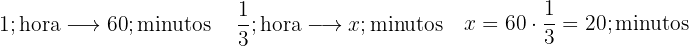
Encontre os pares de frações equivalentes e coloque-os em pares:
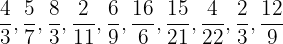
Para resolver este exercício, por praticidade utilizaremos a redução de frações. Assim, notemos que as frações:
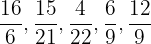 são redutíveis.
são redutíveis.
a. Reduzimos a fração 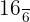 :
:
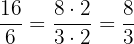
Portanto, o par equivalente da fração 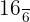 é
é 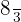 .
.
b. Reduzimos a fração 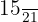 :
:
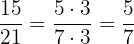
Portanto, o par equivalente da fração 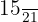 é
é 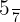 .
.
c. Reduzimos a fração 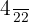 :
:
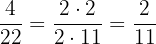
Portanto, o par equivalente da fração 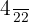 é
é 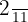 .
.
d. Reduzimos a fração  :
:
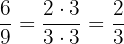
Portanto, o par equivalente da fração  é
é 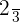 .
.
e. Reduzimos a fração 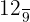 :
:
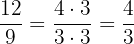
Portanto, o par equivalente da fração 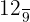 é
é 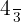 .
.
Escreva os inversos de: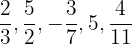
Primeiro, devemos lembrar que um número e seu inverso devem satisfazer a condição de que seu produto seja igual a 1.
O inverso  de
de 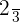 deve satisfazer que:
deve satisfazer que:
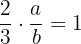 ,
,
portanto, 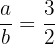 .
.
O inverso  de
de 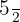 deve satisfazer que:
deve satisfazer que:
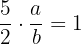 ,
,
portanto, 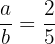 .
.
O inverso  de
de 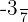 deve satisfazer que:
deve satisfazer que:
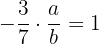 ,
,
portanto, 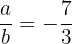 .
.
O inverso  de
de  deve satisfazer que:
deve satisfazer que:
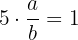 ,
,
portanto, 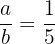 .
.
O inverso  de
de  deve satisfazer que:
deve satisfazer que:
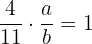 ,
,
portanto, 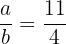 .
.
Compare as seguintes frações: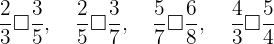
Para resolver este exercício, calculamos o denominador comum de cada par de frações comparadas.
Lembramos que, entre duas frações com denominadores iguais, a menor é aquela com o menor numerador. Assim, temos:
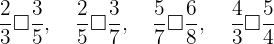
Calculando um denominador comum para cada caso, obtemos:
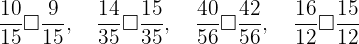
Portanto, as desigualdades são:
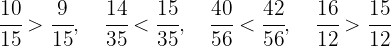
Ou seja:
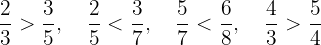
Compare as frações dadas e escreva o sinal 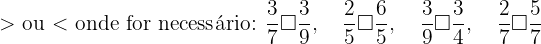
Para resolver este exercício, utilizamos dois princípios:
Entre duas frações com o mesmo numerador, a menor é aquela com o maior denominador.
Entre duas frações com o mesmo denominador, a menor é aquela com o menor numerador.
Seguindo esses critérios, obtemos:
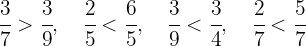
Ordene do menor para o maior: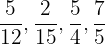
Primeiramente, precisamos calcular o MMC. dos denominadores para colocar as frações com um denominador comum. A menor fração será aquela com o menor numerador.
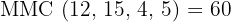
O mínimo múltiplo comum 60 indica que é um número divisível por cada um dos denominadores.
Reescrevemos cada uma das frações para obter frações equivalentes às iniciais, mas com denominador 60:

Desenvolva a seguinte operação de duas formas distintas: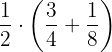
a. Aplicando primeiro a propriedade distributiva:
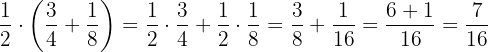
b. Resolvendo primeiro a soma:
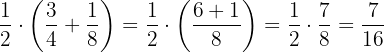
Calcule o resultado de cada uma das somas, utilizando a fatoração do fator comum:
Fatorar é o processo inverso da propriedade distributiva. Podemos transformar a soma em um produto extraindo o fator comum, ou seja:
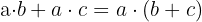
a. Para calcular 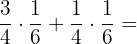 fatoramos
fatoramos 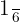 e depois resolvemos:
e depois resolvemos:
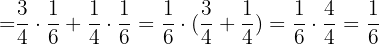
b. Para calcular 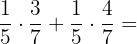 fatoramos
fatoramos  e depois resolvemos:
e depois resolvemos:
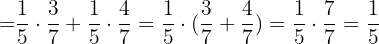
Classifique as seguintes frações em próprias ou impróprias: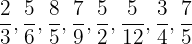
Para responder, lembramos de duas coisas:
As frações próprias têm o denominador maior que o numerador.
As frações impróprias têm o denominador menor que o numerador.
a. Frações próprias:
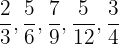
b. Frações impróprias:
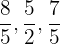
Calcule a soma das seguintes frações: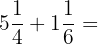
Reescrevemos e desenvolvemos a soma:
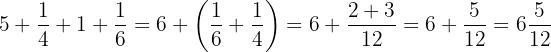
Conversões de números decimais para frações
Converter em fração as seguintes expressões decimais:
a. Conversão em fração de 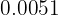 :
:
Sendo um número decimal exato, no numerador escrevemos o número sem a vírgula e no denominador a unidade seguida de 4 zeros, pois há 4 casas decimais, como mostrado a seguir:
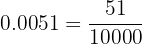
b. Conversão em fração de 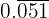 :
:
Sendo um número periódico puro, no numerador escrevemos o número sem a vírgula e no denominador 3 noves, pois há 3 dígitos periódicos:
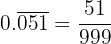 .
.
c. Conversão em fração de  :
:
Sendo um número periódico misto, no numerador escrevemos o número sem a vírgula e subtraímos a parte que fica fora do período. No denominador há um nove e dois zeros, pois temos um dígito no período e duas casas decimais:
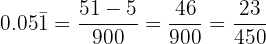
Converter em fração as seguintes expressões decimais: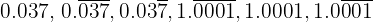
a. Conversão em fração de 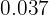 :
:
Sendo um número decimal exato, no numerador escrevemos o número sem a vírgula e no denominador a unidade seguida de 3 zeros, pois há 3 casas decimais:
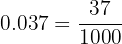
b. Conversão em fração de 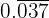 :
:
Sendo um número periódico puro, no numerador escrevemos o número sem a vírgula e no denominador 3 noves, pois há 3 dígitos periódicos:
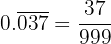
c. Conversão em fração de 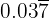 :
:
Sendo um número periódico misto, no numerador escrevemos o número sem a vírgula e subtraímos os números que estão fora do período. No denominador há um nove e dois zeros, pois temos um dígito no período e duas casas decimais:
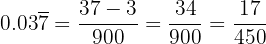
d. Conversão em fração de 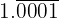 :
:
Sendo um número periódico puro, no numerador escrevemos o número sem a vírgula e subtraímos a parte que fica fora do período. No denominador, há 4 noves, pois há 4 dígitos periódicos:
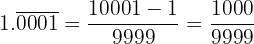
e. Conversão em fração de 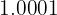 :
:
Sendo um número decimal exato, no numerador escrevemos o número sem a vírgula e no denominador a unidade seguida de 4 zeros, pois há 4 casas decimais:
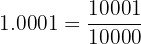
f. Conversão em fração de 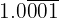 :
:
Sendo um número periódico misto, no numerador escrevemos o número sem a vírgula e subtraímos a parte fora do período. No denominador há 3 noves e um zero, pois temos três dígitos no período e uma casa decimal:
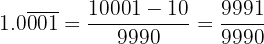
Operações com frações e dízimas periódicas
Realize as seguintes operações:
a. Para calcular a soma de:
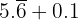 .
.
Primeiro, converteremos as dízimas periódicas em frações e, em seguida, realizaremos a soma:
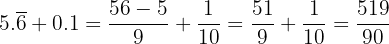
b. Para calcular:

Mais uma vez, converteremos as dízimas periódicas em frações e, em seguida, realizaremos a divisão:
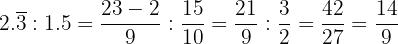
Resolva as seguintes operações com frações:
a. Resolvemos 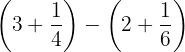 :
:
Removemos os parênteses; do lado direito da equação, como há o sinal de menos na frente, vamos trocar todos os sinais.
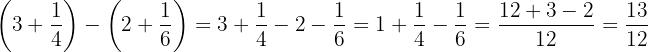
b. Resolvemos 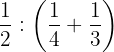
Primeiro, realizamos a soma dentro dos parênteses, depois dividimos as frações e, por último, simplificamos.
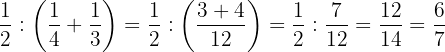
c. Resolvemos 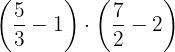
Realizamos as operações dentro dos parênteses, efetuamos o produto dos resultados e simplificamos.
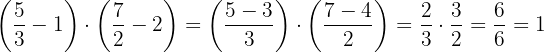
d. Resolvemos 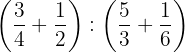 :
:
Realizamos as operações dentro dos parênteses, efetuamos a divisão dos resultados e simplificamos.
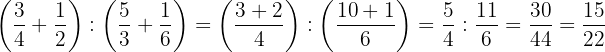
Efetue as seguintes divisões:
Para resolver cada uma das divisões, vamos lembrar que devemos multiplicar a primeira fração pelo inverso da segunda. Ou seja, multiplicamos os numeradores entre si e os denominadores entre si, obtendo assim o resultado da divisão:
a. 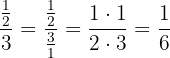
b. 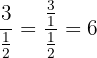
c. 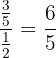
Realize as operações correspondentes:
a. Para calcular 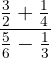 , primeiro realizamos as operações no numerador e denominador, simplificamos a fração resultante, realizamos a divisão e simplificamos novamente.
, primeiro realizamos as operações no numerador e denominador, simplificamos a fração resultante, realizamos a divisão e simplificamos novamente.
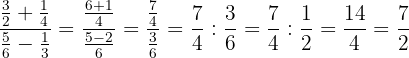
b. Para realizar a soma de 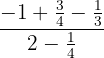 :
:
Faremos da mesma forma que no exercício anterior.
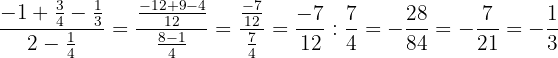 .
.
Efetue esta operação: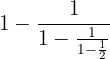
a. Primeiro, efetuamos 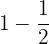 .
.
b. Fazemos o inverso de 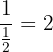 , obtendo o seguinte:
, obtendo o seguinte:
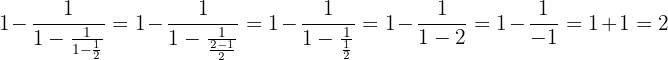
Realize as seguintes operações com potências:
a. Quando multiplicamos potências de mesma base, mantemos a base e somamos os expoentes:
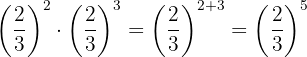
b. uando multiplicamos potências de mesma base, mantemos a base e subtraímos os expoentes:
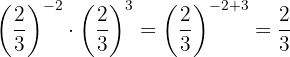
c. Quando multiplicamos potências de mesma base, mantemos a base e subtraímos os expoentes:
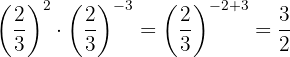
d. Quando multiplicamos potências de mesma base, mantemos a base e subtraímos os expoentes:
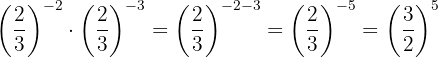
e. Realizamos o seguinte procedimento:
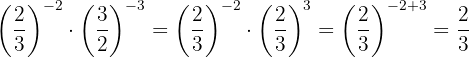
f. Precisamos dividir potências com a mesma base e subtraímos os expoentes:
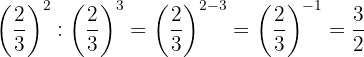
g. Fazemos um procedimento parecido ao anterior:
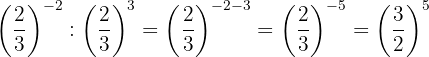
h. Outro vez, vamos fazer um procedimento semelhante ao anterior:
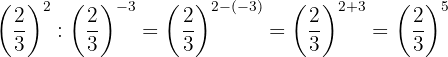
i. Fazemos um procedimento como o anterior:
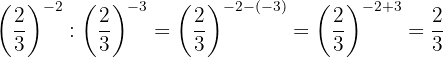
j. Mais uma vez, faremos uma operação semelhante ao anterior:
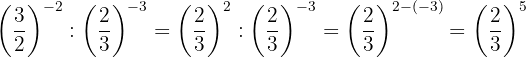
k. Lembrando que, para multiplicar potências com a mesma base, multiplicamos os expoentes:
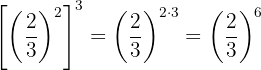
l. Aplicamos uma operação semelhante à do exercício anterior, utilizando a fração inversa para transformar o expoente negativo em positivo:
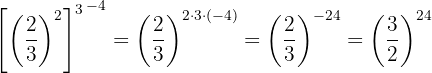
m. Vamos decompor os números em fatores primos. Dentro de cada parêntese, dividimos as bases das potências e mantemos o mesmo expoente. Veja como fazemos isso:
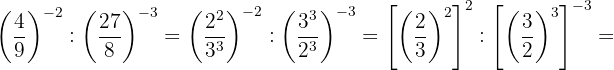
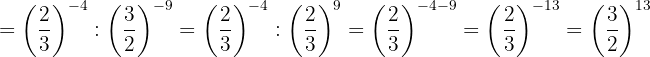
Efetue:
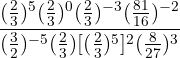
a. Vamos tentar colocar todas as frações com o mesmo numerador e denominador. Para isso, decompomos em fatores os números que não são primos:
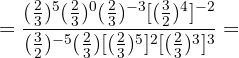
b. Para converter uma potência com expoente negativo em expoente positivo, devemos inverter a fração 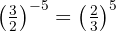 :
:
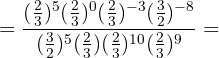
c. Novamente, aplicamos a inversão da fração com expoente positivo 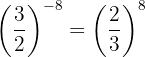 :
:
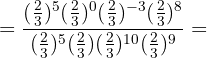
d. No numerador e no denominador, multiplicamos as potências de mesma base e realizamos a divisão dos resultados:
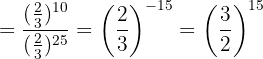
Desenvolva a seguinte operação:
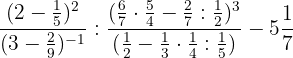
a. Realizamos as operações indicadas nos parênteses. No segundo denominador, devemos primeiro multiplicar e, no próximo passo, dividir.
O número misto 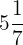 é reescrito com o mesmo denominador (7), somando o produto do número inteiro (5) pelo denominador (7) com o numerador da fração (1):
é reescrito com o mesmo denominador (7), somando o produto do número inteiro (5) pelo denominador (7) com o numerador da fração (1):
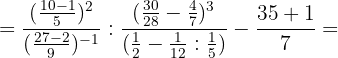
b. Efetuamos as operações indicadas e simplificamos 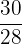 :
:
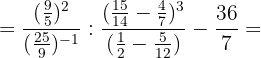
c. Realizamos as operações indicadas e reduzimos ao denominador comum na segunda fração:
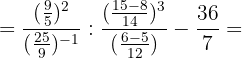
d. Efetuamos as operações na segunda fração e simplificamos:
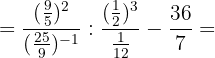
e. Aplicamos as potências e consideramos que, quando uma fração é elevada a um número negativo, devemos inverter o numerador e o denominador antes de elevar ao expoente:
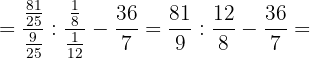
f. Simplificamos e resolvemos:
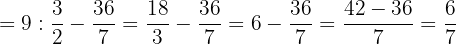
Resolva: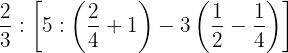
Efetuamos as operações nos dois parênteses: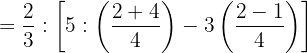
Como retiramos os parênteses, o colchete se transforma em parênteses: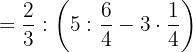
Realizamos a divisão e a multiplicação dentro do parênteses e simplificamos os resultados: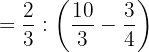
Dividimos 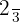 pelo resultado do parênteses e simplificamos:
pelo resultado do parênteses e simplificamos: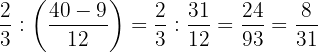
Calcule: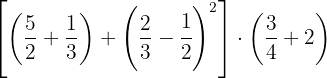
a. Realizamos as operações dentro dos parênteses: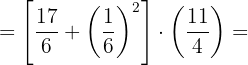
b. Calculamos a potência e substituímos o colchete por parênteses: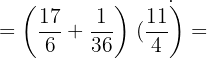
c. Resolvemos o primeiro parênteses: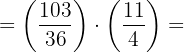
d. Fazemos a multiplicação e simplificamos: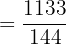
Efetue: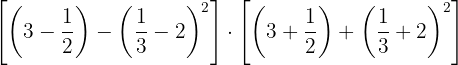
a. Operamos nos parênteses: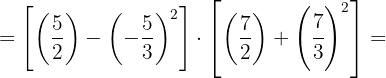
b. Calculamos as potências: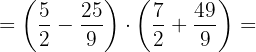
c. Realizamos as operações dentro dos parênteses: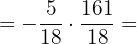
d. Fazemos a multiplicação e simplificamos o resultado: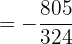
Resolva: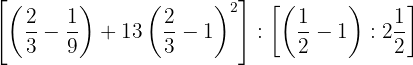
a. Transformamos o número misto 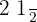 em fração. Mantemos o mesmo denominador (2) e o numerador é a soma da multiplicação da parte inteira (2) pelo denominador (2) mais o numerador do número misto (1).
em fração. Mantemos o mesmo denominador (2) e o numerador é a soma da multiplicação da parte inteira (2) pelo denominador (2) mais o numerador do número misto (1).
Reduzimos as frações de cada parêntese ao seu denominador comum.
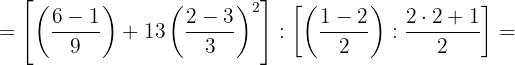
b. Realizamos as operações nos numeradores. Como dentro do segundo colchete removemos os parênteses, o colchete se transforma em parênteses: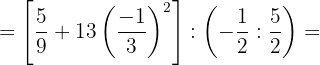
c. Calculamos a potência e, como não há mais parênteses no primeiro colchete, substituímos este por um parênteses:
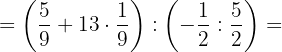
d. Multiplicamos no primeiro parêntese e dividimos no segundo: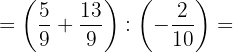
e. Somamos o primeiro parêntese, simplificamos no segundo e dividimos: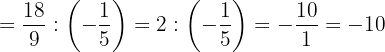
Efetue: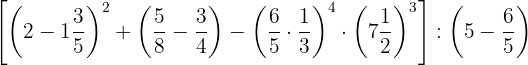
a. Primeiro realizamos os produtos e transformamos os números mistos em frações: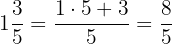
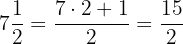
b. Substituímos os resultados: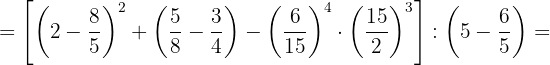
c. Operamos no primeiro parêntese, eliminamos o segundo, simplificamos no terceiro e operamos no último: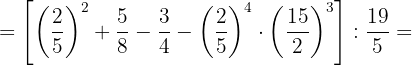
d. Realizamos a multiplicação e simplificamos, substituímos o colchete por um parênteses: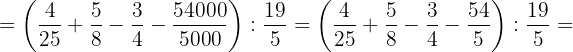
e. Realizamos as operações dentro do parênteses: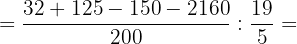
f. Finalizamos as operações no numerador, dividimos e simplificamos o resultado: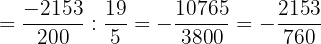
Resumir com IA: