Bem vindos a nossa página dedicada a exercícios de estatística. Elaboramos esta página para você ! Coloque à prova seus conhecimentos sobre estatística descritiva!
A estatística é uma disciplina relacionada com coletar, organizar, analisar e interpretar dados para extrair informação significativa e tomar decisões fundamentadas. Está baseada em métodos e técnicas matemáticas para recompilar informação numérica ou descritiva de uma população ou amostra em particular.
A estatística desempenha um papel crucial em uma ampla gama de campos, como a economia, a ciência, a saúde, a pesquisa de mercado e muitas outras áreas onde é necessário a análise de dados. Seu objetivo principal é de descobrir padrões, tendências e relações entre variáveis, o que permite compreender melhor o mundo que nos rodeia e a tomar boas decisões.
Neste espaço exploraremos os desafios e as soluções que surgem no fascinante mundo da estatística. Aqui exploraremos diferentes técnicas para analisar dados de maneira efetiva. Tais técnicas incluem calcular o desvio padrão, a variação, a mediana, média, moda, etc. de conjuntos de dados. O Superprof te convida a resolver os seguintes exercícios e problemas sobre estatística. Aperfeiçoe suas habilidades!
Em um conjunto de 
números cuja média é 
adicionamos os números 
e 
. Qual é a média do novo conjunto de números
A média do conjunto dos números é
Então
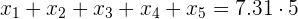
A média dos 
números é
Que é o mesmo que
Um dentista observa o número de cáries em cada um dos 
garotos de um colégio. A informação obtida aparece resumida na seguinte tabela:
| Nº de cáries |  |  |
|---|---|---|
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
- Complete a tabela obtendo os valores , , .
- Faça um gráfico de setores.
- Calcule o número médio de cáries.
a. Tabela
A soma das frequências relativas tem que ser igual a :
A frequência relativa de um dado é igual a sua frequência absoluta dividida por , que é a soma das frequências absolutas.
| Nº de cáries (xi) | | |  |
|---|---|---|---|
| | | |
| | | |
|  |  |  |
| | |  |
| | | |
|  |
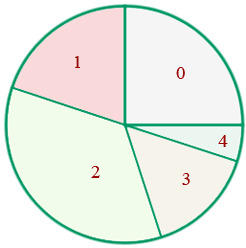
b. Gráfico de setores
Calculamos os graus que correspondem a uma unidade de frequência absoluta
Calculamos os graus que correspondem a cada frequência absoluta.
c. Média aritmética
Temos o seguinte conjunto de 
dados:
Obtenha a sua mediana e quartis.
1 Ordene os dados
Em primeiro lugar ordenamos os dados de menor para maior:
2 Mediana
Como o número de dados é par, a mediana é a média dos dois pontos centrais:
3 Quartis
Para obter o primeiro quartil, dividimos o número de dados por
Localizamos os números 
e em posição e encontramos a média
O segundo quartil é a mediana
Para o terceiro quartil, multiplicamos o número de dados por e depois dividimos por
Localizamos os números 
e em posição e encontramos a média
Um pediatra obteve a seguinte tabela com os meses de idade de 
crianças com o registro de quando elas andaram pela primeira vez:
| Meses | Crianças |
|---|---|
 | |
 | |
 | |
 |  |
 | |
 |  |
| |
- Desenhe o polígono de frequências.
- Calcule a moda, a mediana, a média e a variação
1 Polígono de frequências
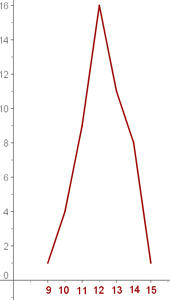
2 Complete a tabela
Completamos a tabela com:
A frequência acumulada 
para calcular a mediana.
O produto da variável pela sua frequência absoluta 
para calcular a média.
O produto da variável ao quadrado pela sua frequência absoluta 
para calcular a variação e o desvio típico.
 | |  | | |
|---|---|---|---|---|
| | | |  |
| | |  |  |
| | |  |  |
| |  |  |  |
| |  |  |  |
| |  |  |  |
| | | |  |
|  |  |
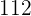3 Moda
A moda é o valor que tem maior frequência absoluta
Observamos na coluna das e a maior frequência absoluta 
corresponde a
4 Mediana
Para calcular a mediana dividimos 
por e vemos que a caixa das onde está corresponde a
5 Média aritmética
Calculamos a somatória da variável por sua frequência absoluta 
que é e dividimos por 
6 Variação
Calculamos a somatória de 
, dividimos por e subtraímos do resultado a média aritmética ao quadrado 
Complete os dados que faltam na seguinte tabela estatística:
| | | |
|---|---|---|---|
| |  | |
| | ||
| |  | |
| |  | |
| |  | |
|  | ||
| | | |
|
1 Tabela
Primeira fileira
A primeira frequência acumulada coincide com a primeira frequência absoluta
A primeira frequência relativa acumulada 
é igual a primeira frequência absoluta 
dividida por 
Então é o número total de dados
Segunda fileira
A segunda frequência acumulada será igual à frequência acumulada anterior mais a frequência absoluta correspondente
A frequência relativa acumulada 
é igual à frequência absoluta dividida por
Terceira fileira
Para encontrar a frequência absoluta podemos fazer de duas maneiras
1. Por meio da frequência relativa acumulada:
2. A frequência absoluta será a diferença entre 
e 
Quarta fileira
A frequência acumulada será igual à frequência acumulada anterior mais a frequência absoluta correspondente 
Quinta fileira
A frequência relativa acumulada 
é igual a frequência absoluta 
dividida por
Sexta fileira
De maneira análoga à terceira fileira, temos dois modos de fazer
A frequência absoluta será igual à frequência acumulada 
menos a frequência acumulada anterior 
, isto é, a diferença entre 
e 
A frequência relativa acumulada 
é igual à frequência absoluta 
dividida por
Sétima fileira
A frequência relativa acumulada 
é igual à frequência absoluta dividida por
Oitava fileira
A última frequência acumulada coincide com
A frequência absoluta será igual à frequência acumulada 
menos a frequência acumulada anterior 
, isto é, a diferença entre 
e 
A frequência relativa acumulada 
é igual à frequência absoluta dividida por
2 Complete a tabela
Com os dados obtidos completamos a tabela. Além disso, adicionamos a coluna do produto da variável por sua frequência absoluta para calcular a média
| | | |  |
|---|---|---|---|---|
| | | | |
| | | | |
| | | |  |
| |  | | |
| | |  | |
| | | |  |
| | | | |
| | | | |
|  |
3 Média aritmética
Calculamos a somatória da variável por sua frequência absoluta 
que é e dividimos por
4 Mediana
Para calcular a mediana dividimos entre e vemos que a caixa das onde está corresponde a
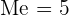
5 Moda
A moda é o valor que tem maior frequência absoluta
Consultamos a coluna das e a frequência absoluta maior corresponde a
Considere os seguintes dados: 
. Pede-se:
- Calcule sua média e sua variação.
- Se multiplicamos todos os dados anteriores por 3, qual será a nova média e variação.
Calcule sua média e sua variação
1 Média
Ordenamos os dados
.
Somamos os valores e dividimos entre o número total de dados que há.
2 Variação
Pegamos a média dos quadrados dos números e subtraímos o quadrado da média
Ao multiplicar por ...
1 Média
Se todos os valores da variável são multiplicados por a média aritmética fica multiplicada por
2 Variação
Se todos os valores da variável são multiplicados por a variação fica multiplicada por ao quadrado
O resultado ao lançar dois dados 
vezes está descrito na seguinte tabela:
| Somas | Vezes |
|---|---|
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
- Calcule a média e o desvio típico.
- Encontre a porcentagem de valores compreendidos no intervalo
.
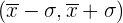1 Complete a tabela
Completamos a tabela com:
O produto da variável pela sua frequência absoluta para calcular a média.
O produto da variável ao quadrado pela sua frequência absoluta para calcular o desvio típico.
| | |  |
|---|---|---|---|
| | | |
| | |  |
| |  |  |
| |  |  |
| | |  |
| |  |  |
| |  |  |
| |  |  |
| |  |  |
| |  |  |
| |  |  |
|  |  |
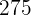2 Média aritmética
Adicionamos a coluna
porque queremos encontrar a sua somatória 
, que logo dividiremos por 
para obter a média 
3 Desvio típico
Adicionamos a coluna porque queremos encontrar a sua somatória 
, que logo dividiremos por 
depois subtraímos o resultado pela média aritmética ao quadrado 
, e por último faremos a raiz quadrada do resultado obtido
4 Porcentagem
Conhecendo o desvio típico, calculamos o intervalo mencionado.
Os valores compreendidos no intervalo 
são os correspondentes às somas de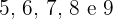 
. Somamos suas frequências absolutas.
Encontramos a porcentagem mediante a seguinte proporção:
As alturas de dois jogadores de uma equipe de basquete está dada na seguinte tabela:
| Altura | Nº de jogadores |
|---|---|
 | |
 | |
 | |
 | |
 | |
 | |
Calcule:
- A média.
- A mediana.
- O desvio típico.
- Quantos jogadores encontram-se acima da média mais um desvio típico?
1 Complete a tabela
Completamos a tabela com:
A frequência acumulada para calcular a mediana
O produto da variável pela sua frequência absoluta para calcular a média
O produto da variável ao quadrado pela sua frequência absoluta 
para calcular a variação e o desvio típico
| | | | | |
|---|---|---|---|---|---|
 |  | | | |  |
 |  | | |  |  |
 |  | | |  |  |
 |  | | | |  |
 |  | |  |  |  |
 |  | | |  |  |
|  |  |
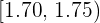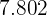2 Média
Calculamos a somatória da variável pela sua frequência absoluta que é e dividimos por 
3 Mediana
Devemos procurar o intervalo onde encontra-se a mediana. Para isso dividimos a por porque a mediana é o valor central
Procuramos na coluna das frequências acumuladas o intervalo que contém 
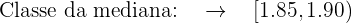
Aplicamos a fórmula para o cálculo da mediana para dados agrupados extraindo os seguintes dados:
Deste modo a mediana é
4 Desvio típico
Calculamos a somatória de 
, dividimos por 
e subtraímos o resultado pela média aritmética ao quadrado 
. Por último fazemos a raiz quadrada do resultado
Deste modo
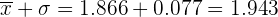
Este valor pertence a um percentil que encontra-se no penúltimo intervalo.
Estabelecemos a seguinte proporção:
Há apenas 3 jogadores acima de 
Os resultados ao lançar um dado 200 vezes pode ser visto na seguinte tabela:
| | | | | | |
|---|---|---|---|---|---|---|
|  |  | |  |  | |
Determine e sabendo que a pontuação média é 
.
1 Complete a tabela
Realizamos a somatória de e de
| | |
|---|---|---|
| | |
| |  |
| |  |
| |  |
| |  |
| |  |
 |  |
2 Obtenha as equações
A somatória das frequências absolutas é igual a 
Com isso podemos concluir que
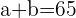
A somatória dos dividida por 
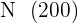é a média
Com o qual podemos concluir que
3 Resolvemos o sistema
Resolvemos o sistema de equações por redução
Finalmente
O histograma da distribuição correspondente ao peso de alunos de bacharelado é a seguinte:
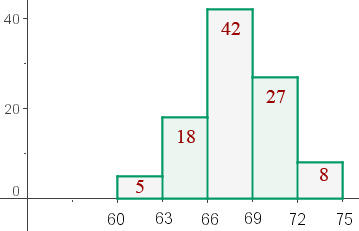
- Forme a tabela de distribuição.
- Se André pesa kg, então quantos alunos menos pesados que ele há?
- Calcule a moda.
- Encontre a mediana.
- A partir de quais valores encontram-se os
dos alunos mais pesados?
1 Tabela de distribuição
| | | |
|---|---|---|---|
 |  | | |
 |  |  | |
 |  |  |  |
 |  |  |  |
 |  | | |
|
2 Alunos menos pesados que André
Notamos que os primeiros quatro intervalos constituem de alunos menos pesados que André, assim, somamos suas frequências absolutas 
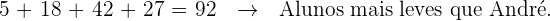
3 Moda
Em primeiro lugar, procuramos o intervalo onde encontra-se a moda, que será o intervalo que tenha a maior frequência absoluta
A classe modal é:
Aplicamos a fórmula para o cálculo da moda para dados agrupados extraindo os seguintes dados:
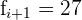
Assim, a moda é igual a
4 Mediana
Procuramos o intervalo onde encontra-se a mediana, para isso dividimos a por porque a mediana é o valor central
Procuramos na coluna das frequências acumuladas o intervalo que contém em
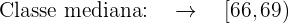
Aplicamos a fórmula para o cálculo da mediana para dados agrupados extraindo os seguintes dados:
Calculamos assim a mediana
5 Quartil terceiro
O valor a partir do qual encontra-se os dos alunos mais pesados é o quartil terceiro.
Procuramos o intervalo onde encontra-se o terceiro quartil, multiplicando por 
e dividindo por
Procuramos na coluna das frequências acumuladas o intervalo que contém em 
A classe de 
é:
Aplicamos a fórmula para o cálculo de quartis para dados agrupados extraindo os seguintes dados:
Assim, o terceiro quartil é igual a
Desta distribuição de frequências absolutas acumuladas, calcule:
| Idade | |
|---|---|
 | |
 | |
 | |
 |  |
 | |
- Média aritmética e desvio típico.
- Entre quais valores encontram-se as 10 idades centrais?
- Represente o polígono de frequências absolutas acumuladas.
1 Complete a tabela
Adicionamos a coluna das frequências absolutas
A primeira frequência absoluta coincide com a primeira frequência acumulada. Para calculá-las temos que subtrair da seguinte frequência absoluta sua anterior
| | | | | |
|---|---|---|---|---|---|
| | | | | |
| | | | |  |
| | | | |  |
| | | | |  |
| | | |  |  |
|  |  |
2 Média
Adicionamos a coluna porque queremos encontrar sua somatória 
, que logo dividiremos por 
para obter a média
3 Desvio típico
Adicionamos a coluna 
porque queremos encontrar sua somatória 
, que logo dividiremos por 
e subtraímos o seu resultado pela média aritmética ao quadrado 
, e por último faremos a raiz quadrada do resultado obtido
4 Idades centrais
Podemos ver que a porcentagem representa as idades
Os alunos representam os centrais da distribuição.
Devemos encontrar 
e 
.
As idades centrais estão no intervalo: 
.
5 Polígono de frequências
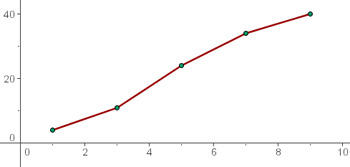
Uma pessoa 
mede 
m e mora em uma cidade onde a estatura média é de 
m e o desvio típico é de cm. Outra pessoa
mede 
m e mora em uma cidade onde a estatura média é de 
m e o desvio típico é de cm. Qual dos dois será mais alto em relação aos outros moradores?
Obtemos as pontuações típicas destas pessoas na distribuição correspondente
É importante trabalhar com as mesmas unidades, assim, a altura será considerada em centímetros
A pontuação típica da primeira pessoa é:
A pontuação típica da segunda pessoa é:
Ao comparar suas pontuações, concluímos que a pessoa é mais alta em relação aos outros moradores do que a pessoa .
Um professor fez dois testes em um grupo de alunos, obtendo assim os seguintes resultados: para o primeiro teste a média é e o desvio típico 
.
Para o segundo teste a média é e o desvio típico 
.
Um aluno obtém um no primeiro e um no segundo. Em relação com o grupo, qual dos dois testes obteve uma melhor pontuação?
Obtemos as pontuações típicas deste aluno nas distribuições de cada teste
A pontuação típica no primeiro teste é:
A pontuação típica no segundo teste é:
Ao comparar as pontuações, notamos que no segundo teste ele consegue uma maior pontuação.
O número de espectadores nas salas de um cinema em um determinado dia foi de 
e 
pessoas.
- Calcule a dispersão do número de espectadores.
- Calcule o coeficiente de variação.
- Se neste dia aparecem pessoas a mais em cada sala, qual efeito isso causaria na dispersão?
1 Desvio típico
Obtemos a média aritmética
Finalmente calculamos o desvio típico
2 Coeficiente de variação
Para calcular o coeficiente de variação devemos dividir o desvio típico pela média aritmética
3 Dispersão com 50 pessoas a mais
Se todas as salas têm um incremento de pessoas, a média aritmética também será incrementada em pessoas. Então,
O desvio típico não varia, já que somamos a mesma quantidade a cada dado da série.
A dispersão relativa é menor no segundo caso.
Considere o seguinte conjunto de dados
- Calcule a moda.
- Calcule a média.
- Calcule a mediana.
- Calcule os quartis.
- Calcule o desvio típico.
Primeiro ordenamos os dados em ordem ascendente:
1Moda
A moda é o elemento que mais se repete no nosso conjunto de dados. Assim, a moda é
2 Mediana
Obtemos a média aritmética
3 Mediana
A mediana é o dado que separa o conjunto em duas partes iguais. Por ter um conjunto com um número ímpar de dados, a mediana corresponderá ao dado central, que neste caso é
4 Quartis
Para calcular os quartis usaremos a fórmula para um conjunto com um número de elementos ímpar
onde 
é o número de elementos no conjunto, neste caso 
Esta fórmula nos dá a posição do quartil.
,
então o primeiro quartil encontra-se na quarta posição do nosso conjunto ordenado de dados, neste caso, 
,
então o segundo quartil encontra-se na oitava posição do nosso conjunto ordenado de dados, neste caso, 
De fato, sempre 
,
então o terceiro quartil encontra-se na duodécima posição do nosso conjunto ordenado de dados, neste caso, 
4 Desvio típico
Para calcular o desvio típico, 
usamos a fórmula
onde é o número de dados e são os dados do conjunto, 
. No nosso caso, 
e 
. Assim, temos
Ainda restam dúvidas? E que tal procurar um professor de matemática?
Gostou desse artigo? Deixe uma nota!
Loading...
