A estatística é uma ferramenta essencial para a análise e interpretação de dados em diversas áreas, desde as ciências sociais até a engenharia. Compreender os conceitos estatísticos e saber aplicá-los corretamente é fundamental para tomar decisões com base em dados.
Esta seção de exercícios resolvidos foi desenvolvida para reforçar o aprendizado teórico dos principais tópicos da estatística. Por meio da prática com problemas reais, o objetivo é aprimorar as habilidades analíticas e fortalecer a capacidade de solucionar desafios estatísticos, tanto os mais comuns quanto os mais complexos.
Indique quais variáveis são qualitativas e quais são quantitativas:
- Comida favorita.
- Profissão que você gosta.
- Número de gols marcados pelo seu time favorito na última temporada.
- Número de alunos do seu colégio.
- A cor dos olhos dos seus colegas de classe.
- Coeficiente intelectual dos seus colegas de classe.
a. Comida favorita.
Qualitativa
b. Profissão que você gosta.
Qualitativa
c. Número de gols marcados pelo seu time favorito na última temporada.
Quantitativa
d. Número de alunos do seu colégio.
Quantitativa
e. A cor dos olhos dos seus colegas de classe.
Qualitativa
f. Coeficiente intelectual dos seus colegas de classe.
Quantitativa
Das seguintes variáveis, indique quais são discretas e quais são contínuas:
- Número de ações vendidas por dia na Bolsa de Valores.
- Temperaturas registradas a cada hora em um observatório.
- Tempo de duração de um automóvel.
- O diâmetro das rodas de vários carros.
- Número de filhos de
 famílias.
famílias. - Censo anual da população brasileira.
a. Número de ações vendidas por dia na Bolsa de Valores.
Discreta
b. Temperaturas registradas a cada hora em um observatório.
Contínua
c. Tempo de duração de um automóvel.
Contínua
d. O diâmetro das rodas de vários carros.
Contínua
e. Número de filhos de  famílias.
famílias.
Discreta
f. Censo anual da população brasileira.
Discreta
Classifique as seguintes variáveis como qualitativas ou quantitativas e como discretas ou contínuas:
- A nacionalidade de uma pessoa.
- O número de litros de água contidos em um reservatório.
- O número de livros em uma estante de livraria.
- A soma de pontos obtidos no lançamento de um par de dados.
- A profissão de uma pessoa.
- A área dos diferentes azulejos de um edifício.
a. A nacionalidade de uma pessoa.
Qualitativa
b. O número de litros de água contidos em um reservatório.
Quantitativa e contínua
c. O número de livros em uma estante de livraria.
Quantitativa e discreta
d. A soma de pontos obtidos no lançamento de um par de dados.
Quantitativa e discreta
e. A profissão de uma pessoa.
Qualitativa
f. A área dos diferentes azulejos de um edifício.
Quantitativa e contínua
As pontuações obtidas por um grupo em uma prova foram:

Construa a tabela de distribuição de frequências e desenhe o polígono de frequências.
Passo a passo para construir a tabela de distribuição de frequências e desenhe o polígono de frequências.
 | Contagem |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |
- Na quarta coluna, colocamos a frequência acumulada
 .
. - Na primeira célula, inserimos a primeira frequência absoluta.
- Na segunda célula, somamos o valor da frequência acumulada anterior à frequência absoluta correspondente, e assim sucessivamente até a última, que deve ser igual a
 .
. - Na quinta coluna, registramos as frequências relativas,
 , que são obtidas dividindo cada frequência absoluta por
, que são obtidas dividindo cada frequência absoluta por  .
. - Na sexta coluna, colocamos a frequência relativa acumulada
 .
. - Na primeira célula, inserimos a primeira frequência relativa.
- Na segunda célula, somamos o valor da frequência relativa acumulada anterior à frequência relativa correspondente, e assim sucessivamente até a última, que deve ser igual a
 .
.
Polígono de frequências
No eixo das abscissas, representamos os dados, e no eixo das ordenadas, as frequências absolutas.
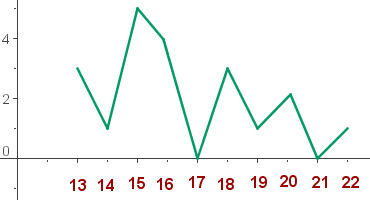
O número de estrelas dos hotéis de uma cidade é dado pela seguinte classificação:

Construa a tabela de distribuição de frequências e desenhe o diagrama de barras.
Passos para construir a tabela de distribuição de frequências e desenhar o diagrama de barras.
 | Contagem |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |
- Na quarta coluna, colocamos a frequência acumulada
 .
. - Na primeira célula, inserimos a primeira frequência absoluta.
- Na segunda célula, somamos o valor da frequência acumulada anterior à frequência absoluta correspondente, e assim sucessivamente até a última, que deve ser igual a
 .
. - Na quinta coluna, registramos as frequências relativas (
 ), que são obtidas dividindo cada frequência absoluta por
), que são obtidas dividindo cada frequência absoluta por  .
. - Na sexta coluna, colocamos a frequência relativa acumulada
 .
. - Na primeira célula, inserimos a primeira frequência relativa.
- Na segunda célula, somamos o valor da frequência relativa acumulada anterior à frequência relativa correspondente, e assim sucessivamente até a última, que deve ser igual a
 .
.
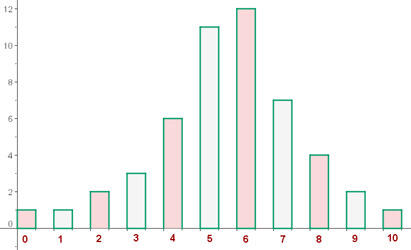
Diagrama de barras
No eixo das abscissas, representamos os dados, e no eixo das ordenadas, as frequências absolutas.
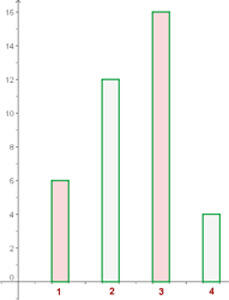
As notas de  alunos foram as seguintes:
alunos foram as seguintes:

Construa a tabela de distribuição de frequências e desenhe o diagrama de barras.
Esses são os passos para construir a tabela de distribuição de frequências e desenhar o diagrama de barras.
 |  |  |  |  |
 |  |  |  |  |
 1 1 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |
- Na quarta coluna, colocamos a frequência acumulada
 .
. - Na primeira célula, inserimos a primeira frequência absoluta.
- Na segunda célula, somamos o valor da frequência acumulada anterior à frequência absoluta correspondente, e assim sucessivamente até a última, que deve ser igual a
 .
. - Na quinta coluna, registramos as frequências relativas (
 ), que são obtidas dividindo cada frequência absoluta por
), que são obtidas dividindo cada frequência absoluta por  .
. - Na sexta coluna, colocamos a frequência relativa acumulada
 .
. - Na primeira célula, inserimos a primeira frequência relativa.
- Na segunda célula, somamos o valor da frequência relativa acumulada anterior à frequência relativa correspondente, e assim sucessivamente até a última, que deve ser igual a
 .
.
Diagrama de barras
No eixo das abscissas, representamos os dados, e no eixo das ordenadas, as frequências absolutas.
O peso de cada um dos  funcionários de uma fábrica são apresentados na seguinte tabela:
funcionários de uma fábrica são apresentados na seguinte tabela:
| Peso |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
A) Construa a tabela de frequências.
B) Represente o histograma e o polígono de frequências.
A) Tabela de frequências
 |  |  |  |  | |
 |  |  |  |  |  |
 |  |  |  |  | 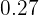 |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |
- Na quarta coluna, colocamos a frequência acumulada
 .
. - Na primeira célula, inserimos a primeira frequência absoluta.
- Na segunda célula, somamos o valor da frequência acumulada anterior à frequência absoluta correspondente, e assim sucessivamente até a última, que deve ser igual a
 .
. - Na quinta coluna, registramos as frequências relativas (
 ), que são obtidas dividindo cada frequência absoluta por
), que são obtidas dividindo cada frequência absoluta por  .
. - Na sexta coluna, colocamos a frequência relativa acumulada
 .
. - Na primeira célula, inserimos a primeira frequência relativa.
- Na segunda célula, somamos o valor da frequência relativa acumulada anterior à frequência relativa correspondente, e assim sucessivamente até a última, que deve ser igual a
 .
.
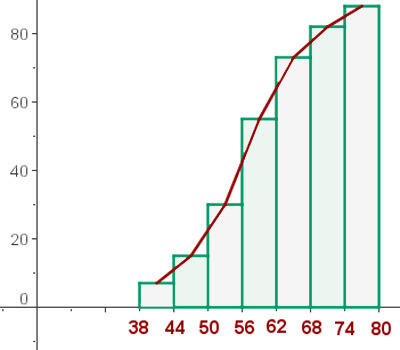
B) Representar o histograma e o polígono de frequências
Histograma
O polígono de frequências é construído unindo os pontos médios de cada retângulo.
Os  alunos de uma turma obtiveram as seguintes pontuações, em um total de
alunos de uma turma obtiveram as seguintes pontuações, em um total de  pontos, em um exame de Física:
pontos, em um exame de Física:

A) Construa a tabela de frequências.
B) Desenhe o histograma e o polígono de frequências.
A) Construa a tabela de frequências.
 |  |  |  |  | |
 |  |  |  |  |  |
 |  |  |  |  | 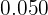 |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  | 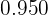 |
 |  |  |  | 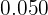 |  |
 |  |
- Na quarta coluna, colocamos a frequência acumulada
 .
. - Na primeira célula, inserimos a primeira frequência absoluta.
- Na segunda célula, somamos o valor da frequência acumulada anterior à frequência absoluta correspondente, e assim sucessivamente até a última, que deve ser igual a
 .
. - Na quinta coluna, registramos as frequências relativas (
 ), que são obtidas dividindo cada frequência absoluta por
), que são obtidas dividindo cada frequência absoluta por  .
. - Na sexta coluna, colocamos a frequência relativa acumulada
 .
. - Na primeira célula, inserimos a primeira frequência relativa.
- Na segunda célula, somamos o valor da frequência relativa acumulada anterior à frequência relativa correspondente, e assim sucessivamente até a última, que deve ser igual a
 .
.
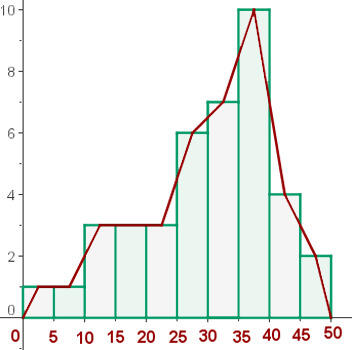
B) Desenhe o histograma e o polígono de frequências.
Histograma
O polígono de frequências é construído unindo os pontos médios de cada retângulo.
Considere uma distribuição estatística que é dada pela seguinte tabela:
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
Calcule:
- A moda, a mediana e a média.
- A amplitude, desvio médio, a variância e o desvio padrão.
Completamos a tabela com:
- A frequência acumulada (
 ) para calcular a mediana.
) para calcular a mediana. - O produto da variável pela sua frequência absoluta (
 ) para calcular a média.
) para calcular a média. - A diferença em relação à média
 e seu produto pela frequência absoluta
e seu produto pela frequência absoluta  para calcular o desvio médio.
para calcular o desvio médio. - O produto do quadrado da variável pela sua frequência absoluta (
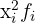 ) para calcular a variância e o desvio padrão.
) para calcular a variância e o desvio padrão.
 |  |  |  |  |  | 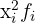 |
 |  |  |  |  |  |  |
 |  |  |  |  |  | 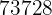 |
 |  |  |  | 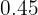 |  |  |
 |  |  |  |  |  |  |
 |  |  |  |  |  |  |
 |  |  |  |
Moda
A moda é o valor que possui a maior frequência absoluta.
Observamos a coluna das  e a maior frequência absoluta,
e a maior frequência absoluta,  , corresponde a
, corresponde a  .
.
 .
.
Mediana
Para calcular a mediana, dividimos  por
por  e verificamos a célula das
e verificamos a célula das  onde a
onde a  mais próxima de
mais próxima de  é
é  , que corresponde a
, que corresponde a  .
.


Média
Calculamos a soma do produto da variável pela sua frequência absoluta ( ), que é
), que é  , e dividimos por
, e dividimos por  .
.

Desvio médio
Calculamos a soma dos produtos das diferenças em relação à média pelas suas frequências absolutas correspondentes  , que é
, que é  , e dividimos por
, e dividimos por  .
.

Amplitude (Intervalo)
Realizamos a diferença entre o maior e o menor valor.
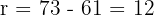
Variância
Calculamos a soma de  , dividimos por
, dividimos por  e subtraímos o quadrado da média aritmética
e subtraímos o quadrado da média aritmética  .
.

Desvio padrão
Calculamos a raiz quadrada da variância.

Calcule a média, a mediana e a moda da seguinte serie de números:

Vamos criar uma tabela com as colunas:
- Os valores da variável (
 ).
). - A frequência absoluta (
 ).
). - A frequência acumulada (
 ) para calcular a mediana.
) para calcular a mediana. - O produto da variável pela frequência absoluta (
 ) para calcular a média.
) para calcular a média.
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |
Moda
A moda é o valor que possui a maior frequência absoluta.
Observamos a coluna das  e verificamos que a maior frequência absoluta,
e verificamos que a maior frequência absoluta,  , corresponde a
, corresponde a  .
.
 .
.
Mediana
Para calcular a mediana, dividimos  por
por  e identificamos que a posição de
e identificamos que a posição de  na coluna de frequências acumuladas
na coluna de frequências acumuladas  corresponde a
corresponde a  .
.
 .
.
Média
Calculamos a soma do produto da variável pela sua frequência absoluta ( ), que resulta em
), que resulta em  , e dividimos pelo total
, e dividimos pelo total  .
.
 .
.
Faça o cálculo da variância e do desvio padrão dos números abaixo:

Primeiro, determinamos a média aritmética:
 .
.
Aplicamos a fórmula da variância:
 .
.
Por fim, calculamos a raiz quadrada do desvio padrão:
 .
.
Determine a média, mediana e moda da sequência de números:

Moda
A moda é  , pois é o valor que mais se repete.
, pois é o valor que mais se repete.
 .
.
Mediana
A série possui um número par de elementos, portanto, a mediana será a média entre os dois valores centrais.
 .
.
Média
Aplicamos a fórmula da média:
 .
.
Determine a média, a variância e o desvio padrão das seguintes sequências numéricas:
a. 
Média

Desvio médio

Variância
 .
.
Desvio padrão
 .
.
b. 
Média
 .
.

Variância

Desvio padrão
 .
.
Um teste foi aplicado em uma fábrica e essa foi a tabela obtida:
 | |
 |  |
 |  |
 |  |
 |  |
 |  |
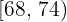 |  |
 |  |
Desenhe o histograma e o polígono de frequências acumuladas.
- Adicionamos uma nova coluna onde vamos colocar as frequências acumuladas (
 ):
): - Na primeira célula, colocamos a primeira frequência absoluta.
- Na segunda célula, somamos o valor da frequência acumulada anterior mais a frequência absoluta correspondente e assim sucessivamente até a última, que deve ser igual a
 .
.
 |  | |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
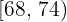 |  |  |
 |  |  |
 |
Considere as seguintes séries:
a) 
b) 
Calcule:
- A moda, a mediana e a média.
- O desvio médio, a variância e o desvio padrão.
- O quartil  e
e  .
.
- O decil  e
e  .
.
- O percentil  e
e  .
.
a. 
Moda
Não existe moda, pois todas as pontuações têm a mesma frequência.
Mediana
Ordenando os dados:
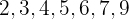
Portanto, a mediana é:
 .
.
Média

Variância

Desvio Padrão

Desvio Médio

Amplitude

Quartil 
Decil
A fórmula para posição dos decis é:

Sendo assim, os decis que estamos buscamos estão nas posições:

Percentil
A fórmula para a posição dos percentis é:

Portanto, os percentis que buscamos é dado nas posições:

b. 
Moda
Não existe moda, pois todas as pontuações têm a mesma frequência.
Mediana
Ordenando os dados:
latex]\displaystyle 1, 2, 3, 4, 5, 6, 7, 9.[/latex]
Portanto, a mediana é:
 .
.
Media
Variância

Desvio Padrão

Desvio Médio

Amplitude

Quartil
Decil
A fórmula para a posição dos decis é dada por:

Portanto, os decis que buscamos estão nas posições:

Percentil
A fórmula para a posição dos percentis é dada por:

Sendo assim, os percentis que buscamos estão nas posições:

Uma distribuição estatística é dada pela seguinte tabela
 | |
 |  |
 |  |
 |  |
 |  |
 |  |
Encontre:
- A moda, a mediana e a média.
- A amplitude, o desvio médio e a variância.
- Os quartis
 e
e  .
. - Os decis
 e
e 
- Os percentis
 e
e  .
.
Completamos a tabela com:
A frequência acumulada ( ) para calcular a mediana.
) para calcular a mediana.
O produto da variável pela sua frequência absoluta ( ) para calcular a média.
) para calcular a média.
A diferença em relação à média 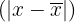 e seu produto pela frequência absoluta
e seu produto pela frequência absoluta 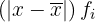 para calcular o desvio médio.
para calcular o desvio médio.
O produto do quadrado da variável pela sua frequência absoluta (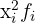 ) para calcular a variância e o desvio padrão.
) para calcular a variância e o desvio padrão.
 |  |  |  |  | 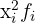 | |
 |  |  |  |  |  |  |
 |  |  |  |  |  |  |
 |  |  |  |  |  |  |
 |  |  |  |  |  |  |
 |  |  |  |  |  |  |
 |  |  |  |
Moda
Primeiro, identificamos o intervalo onde se encontra a moda, que será aquele com a maior frequência absoluta ( ).
).
A classe modal é:  .
.
Aplicamos a fórmula para o cálculo da moda para dados agrupados, extraindo os seguintes dados:
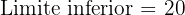 .
.
 .
.
 .
.
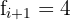 .
.
 .
.

Mediana
Para encontrar o intervalo da mediana, dividimos  por
por  , pois a mediana representa o valor central:
, pois a mediana representa o valor central:
 .
.
Buscamos na coluna das frequências acumuladas ( ) o intervalo que contém
) o intervalo que contém  .
.
Classe da mediana:  .
.
Aplicamos a fórmula para o cálculo da mediana para dados agrupados, extraindo os seguintes dados:
 .
.
 .
.
 .
.
 .
.
 .
.
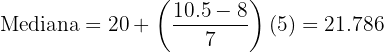 .
.
Média
Calculamos a soma do produto da variável por sua frequência absoluta ( ), que é
), que é  , e dividimos por
, e dividimos por  :
:
 .
.
Desvio médio
Calculamos a soma dos produtos das diferenças absolutas em relação à média pelas respectivas frequências absolutas  , que é
, que é  , e dividimos por
, e dividimos por  :
:
 .
.
Variância
Calculamos a soma de  , dividimos por
, dividimos por  e subtraímos o quadrado da média aritmética,
e subtraímos o quadrado da média aritmética,  :
:
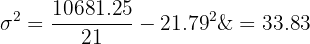
Considerando a distribuição estatística:
 | |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
Encontre:
- A mediana e a moda.
- Quartil


 e
e 

 .
. - Média.
Ampliamos a tabela com outra coluna onde dispomos a frequência acumulada 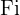

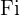 :
:
Na primeira célula, colocamos a primeira frequência absoluta.
Na segunda célula, somamos o valor da frequência acumulada anterior à frequência absoluta correspondente e assim sucessivamente até a última, que deve ser igual a 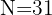

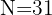 .
.
 |  |  | |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  | |
 |
Moda
Primeiramente, buscamos o intervalo onde se encontra a moda, que será o intervalo com a maior frequência absoluta ( ).
).
A classe modal é:  .
.
Aplicamos a fórmula para o cálculo da moda para dados agrupados, extraindo os seguintes dados:
Limite inferior:  .
.





Mediana
Buscamos o intervalo onde se encontra a mediana. Para isso, dividimos  por
por  , pois a mediana é o valor central:
, pois a mediana é o valor central:

Buscamos na coluna das frequências acumuladas ( ) o intervalo que contém
) o intervalo que contém  .
.
Classe da mediana:  .
.
Aplicamos a fórmula para o cálculo da mediana para dados agrupados, extraindo os seguintes dados:





Quartis
Cálculo do primeiro quartil
Buscamos o intervalo onde se encontra o primeiro quartil, multiplicando  por
por  e dividindo por
e dividindo por  :
:

Buscamos na coluna das frequências acumuladas ( ) o intervalo que contém
) o intervalo que contém  .
.
A classe de  é:
é:  .
.
Aplicamos a fórmula para o cálculo dos quartis para dados agrupados, extraindo os seguintes dados:





Cálculo do terceiro quartil
Buscamos o intervalo onde se encontra o terceiro quartil, multiplicando  por
por  e dividindo por
e dividindo por  :
:

Buscamos na coluna das frequências acumuladas ( ) o intervalo que contém
) o intervalo que contém  .
.
A classe de  é:
é:  .
.
Aplicamos a fórmula para o cálculo dos quartis para dados agrupados, extraindo os seguintes dados:





Média
Não é possível calcular a média, pois não se pode determinar a marca de classe do último intervalo.
Resumir com IA:


